容器是应用走向云端之后必然的发展趋势，因此笔者非常乐于和大家分享我们这段时间对容器的理解、心得和实践。

本篇教程持续编写了2个星期左右，只是为了大家更好地了解、理解和消化这个技术，能够搭上这波车。

你可以关注我们的公众号“magiccodes”给我们留言，也可以加入我们的QQ群（85318032）一起讨论，我们希望能够多多交流，多多分享。

如果觉得不错，请多多点赞或者请我们喝杯咖啡，你们的支持是我们前进的最大动力！

目

录

Docker和ASP.NET Core

Docker 正在逐渐成为容器行业的事实标准，受到 Windows 和 Linux 生态系统领域最重要供应商的支持。 （Microsoft 是支持 Docker 的主要云供应商之一。）现在，Docker 基本上已经在各大云或本地的任何数据中心普及了。

如何将.NET程序托管到Docker之中，相信这是广大.NET开发者的一个疑问。事实上，.NET Framework 支持在Docker中运行，但是仅能在windows 容器中运行，这并不符合我们的预期，因此，本篇我们只侧重于讨论ASP.NET Core和Docker。

在使用之前，笔者还是有必要介绍下ASP.NET Core。如果您对此非常熟悉和了解或者对此节不感兴趣，可以跳过本节。

ASP.NET Core简介

ASP.NET Core是一个跨平台的高性能开源框架，用于生成基于云且连接 Internet 的新式应用程序。使用 ASP.NET Core，我们可以：

• 建置 Web 应用程序和服务、IoT 应用和移动后端。

• 能够在 Windows、macOS 和 Linux 上进行开发和运行。部署到云或本地。

• 在 .NET Core 或 .NET Framework 上运行。

• 能够在 IIS、Nginx、Apache、Docker 上进行托管或在自己的进程中进行自托管我们的应用。

性能是.NET Core的一个关键特性，这里有必要介绍下。在这块，我们摘取了一份社区的测试汇总统计，仅供参考：

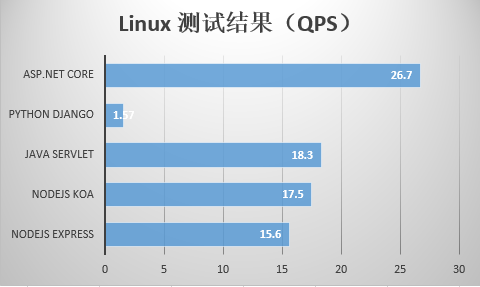
具体过程大家可以访问此链接来查看详情：

https://www.cnblogs.com/savorboard/archive/2016/10/17/dotnet-benchmarks.html

ASP.NET Core和Docker

刚才说了这么多，我们回到主题。.NET Core天生就为跨平台设计，并且和Docker搭配非常友好，而且微软官方在这块提供了很多支持。比如说：

• 轻量

• 跨平台，天生对Linux友好

• 模块化

• 提供了轻量型容器镜像

• 高性能（领先于Java servlets、Go 和 node.js）

接下来，我们一起来了解官方镜像。ASP.NET Core的官方镜像名称为microsoft/aspnetcore，微软针对Docker上的 ASP.NET Core 应用进行了优化，因此容器可以更快启动。为开发人员生成Docker镜像时，Microsoft 侧重于提供了以下主要方案：

1. 用于开发和生成 .NET Core 应用的镜像。

2. 用于运行 .NET Core 应用的镜像。

为什么是多个镜像？因为在开发、生成和运行容器化应用程序时，通常具有不同的优先级。 通过为这些单独的任务提供不同的镜像，有助于独立优化开发、生成和部署应用程序的过程。在开发期间，我们侧重的是开发更改的速度以及调试的能力。在生产环境，我们侧重的是应用部署和容器启动的速度和效率。

这里我们顺便提下我们基于.NET Core 2.1开发的免费开源框架——Magicodes.Admin，其demo现在已经完全托管在Docker之中，部署在腾讯云的容器服务之中，大家可以点击访问测试下速度和稳定性，启动速度这点没得说。推荐访问Https地址，因域名在备案之中，http域名可能无法访问。

Magicodes.Admin开源库地址：https://gitee.com/xl_wenqiang/Magicodes.Admin.Core

Demo地址：https://demoadmin.xin-lai.com

Admin

123456abcD

在本篇Docker教程中，我们会结合Magicodes.Admin的实践进行讲解，同时我们也会尽量提供一些实践案例分享给大家，比如Magicodes.Admin demo、Magicodes云服务、小程序商城（即将开源）、爱车APP等Docker完整托管案例，以便大家更易于理解和使用Docker。在Magicodes.Admin框架中，接口服务使用.NET Core 2.1开发，在docker上基于microsoft/dotnet:2.1-aspnetcore-runtime镜像使用Kestrel web服务器，后台前端使用Angular开发，在docker上基于nginx镜像使用nginx服务器进行托管，并启用了HTTPS支持和GZIP压缩。

我们回过来继续。.NET镜像 (microsoft/dotnet) 同样适用于基于 .NET Core 的控制台应用。使用 Docker 和 .NET Core非常适用于生产部署和托管，主要有以下几点：

• 无需本地安装——可以直接使用 .NET Framework，而无需本地安装。只下载相关的Docker 镜像，其中包含 .NET Framework。

• 在容器中开发——你可以在一致的环境中开发，使开发和生产环境类似（可避免一些问题，例如开发人员计算机上的全局状态）。 通过VS的一些扩展插件，我们甚至可以直接从 Visual Studio 启动容器。

• 容器中测试——可以在容器中测试，减少由于环境配置不当或上次测试遗留的其他更改而导致的故障。

• 在容器中生成——可以在容器中生成代码。

• 在所有环境中部署——可以通过你的所有环境部署镜像。 这种方法减少了配置差异导致的故障，通常通过外部配置（例如，注入的环境变量）改变镜像行为。

注意：

Docker 镜像容器可以在 Linux 和 Windows 上本机运行。 但是，Windows 镜像仅能在 Windows 主机上运行，Linux 镜像可以在 Linux 主机和 Windows 主机上运行（到目前为止，使用 Hyper-V Linux VM），其中主机是指服务器或 VM。

注意：

.NET Framework也可以使用Docker进行托管，不过仅能托管到windows容器之中。

在具体应用和实践之前，我们有必要了解以下内容。

Kestrel

Kestrel是一个基于libuv的跨平台ASP.NET Core web服务器，libuv是一个跨平台的异步I/O库。ASP.NET Core模板项目使用Kestrel作为默认的web服务器。

Kestrel支持以下功能：

• HTTPS

• 用于启用不透明升级的WebSockets

• 位于Nginx之后的高性能Unix sockets

Kestrel 被.NET Core支持的所有平台和版本所支持。Kestrel 可以单独使用，也可以与反向代理服务器（如 IIS、Nginx 或 Apache）一起使用。 反向代理服务器接收到来自 Internet 的 HTTP 请求，并在进行一些初步处理后将这些请求转发到 Kestrel。

在没有 Kestrel 或自定义服务器实现的情况下，不能使用 IIS、Nginx 和 Apache。 ASP.NET Core 设计为在其自己的进程中运行，以实现跨平台统一操作。 IIS、Nginx 和 Apache 规定自己的启动过程和环境。 若要直接使用这些服务器技术，ASP.NET Core 必须满足每个服务器的需求。 使用 Kestrel 等 Web 服务器实现时，ASP.NET Core 可以控制托管在不同服务器技术上的启动过程和环境。

注意：

Kestrel 可以单独使用，也可以与反向代理服务器（如 IIS、Nginx 或 Apache）一起使用。在docker容器中，我们推荐使用Kestrel。

在大部分情况下，我们推荐使用反向代理服务器。主要是有以下好处：

• 可以限制所承载的应用中的公开的公共外围应用。

• 可以提供额外的配置和防护层。

• 可以更好地与现有基础结构集成。

• 可以简化负载均衡和 SSL 配置。 仅反向代理服务器需要 SSL 证书，并且该服务器可使用普通 HTTP 在内部网络上与应用服务器通信。

说了这么多，总归还是“纸上得来终觉浅，绝知此事要躬行”。我们来一起实践：

首先我们需要安装以下包：

Install-Package Microsoft.AspNetCore.Server.Kestrel -Version 2.1.3

然后就可以编写启动代码：

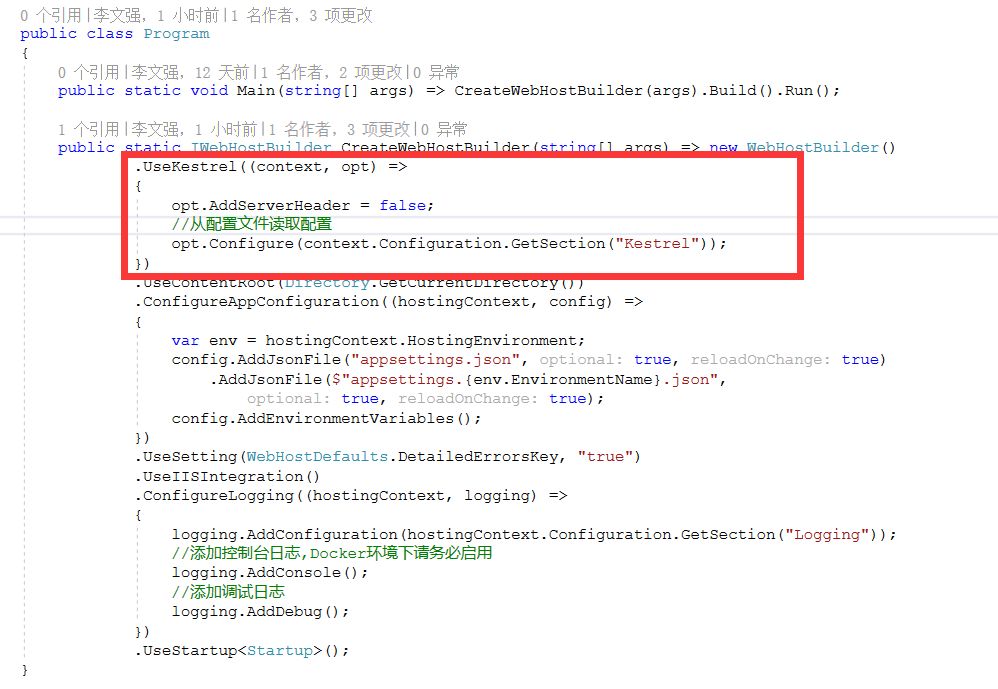
在上面的代码中，我们通过了配置文件来配置Kestrel，我们也推荐大家使用配置文件来配置Kestrel。相关配置Demo如下：

当然，我们也可以通过代码来配置kestrel：

按环境加载配置

ASP.NET Core 基于使用环境变量的运行时环境配置应用行为。ASP.NET Core 在应用启动时读取环境变量ASPNETCORE_ENVIRONMENT，并将该值存储在 IHostingEnvironment.EnvironmentName 中。 ASPNETCORE_ENVIRONMENT 可设置为任意值，但框架支持三个值：Development、Staging 和 Production。 如果未设置 ASPNETCORE_ENVIRONMENT，则默认为 Production。

注意：

在Docker容器中，我们经常会修改ASPNETCORE_ENVIRONMENT环境变量来模拟开发、测试和生产环境。

因此在代码中，我们可以根据环境变量来启用或关闭相应的功能，其中场景最广泛的一点是——根据不同的环境加载不同的配置。同时，内置的环境变量配置提供程序（EnvironmentVariablesConfigurationProvider）还可以在运行时从环境变量键值对加载配置。具体见以下代码：

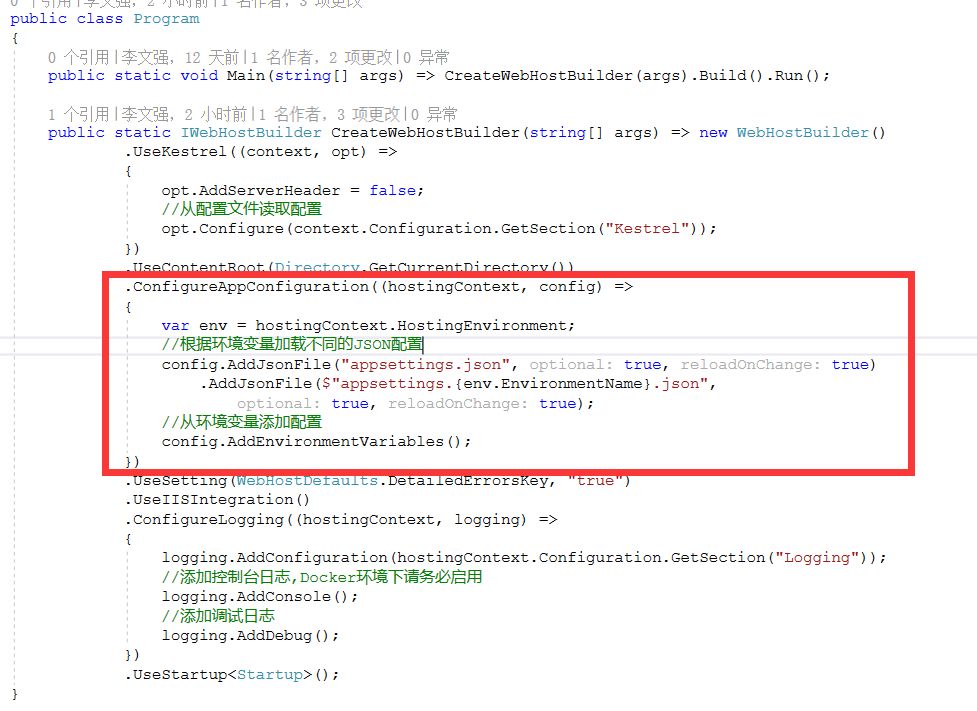
内置的日志记录提供程序

ASP.NET Core 提供以下内置日志记录提供程序，在很多情况下，对我们会很有帮助：

• 控制台日志提供程序

• 调试日志提供程序

• EventSource日志提供程序

• EventLog日志提供程序

控制台日志提供程序

在Docker环境下，为了便于排错，我们推荐启用此日志提供程序。在平常的情况下，我们通过控制台运行程序（比如通过dotnet run运行）也会输出控制台日志。在使用之前，需要安装以下包：

Install-Package Microsoft.Extensions.Logging.Console -Version 2.1.1

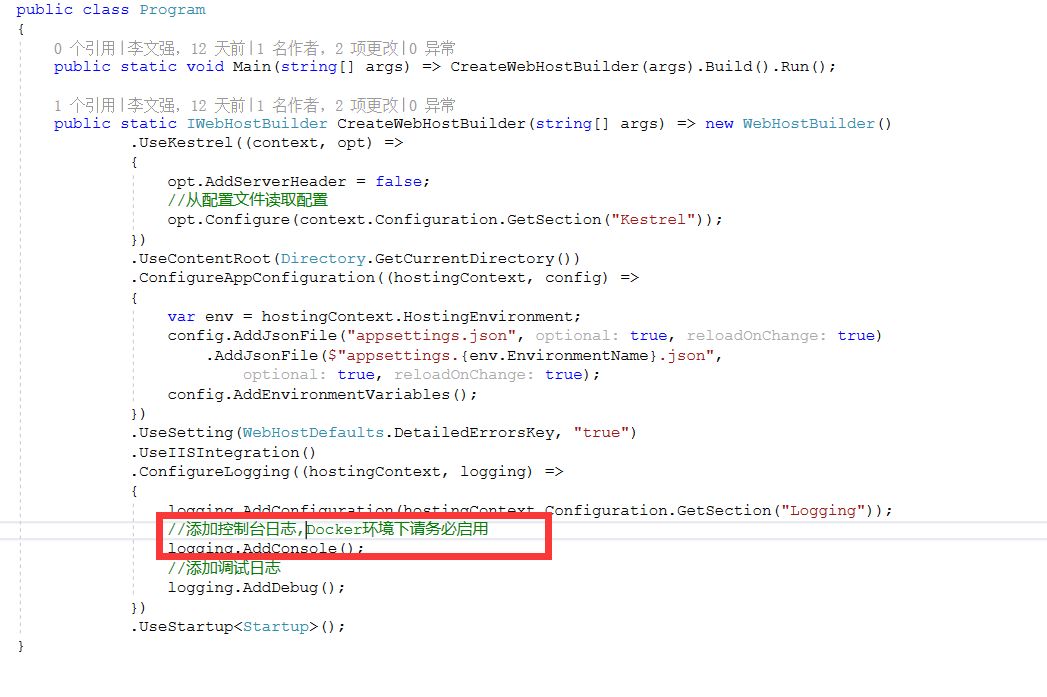
然后我们可以在代码中通过以下代码启用：

logging.AddConsole();

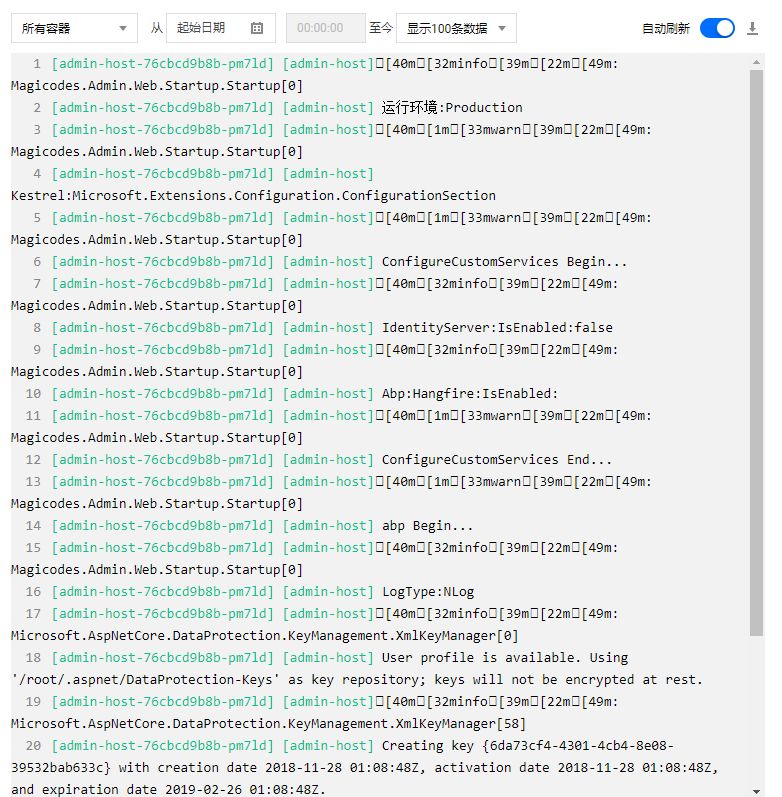
完整代码如图所示：

添加了之后，我们在云端的容器服务的日志中，就可以看到控制台日志了。下面以腾讯云容器服务为例。首先打开腾讯云【容器服务】的【服务】页面，如图所示：

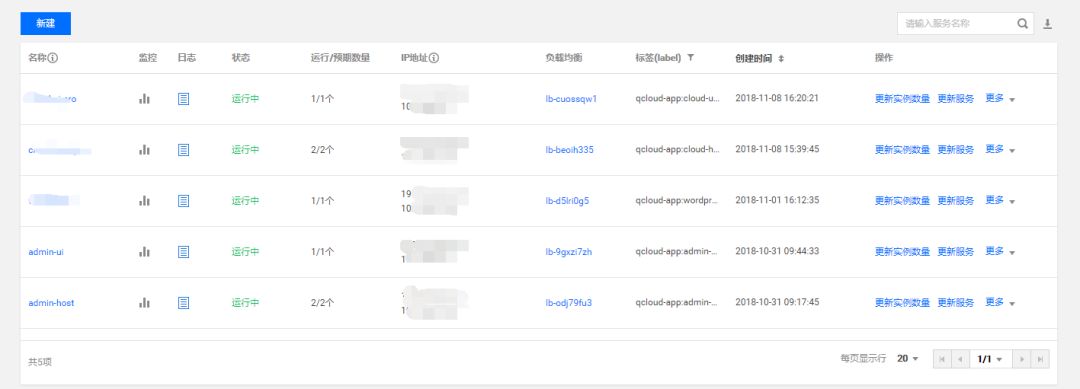
我们可以点击【日志】操作按钮的图标来查看日志：

我们也可以点击具体的某个实例来查看相关日志，这里就不多写了。

注意：

通过控制台日志，我们可以输出一些启动信息以用来做启动诊断，同时我们也可以根据控制台日志来查看请求状况和运行状况。

调试日志提供程序

和控制台日志一样，也需要安装相关依赖包：

Install-Package Microsoft.Extensions.Logging.Debug -Version 2.1.1

该包使用 System.Diagnostics.Debug 类（Debug.WriteLine 方法调用）来写入日志输出。注意，在 Linux 中，此提供程序将日志写入 /var/log/message。

代码启用方式如下所示：

logging.AddDebug();

EventSource日志提供程序

包依赖关系如下：

Install-Package Microsoft.Extensions.Logging.EventSource -Version 2.1.1

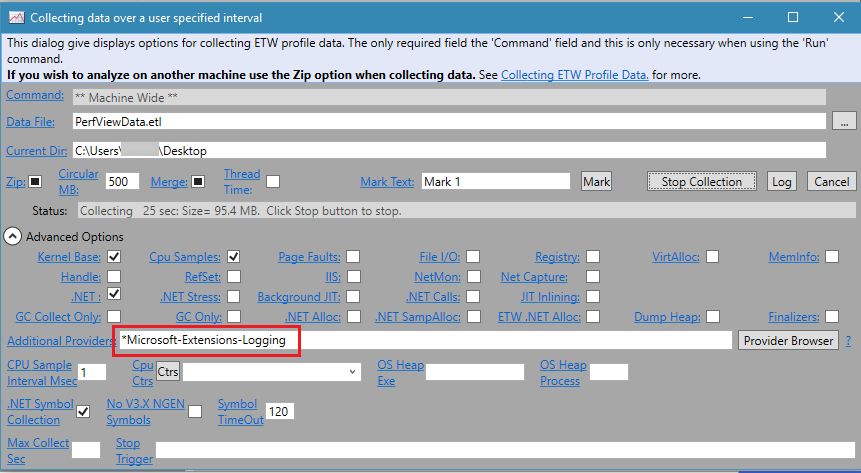
该提供程序可实现事件跟踪。不过值得注意的是，该提供程序尚无支持 Linux 或 macOS 的事件集合和显示工具。期待官方提供相关工具。

而在windows server，可以通过开源工具https://github.com/Microsoft/perfview来收集和查看日志，如下图所示：

EventLog日志提供程序

需要添加包：Microsoft.Extensions.Logging.EventLog。

主要用于向 Windows 事件日志发送日志输出。

关于ASP.NET Core的相关内容，我们先介绍到这里。接下来我们主要是围绕Docker开发工作流程在进行讲解。

搭建并使用Docker

Docker的安装非常简单，我们这里仅以windows 10操作系统（推荐）为例进行讲解。

安装Docker

这里以Docker for windows为例，其他环境请参考官网教程。

注意：

不推荐使用Docker Toolbox，Docker Toolbox适用于较旧的Mac和Windows系统。

要安装 Docker，请先查看用于 Windows 的 Docker：安装须知了解相关信息。

安装须知链接：https://docs.docker.com/docker-for-windows/install/#what-to-know-before-you-install

注意：

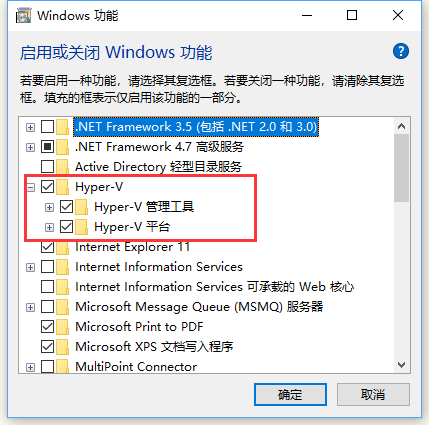
使用Docker for windows需要启用Hyper-V功能。以下是系统要求：

• Windows 10 64位：Pro，Enterprise或Education（Build 14393或更高版本）。

• 在BIOS中启用虚拟化。通常，默认情况下启用虚拟化。这与启用Hyper-V不同。

• 支持CPU SLAT的功能。

• 至少4GB的RAM。

Docker for Windows安装包括：安装提供 Docker Engine，Docker CLI客户端，Docker Compose，Docker Machine和 Kitematic。

安装包下载链接：https://store.docker.com/editions/community/docker-ce-desktop-windows

参考：https://docs.docker.com/docker-for-windows/

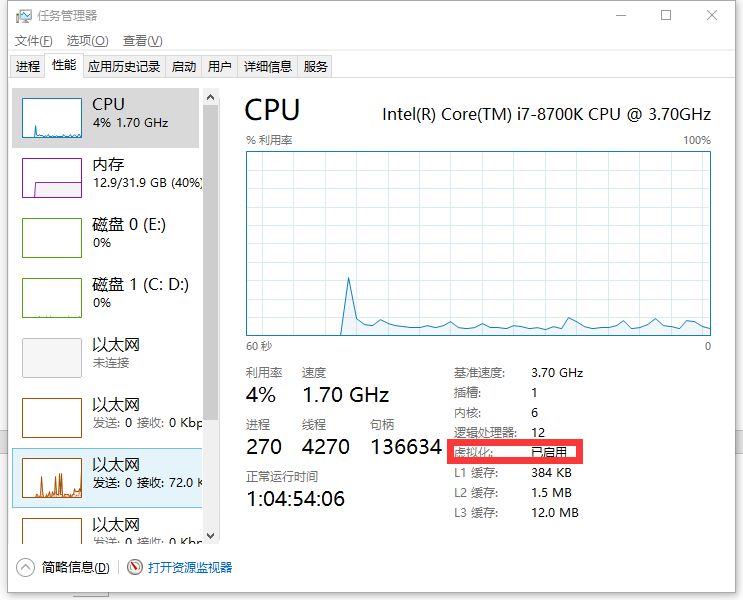
安装完后，会提示点击重启电脑。重启后会自动启动Docker程序，如果弹出下图所示提示，则需要在Windows 功能中启用Hyper-V功能和 在BIOS CPU配置中打开 “虚拟化配置”，打开之后，如下图所示，虚拟化会显示已启用。反之安装成功。

注意虚拟化已启用，如下图所示（这里秀一把我NB的台式机，是不是比你们的服务器都高端N个档次）：

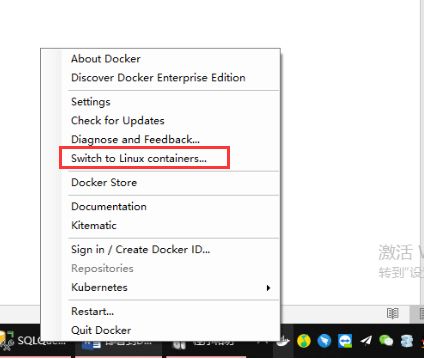
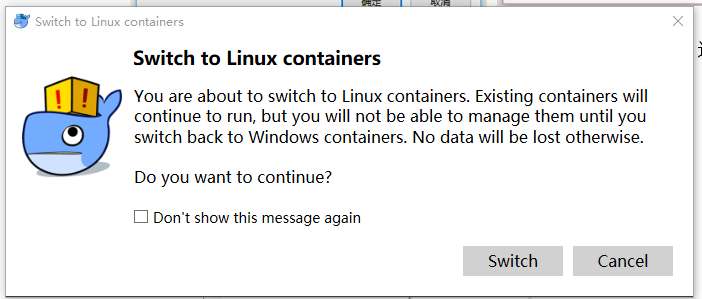
以上配置完成后我们推荐将docker容器切换到Linux环境，选择右下角Docker图标右键选择” Switch to Linux containers”进行切换，如果显示” Switch to Windows containers”则已处于Linux容器。

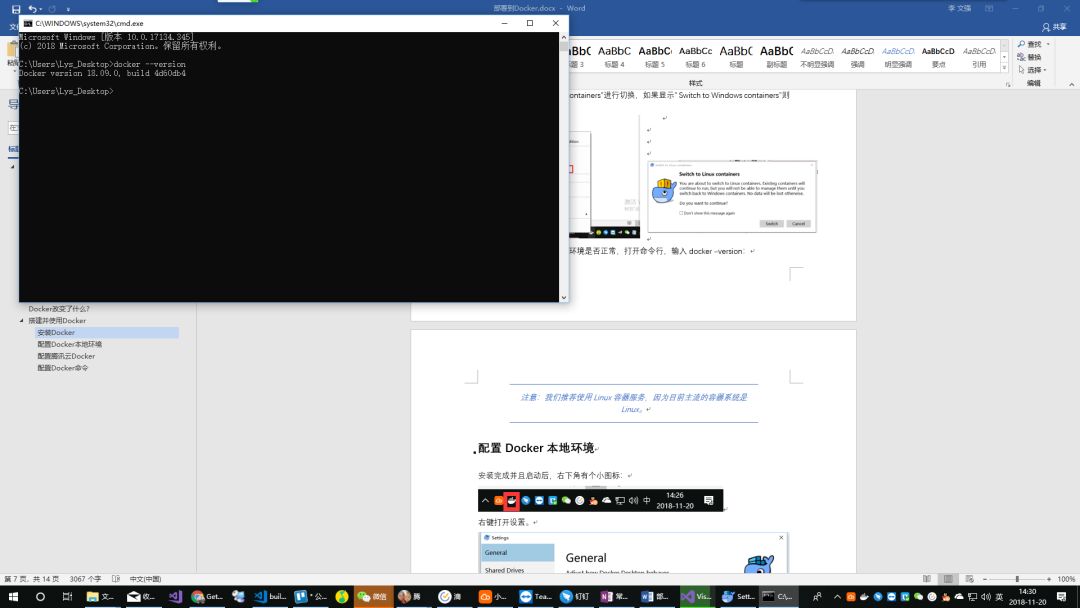
这是我们可以测试Docker环境是否正常，打开命令行，输入docker –version：

注意：

我们推荐使用Linux容器服务，因为目前主流的容器系统是Linux，并且从资源的利用来说，Linux可以让资源得到更大的利用。

关于docker的安装和配置，这里不再细说，大家可以关注我们的公众号“magiccodes“来查阅相关的教程以及录屏。

配置Docker本地环境

安装完成并且启动后，右下角有个小图标：

右键打开设置。

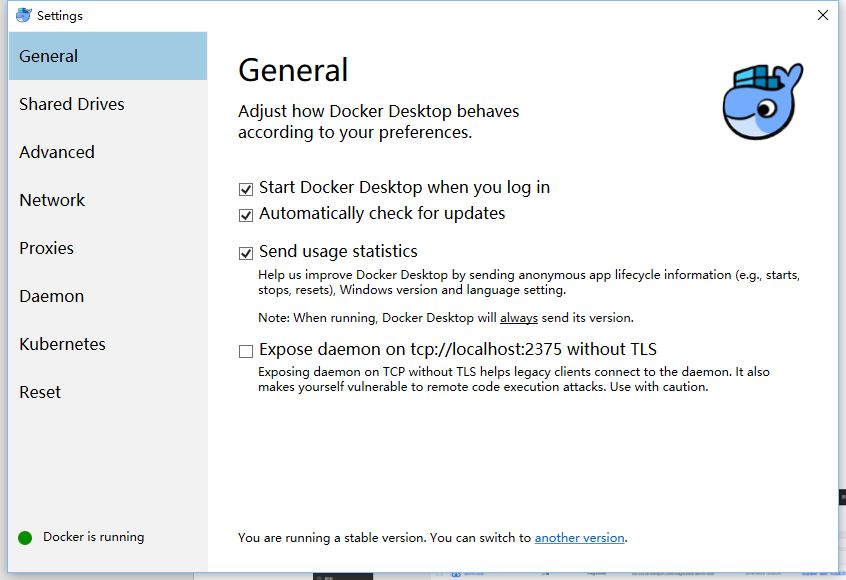
Docker for Windows 中的共享驱动器必须配置为支持卷映射和调试。右键单击系统托盘中的 Docker 图标，单击“设置”，然后选择“共享驱动器”。 选择 Docker 存储文件的驱动器。 单击“应用”。

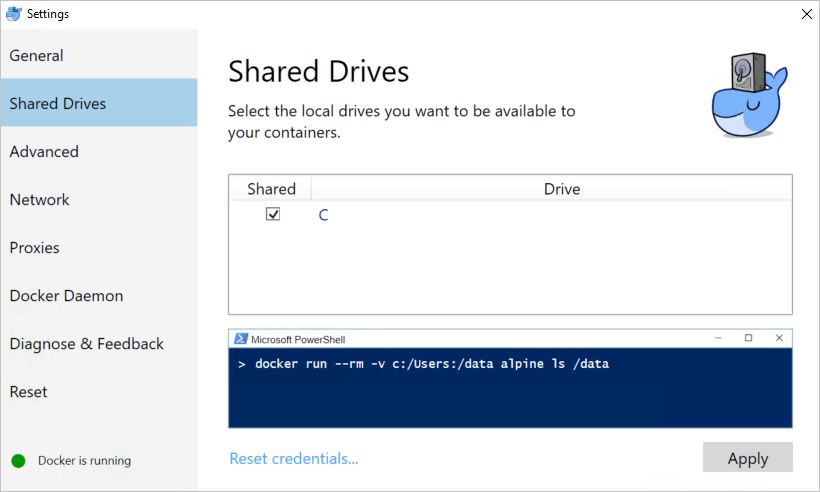
其他的配置我们这里就不多说了，具体见公众号“magiccodes”中提供的录屏教程。

运行一个简单的demo

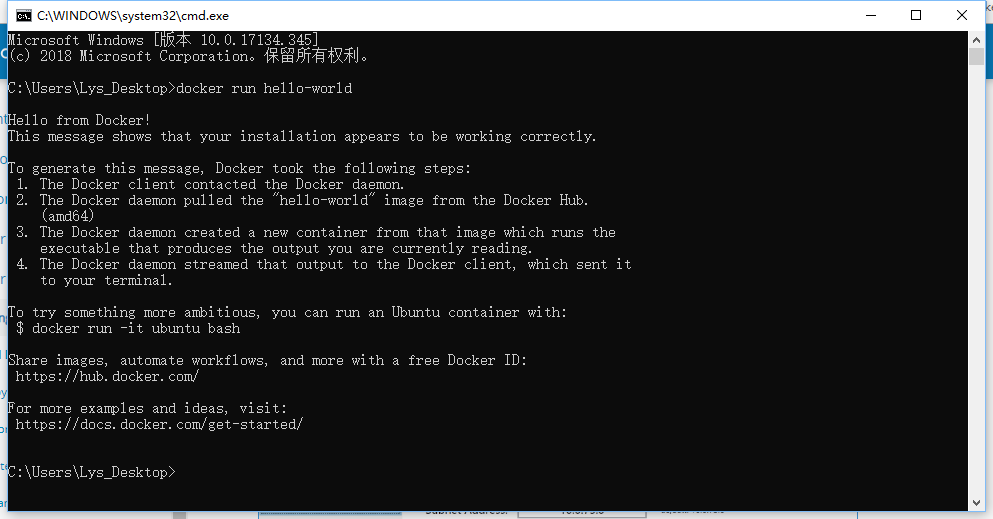
我们先运行官方的Hello world示例：

docker run hello-world

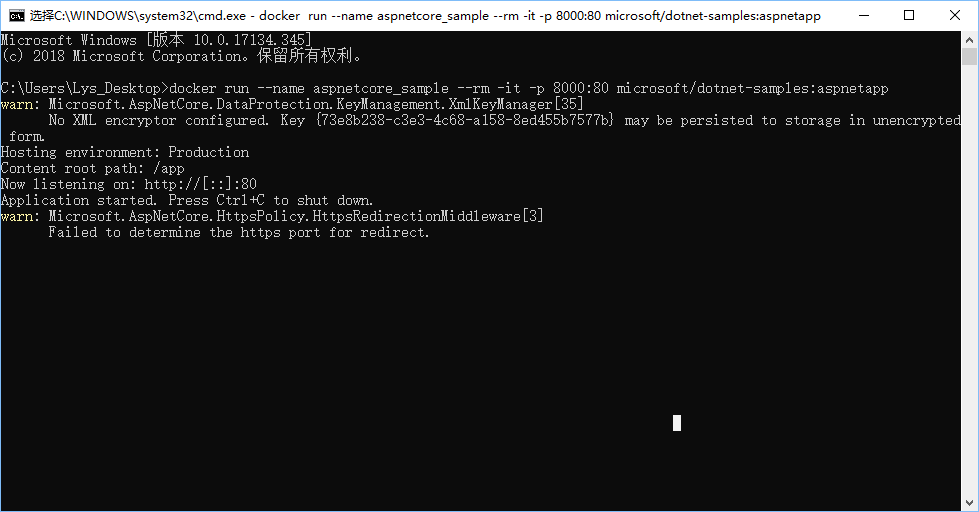
我们也可以简单运行一个web示例，比如：

docker run --name aspnetcore_sample --rm -it -p 8000:80 microsoft/dotnet-samples:aspnetapp

应用程序启动后，使用浏览器打开http://localhost:8000，即可看到以下界面：

Docker的安装和配置在Windows 10操作系统下非常简单，我们也极力推荐大家使用此环境。毕竟，一个好的开发环境可以大大提高大家的使用和开发效率。

前期内容：

Docker最全教程——从理论到实战（一）

Docker最全教程——从理论到实战（二）

长按识别二维码，了解更多精彩内容

如果喜欢作者的文章，请关注“magiccodes”订阅号以便第一时间获得最新内容。本文版权归作者和湖南心莱信息科技有限公司共有，欢迎转载，但未经作者同意必须保留此段声明，且在文章页面明显位置给出原文连接，否则保留追究法律责任的权利。

QQ群：

编程交流群<85318032> 

产品交流群<897857351>