边缘化搭建 DotNet Core 2.1 自动化发布和部署(下)

写在前面

　　本篇文章是上一篇边缘化搭建 DotNet Core 2.1 自动化发布和部署(上)的后续操作，本文主要讲解如何开启Docker Remote API，开启Remote API后的权限安全问题。配置Jenkins构建项目，并在云服务器上构建成功。废话不多说，我们一起来动手操作吧。

先决条件

1.一台Debain 9系统 x86 服务器硬件环境：1核2G 40G硬盘。

2. x86服务器成功安装并运行Docker环境（本文不阐述安装过程，读者可查阅参考文献）

2.根据上一篇边缘化搭建 DotNet Core 2.1 自动化发布和部署(上)搭建好的边缘计算环境

开启Docker Remote API

　　Remote API主要用于远程访问Docker守护进程从而下达指令的。因此，我们在启动Docker守护进程时，需要添加-H参数并指定开启的访问端口。通常，我们可以通过编辑守护进程的配置文件来实现。不过对于不同操作系统而言，守护进程启动的配置文件也不尽相同。但是现在我们不需要去改动系统原有的配置文件，通过drop-in file方式进行覆盖配置，所以在不改动系统配置文件的方式下，我们的覆盖配置文件的路径基本保持一致。

创建 override.conf

　　我们需要在x86服务器上创建 override.conf 配置文件。

$ mkdir -p /etc/systemd/system/docker.service.d/$ nano override.conf

编辑 override.conf

　　1.将以下内容加入到override.conf文件

[Service]
ExecStart=ExecStart=/usr/bin/dockerd -H fd:// -H tcp://0.0.0.0:2376

　　2.重启Docker服务

$ sudo systemctl daemon-reload
$ sudo systemctl restart docker.service

测试Remote API

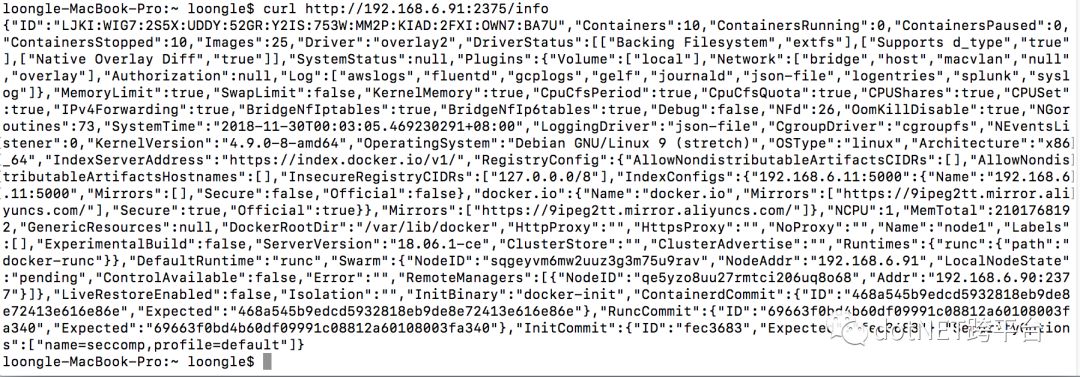
$ curl http://your ip:2375/info

　　测试成功将返回如下信息：

640?wx_fmt=png

开启 Remote API 安全认证

　　到目前位置，我们已经在x86服务器开启Docker Remote API来控制Docker服务。但是，细心的读者应该已经发现，在这个连接访问的过程中并没有安全认证机制，也就是说任何人只要知道Remote API地址和端口都可以控制Docker 服务，然而这样将会大大增加了服务的风险。接下来笔者将告诉大家如何为Remote API添加认证机制。

生成证书

　　1.新建一个命名为 createSSL.sh 的 Shell 脚本文件。

$ sudo nano createSSL.sh

　　2.在 createSSL.sh 文件中加入以下代码：

640?wx_fmt=png

3.执行生成证书操作。

$ sh createSSL.sh master

　　第一个ca-key.perm 生成时可能需要你输入一个密码，随便就可以了，只要记得住。此处略有坑，不能一路回车，$VAR 输入的参数必须是域名，这波操作是在配置jenkins docker插件时发现的。笔者使用的域名是：master ，为了各位读者能顺利进行教程操作，请跟笔者一起使用相同的域名。

配置 override.conf

　　1.将生成的ca.pem, server-cert.pem, server-key.pem 文件复制到 /root/.docker 目录下。当然此目录并非固定的，读者可以根据自己的心情来存放其他的目录路径。目录存放的路径绝对不能错，否者docker.service 将会启动不了。

$ mkdir -p /root/.docker
$ cp {ca,server-cert,server-key}.pem /root/.docker/

　　2.最终 /etc/systemd/system/docker.service.d/override.conf 文件内容如下：

[Service]
ExecStart=ExecStart=/usr/bin/dockerd -H unix:///var/run/docker.sock -D -H tcp://0.0.0.0:2376 --tlsverify --tlscacert=/root/.docker/ca.pem --tlscert=/root/.docker/server-cert.pem --tlskey=/root/.docker/server-key.pem

　　3.重启Docker服务

$ sudo systemctl daemon-reload
$ sudo systemctl restart docker.service

测试 Remote API 安全认证

　　测试的使用记得一定要使用域名进行访问，如果没有设置域名解析，可以通过修改本地的host的方式进行实现。

curl https://master:2376/info --cert /root/master/cert.pem --key /root/master/key.pem --cacert /root/master/ca.pem

创建Jenkins项目

　　接下来，我们进入使用树莓派搭建好的Jenkins系统新建项目，并通过 docker-compose 方式启动项目。Let's do it

下载证书

　　通过SSH连接树莓派后，将x86服务器上生成的 ca.pem，server-cert.pem，server-key.pem 证书下载到树莓派 /var/jenkins_home/cert/master 目录。

$ sudo mkdir -p /var/jenkins_home/cert/master
$ sudo scp rtdsoft@192.168.6.200:/home/loongle/master/{cert,key,ca}.pem /var/jenkins_home/cert/master

新建任务

　　1.构建一个自由风格的软件项目

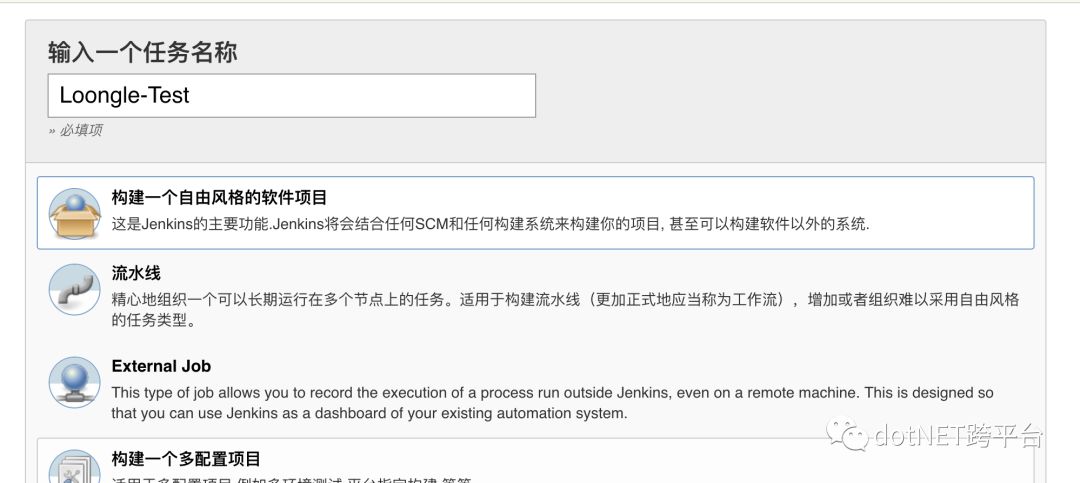
640?wx_fmt=png

　　2.设置源码地址，为了方便各位读者，笔者已经新建一个项目代码仓，读者可以直接使用这个仓，快速跑一遍流程。git 地址：https://gitee.com/wenalu/Rpi-MvcTest.git

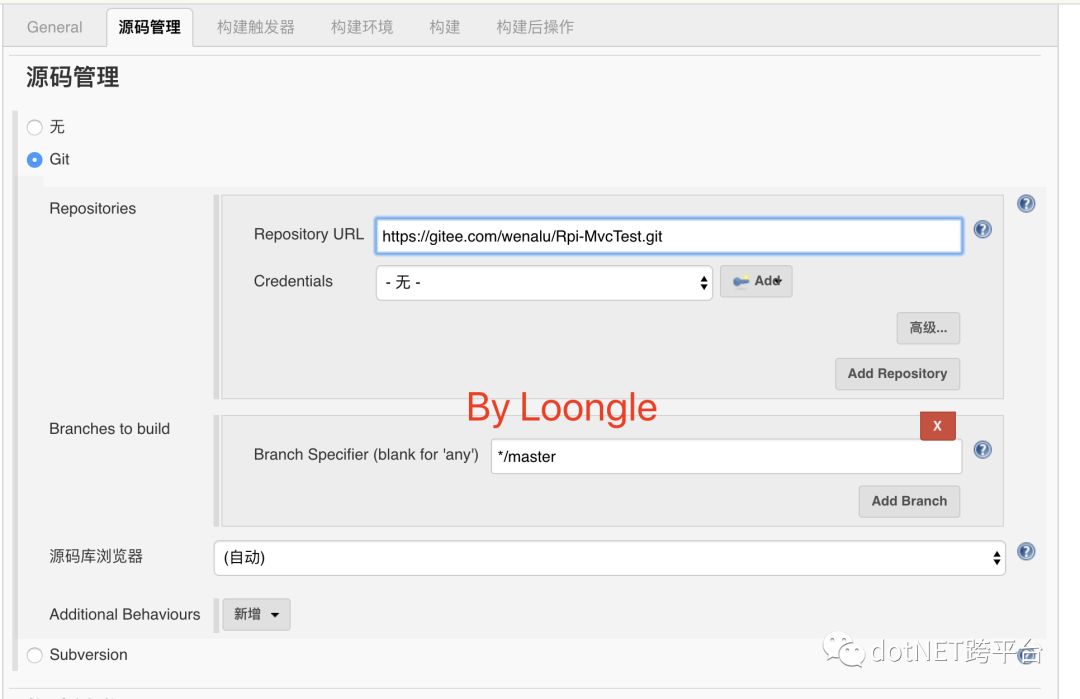
640?wx_fmt=png

　　3.设置构建触发器，让项目可以定时轮询仓库，执行自动构建，本次配置的参数为2分钟获取一次。

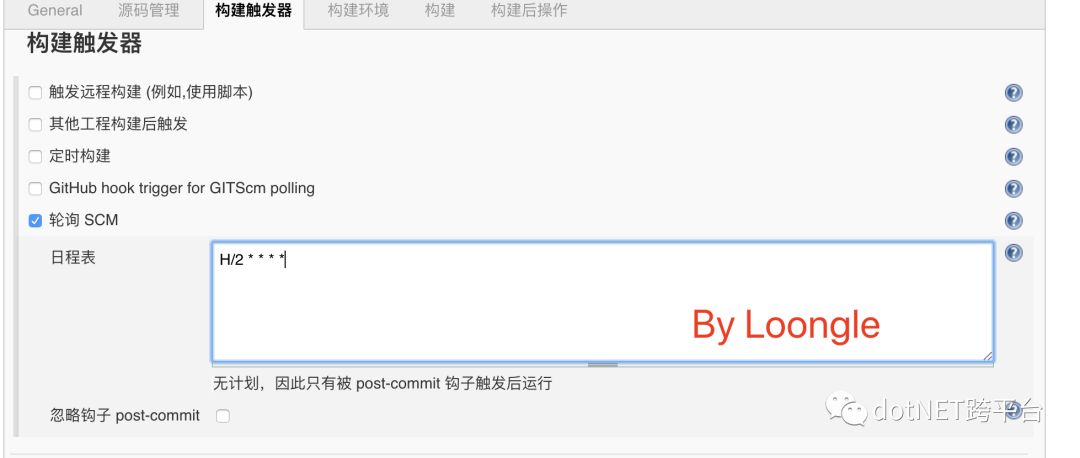
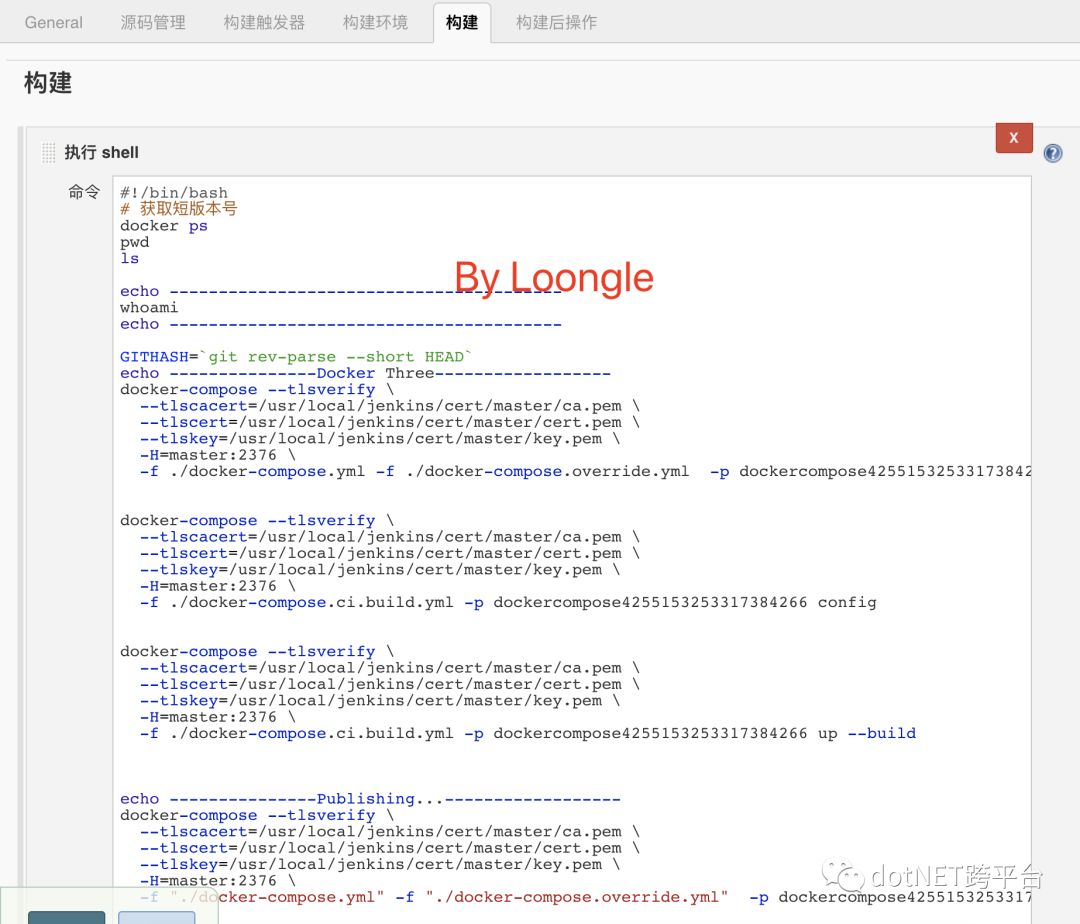
640?wx_fmt=png

　　4.新增构建，选择执行Shell，并填写以下脚本内容

640?wx_fmt=png

注意事项

　　请各位读者在填写执行Shell内容时注意 -H=master:2376 ，master的含义是生成证书使用的域名，亦是在上篇博文中，启动 Jenkins 添加 --add-host 解析参数，笔者填写的解析IP：192.168.6.200，所以最后笔者访问master将会指向6.200的机器。当然，读者若使用的是云服务器，并且配置了域名解析，那么只需要将 master 改成解析的域名即可，不需要在启动 Jenkins 添加 --add-host 参数。请各位读者谨记，避免踩坑。为了方便各位读者，重贴启动 Jenkins 代码，请按需修改启动参数。

$ sudo docker run --name=jenkins --restart=always --add-host master:192.168.6.200 -p 8080:8080 -p 50000:50000 -v /var/run/docker.sock:/var/run/docker.sock -v $(which docker):/bin/docker -v /var/jenkins_home:/usr/local/jenkins/ -d auto-jenkins

测试

　　当各位读者的构建结果最后输出的信息最终和笔者保持一致的时候，那么整个流程就跑完了。

640?wx_fmt=png

写在后面

　　至此，本篇内容已经全部完毕了，博文中可能有很多表述不太专业的地方，还请各位读者指点交流。其实本文章标题有另外一个《「穷」式搭建 DotNet Core 2.1 自动化发布和部署》，后来考虑很久不用这个标题是因为本身自己属于这个行业的专业人士，不能用比较庸俗的词来表述这篇文章，所以才有现在的这个标题。很开心我终于写完了，写这一大章的内容真的挺不容易，也挺佩服那些坚持下来，写了那么多博文的作者是怎么走过来的。为他们对社区作出的贡献喝彩吧。大吉大利，今晚吃鸡