默认模板之缺
在工作学习中,我们经常需要创建一些简单的控制台应用(Console App)去验证某个想法,或者作为小工具交付给其他同事。
通常我们的选择是 Visual Studio 自带的 Console App 模板,这个经典模板只有预设好的 csproj 文件和空荡荡的 Main 方法,偶尔还会附送一行 Console.WriteLine("Hello World!");,除此之外没有任何附加功能。
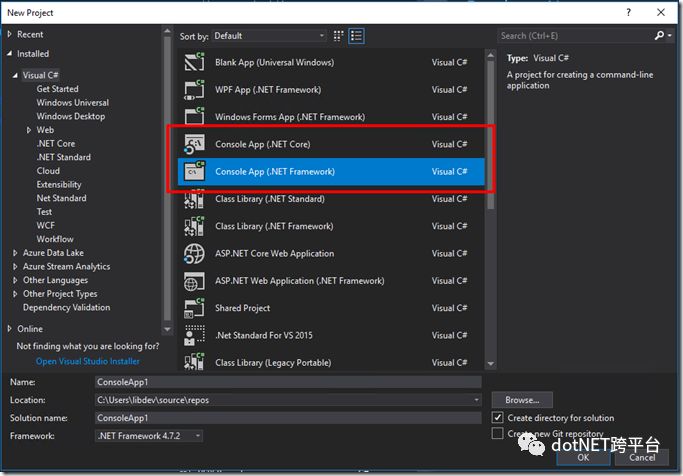
代码看起来大概是这样——
using System;
namespace ConsoleApp1
{class Program
{static void Main(string[] args)
{ Console.WriteLine("Hello World!");}
}
}
面对这如同白纸一样的模板,如果我们需要捕捉一下异常、调用一下异步方法、记录一下log呢?勤奋的你一定存有一些常用的经典代码片段和配置文件吧,那就一一复制进来呗……折腾了十来分钟后,终于可以开始写代码了……
N天之后,又需要新写个控制台应用了,我们再次重复一遍上述过程。
安装模板插件
受到 HTML5 Boilerplate 的启发,Visual Studio Marketplace 上也出现了一款叫做 C# Console App Boilerplate 的插件,顾名思义,就是在默认 Console App 模板基础上添加常用特性以解决痒点。
可以从 Visual Studio Marketplace 上直接下载 vsix 文件安装:https://marketplace.visualstudio.com/items?itemName=vej.20181111
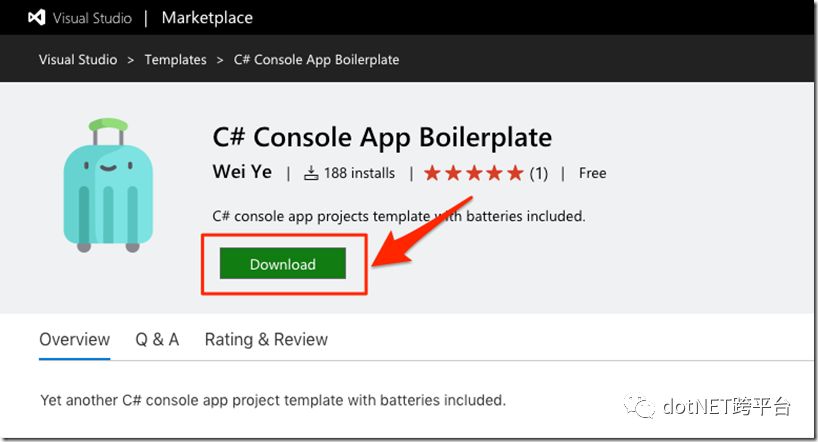
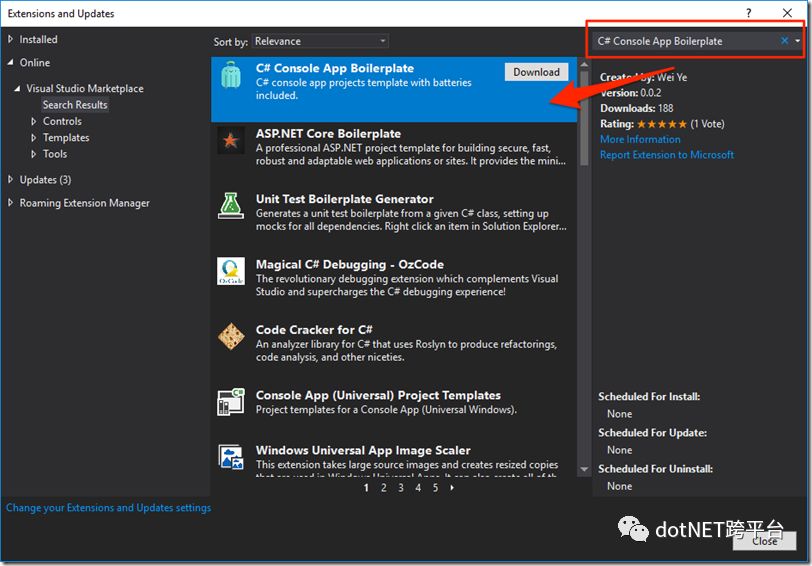
也可以在 Visual Studio 2017 的 Extensions and Updates 中输入 C# Console App Boilerplate 搜索并安装:
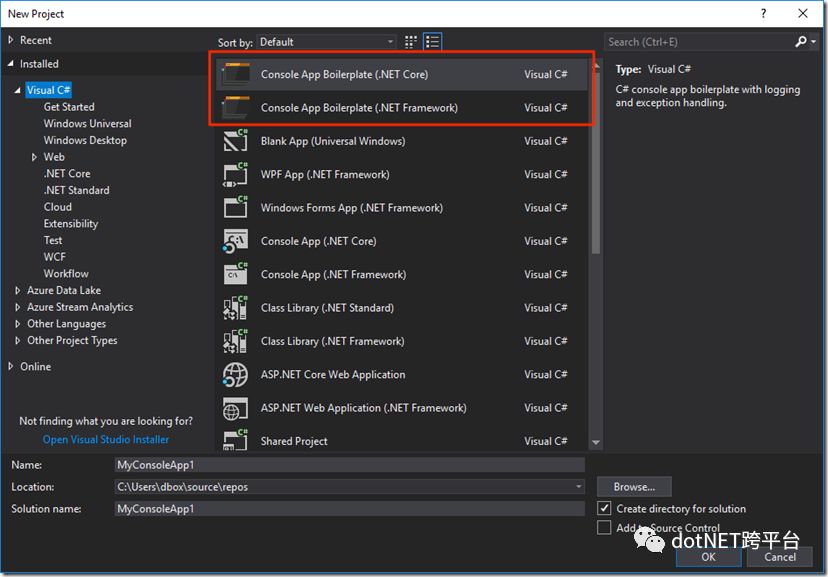
安装完成后,通过 Visual Studio 再次新建 Project 时,就可以在 Visual C# 分类下找到 Console App Boilerplate 的两个新模板。
模板便利特性
通过 Console App Boilerplate 模板新建 Project 后,我们可以看到编辑器窗口中默认打开的 Main.cs 文件——
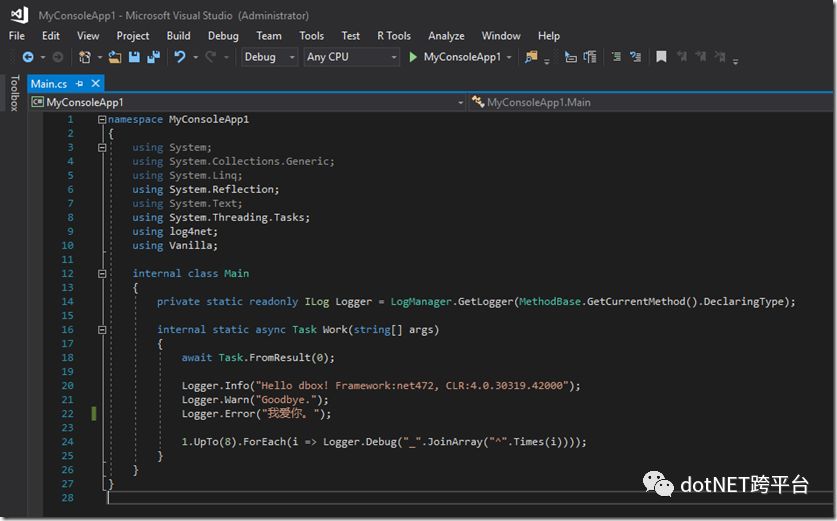
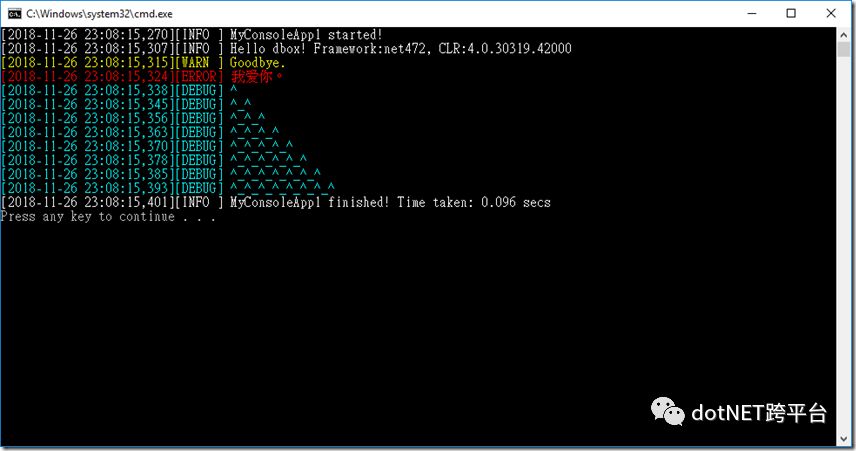
我们可以直接运行样例代码,也可以将 Work 方法中样例代码替换成我们的业务逻辑。样例代码直接运行的效果如下——
同样是控制台应用,那么它和经典的 Console App 模板究竟有何不同呢?我们打开 Program.cs 文件便可知晓——
使用了 C# 7.1 中新引入的异步
Main方法,用来放置业务逻辑的Work方法同样是异步的。调用异步方法时,可以直接使用await关键字,省去了我们之前在同步Main方法中做同样操作时附加的.Wait()甚至是.ConfigureAwait(false).GetAwaiter().GetResult()的繁琐。预设的 log4net 配置了 RollingFileAppender 和 ColoredConsoleAppender 两个 Appender,前者可以在日志文件中额外记录下机器名称、进程的名称和 ID,后者确保在跨平台环境下日志依然“出彩”。
整体的异常处理,针对
AggregateException和Exception分别进行了捕捉和记录,并依此设置了 Exit Code。Stopwatch测量整体的运行时间并在最后一行日志中输出。修改代码页以支持 UTF-8 字符正常显示,如果需要显示汉字,在非中文的 Windows 中还需要额外地将 cmd.exe 的默认字体设置为 MingLiU / 新细明体 或其他CJK字体。
此外,无论是 .NET Core 还是 .NET Framework 版本的 csproj 文件都采用了 MSBuild 15.0 新引入的 project SDK 格式。新的格式不仅更简单清爽,也带来了很多方便的特性,这里不再赘述。
相关需求解法
在模板的基础上,如果需要解析复杂的命令行参数,可以考虑引入 NuGet 包 CommandLine.Net 进行解析。它的使用方法非常简单,GitHub 项目的一页 README 便已阐述清楚,亦支持跨平台。
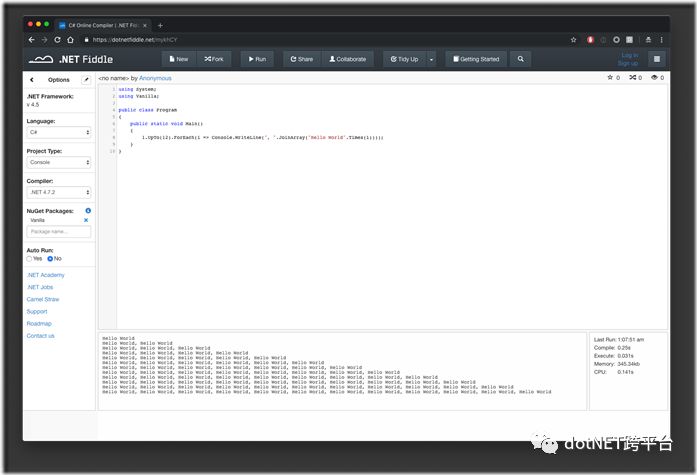
反之,如果仅仅想运行几行代码,又不愿等 Visual Studio 启动呢?可以用浏览器打开 .NET Fiddle 直接尝试,它不仅支持最新的 .NET Framework 4.7.2 版本,还可以选择 Roslyn 2.0,而且在 C# 之外支持 F# 和 VB.NET。
.NET社区新闻,深度好文,欢迎访问公众号文章汇总 http://www.csharpkit.com


)
![P3224 [HNOI2012]永无乡(并查集+权值线段树合并/平衡树)](http://pic.xiahunao.cn/P3224 [HNOI2012]永无乡(并查集+权值线段树合并/平衡树))
![牛客题霸 [没有重复项数字的所有排列] C++题解/答案](http://pic.xiahunao.cn/牛客题霸 [没有重复项数字的所有排列] C++题解/答案)

)
![P7599-[APIO2021]雨林跳跃【二分,倍增,ST表】](http://pic.xiahunao.cn/P7599-[APIO2021]雨林跳跃【二分,倍增,ST表】)
- 网络选拔赛 GCD on Sequence(线段树))
![牛客题霸 [ 验证IP地址] C++题解/答案](http://pic.xiahunao.cn/牛客题霸 [ 验证IP地址] C++题解/答案)
)
)
![P4332-[SHOI2014]三叉神经树【LCT】](http://pic.xiahunao.cn/P4332-[SHOI2014]三叉神经树【LCT】)
![牛客题霸 [ 环形链表的约瑟夫问题] C++题解/答案](http://pic.xiahunao.cn/牛客题霸 [ 环形链表的约瑟夫问题] C++题解/答案)
)
)

![P7405-[JOI 2021 Final]雪玉【二分】](http://pic.xiahunao.cn/P7405-[JOI 2021 Final]雪玉【二分】)
![牛客题霸 [ 集合的所有子集] C++题解/答案](http://pic.xiahunao.cn/牛客题霸 [ 集合的所有子集] C++题解/答案)
I love max and multiply(转化))
