本篇教程持续编写了3个星期左右并且一直在完善、补充具体的细节和实践,预计全部完成需要1到2个月的时间。由于编写的过程中极其费时,并且还需要配合做一些实践(有些实践存在一些坑,而且极其费时费事)。因此目前产出的速度已经跟不上发布的速度了,后续的发布节奏会放慢,请大家多多理解和多多包含。
在这个过程中,我们希望能够多多交流,多多分享。根据目前和大家的交流,笔者针对大家的情况进行了一些修改和补充,希望对大家有所帮助。另外,对于熟悉容器服务的你,也可以参与进来,让我们一起打造这个系列教程,以帮助更多的人。同时,我们也希望得到大家的支持,请多多点赞或者请我们喝杯咖啡,你们的支持是我们前进的最大动力!
目录




运行 Docker 应用程序
如果应用程序只有一个容器,则可通过将其部署到 Docker 主机(虚拟机或物理服务器)来运行该程序。 但如果应用程序包含多项服务,则可使用单个 CLI 命令 (docker-compose up) 或使用 Visual Studio(会在其中使用该命令)将其部署为组合应用程序。
单个应用,就如我们上面的demo :
docker run --name aspnetcore_sample --rm -it -p 8000:80 microsoft/dotnet-samples:aspnetapp
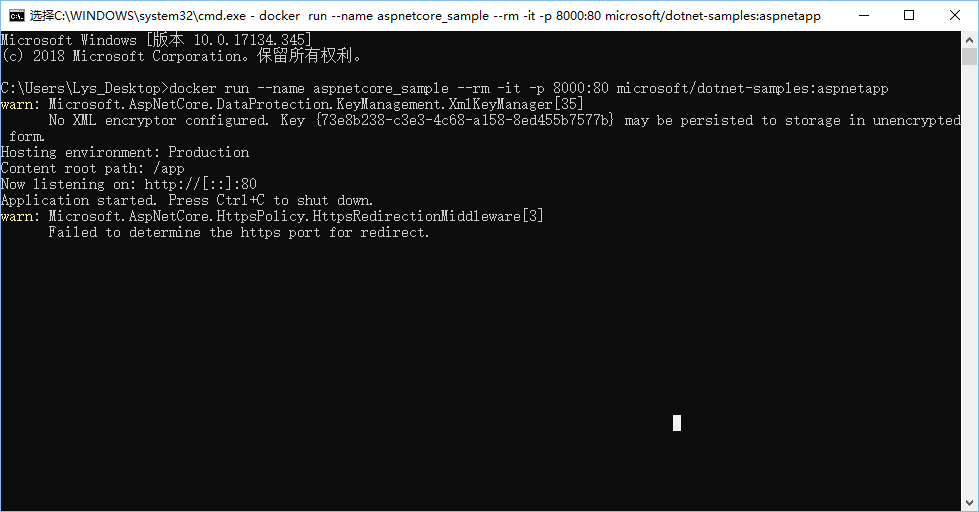
应用程序启动后,使用浏览器打开http://localhost:8000,即可看到以下界面:
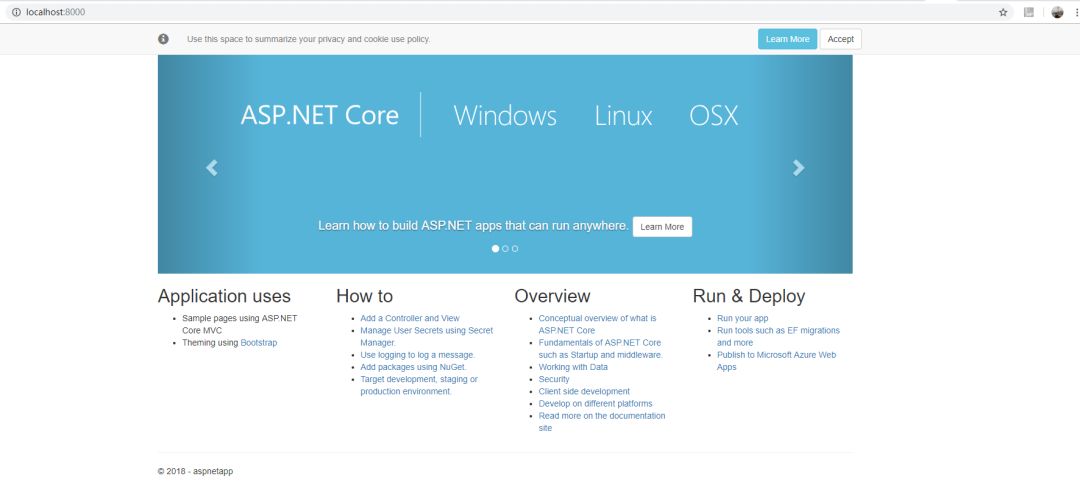
但是如Magicodes.Admin框架所示,有后台接口、后台前端应用、前端接口、小程序端、APP等等,那么我们可以通过上面配置的docker-compose文件来部署为组合应用程序。执行起来很简单,只需要运行以下命令:
docker-compose up
执行之后,我们可以看到:
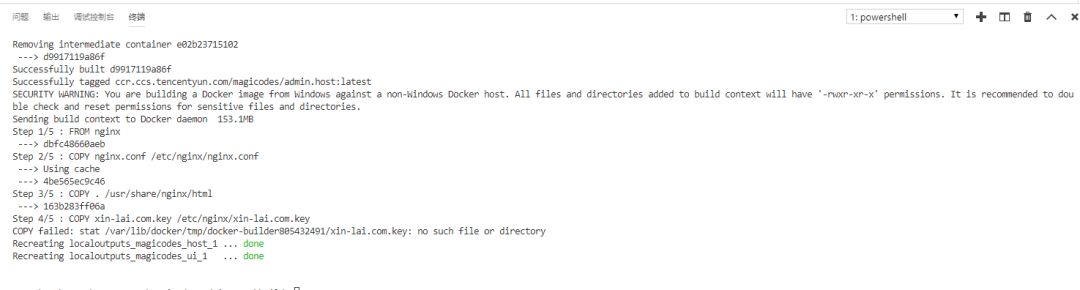
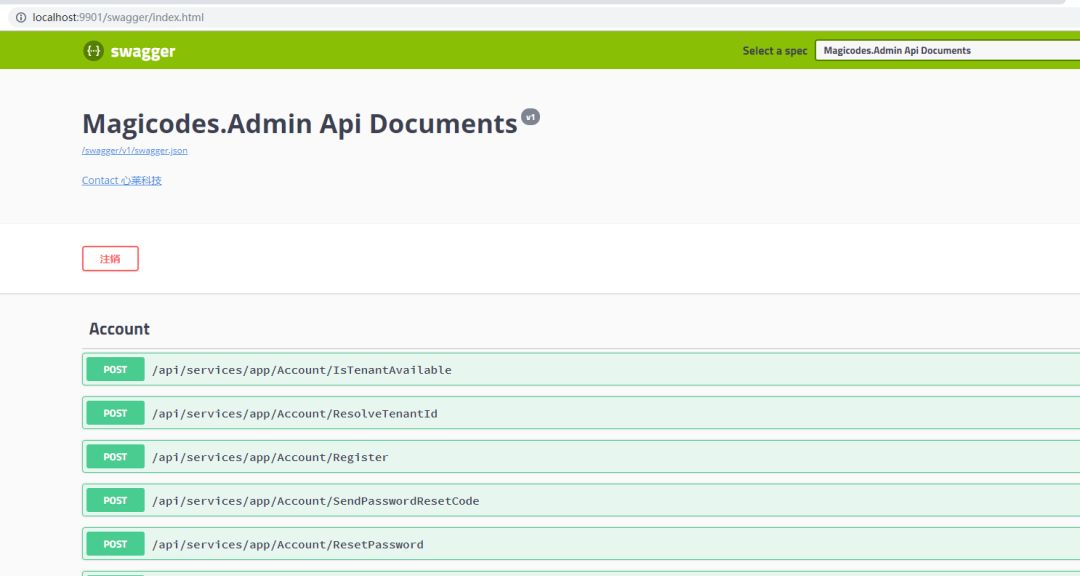
Magicodes.Admin提供了本地编译、打包、构建镜像以及运行等整套脚本,在通常情况,我们仅需一键运行脚本即可。
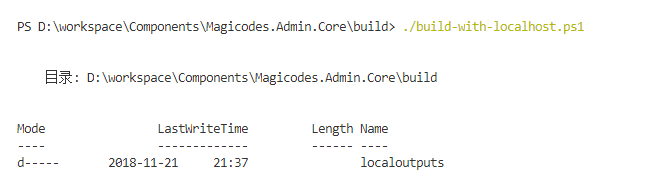
脚本会自动完成对后台服务和前端应用的构建以及运行。在上一节中,我们说到,Visual Studio对这块已经完成了相关的支持,如果是使用Visual Studio的开发者,仅需按下F5即可运行。

测试
容器正常运行了,我们可以让测试人员来访问我们的服务来进行相关的功能测试和可用性测试。当然,我们也可以编写自定义脚本进行自动化测试,就如前面章节中Docker-compose常用场景中提到的自动化测试环境:
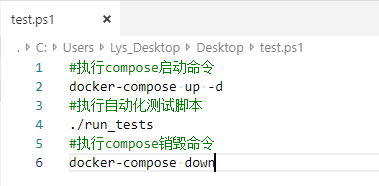
部署或继续开发
开发完成后,我们就需要部署我们的应用,并且继续项目迭代。在部署之前,我们需要推送我们的镜像,比如使用docker push命令,我们可以将镜像推送到docker的官方镜像库,也可以推送到各大云自己的镜像库,然后再通过docker pull命令拉取镜像进行部署。同时,也可以使用一些CI(持续集成)工具来完成自动化的边开发边部署的工作。CI这块,我们接下来会介绍基于Azure DevOps、Tencent hub、Jenkins以及TeamCity等服务或工具来完成CI。在本节,我们继续了解镜像推送的语法:
docker push {镜像名称}:{镜像版本}
在推送之前,我们需要登录到一个镜像仓库,如果未指定镜像仓库地址,默认为官方仓库 Docker Hub。相关语法如下所示:
docker login --username {用户名} --password {密码} {仓库地址}
推送成功之后,如下所示:
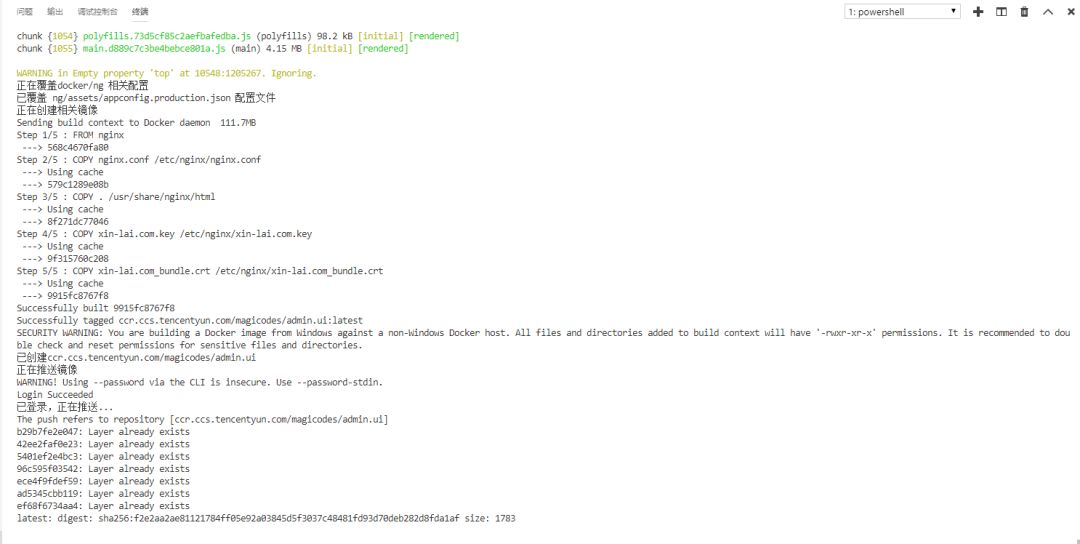
关于部署和托管这块,接下来我们以腾讯云的容器服务进行举例。
为什么是腾讯云,因为他家的创业服务支持活动赞助了我们很多代金券,基本上接近免费,因此从成本考虑,我们首选腾讯云(腾讯云:瞎说什么大实话)。

部署完成之后,我们可以继续产品或项目的迭代。在整个开发工作流中,我们可以显著的看到,由于Docker的出现,在一定层次上改变了我们的工作和交付流程,并且可以大大的简化CI、CD流程。或者就从构建上来说,配置dockerfile来完成构建,比传统的方式来的迅猛多了。而配置docker-compose.yml一次启动多个服务,简直是分布式架构、微服务架构开发和测试人员的福音。
至此,整个Docker持续开发工作流程就到此结束,在后面的篇幅,我们侧重于从实战的角度来讲解这些内容。
使用Kitematic来管理docker容器
这里,我们先插播一个内容。本节,我们先来介绍下Kitematic。
Kitematic是一个开源项目,旨在简化在Mac或Windows PC上使用Docker的过程。Kitematic自动化Docker安装和设置过程,并提供直观的图形用户界面(GUI)来运行Docker容器。
因此,我们推荐大家使用Kitematic工具来查看和管理自己的容器服务,如果尚未安装此工具,大家可以通过以下方式进行安装:
从Docker for Mac或Docker for Windows菜单中选择Kitematic,开始使用Kitematic安装。如下图所示:
直接从Kitematic版本页面下载Kitematic 。下载地址:https://github.com/docker/kitematic/releases/
注意:这里我们不推荐使用Docker Toolbox,原因我们在前面已经说过,Docker Toolbox仅支持老版本的操作系统,属于过时的工具。
安装完成之后,启动后可以看到如下界面:
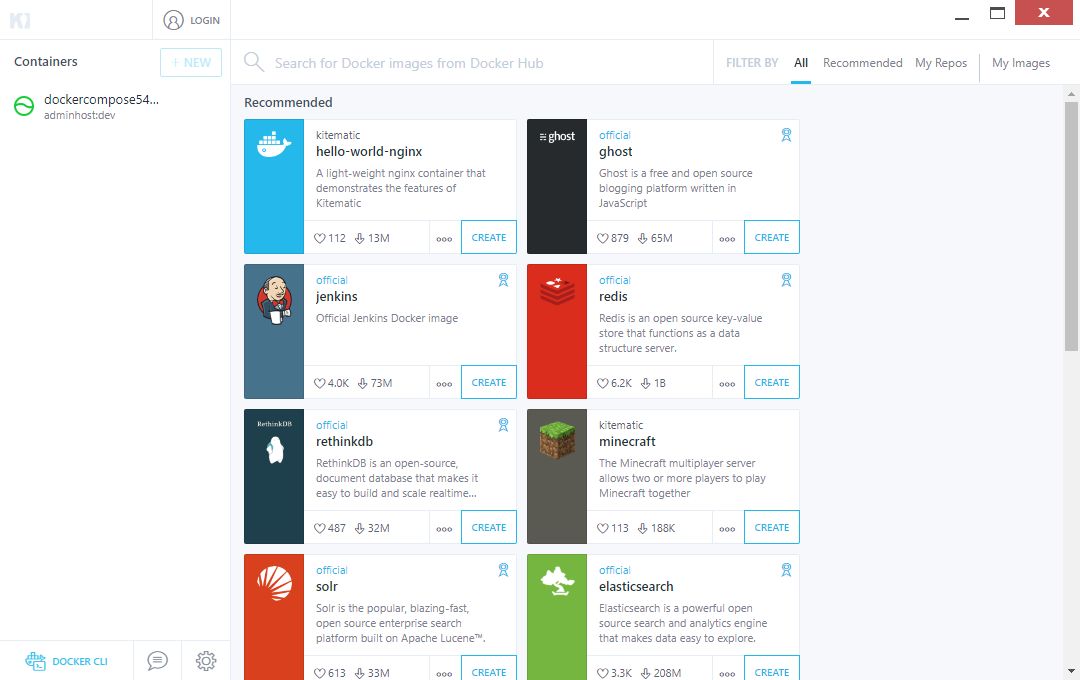
也可以点击某个服务来查看详情、相关设置、日志等:
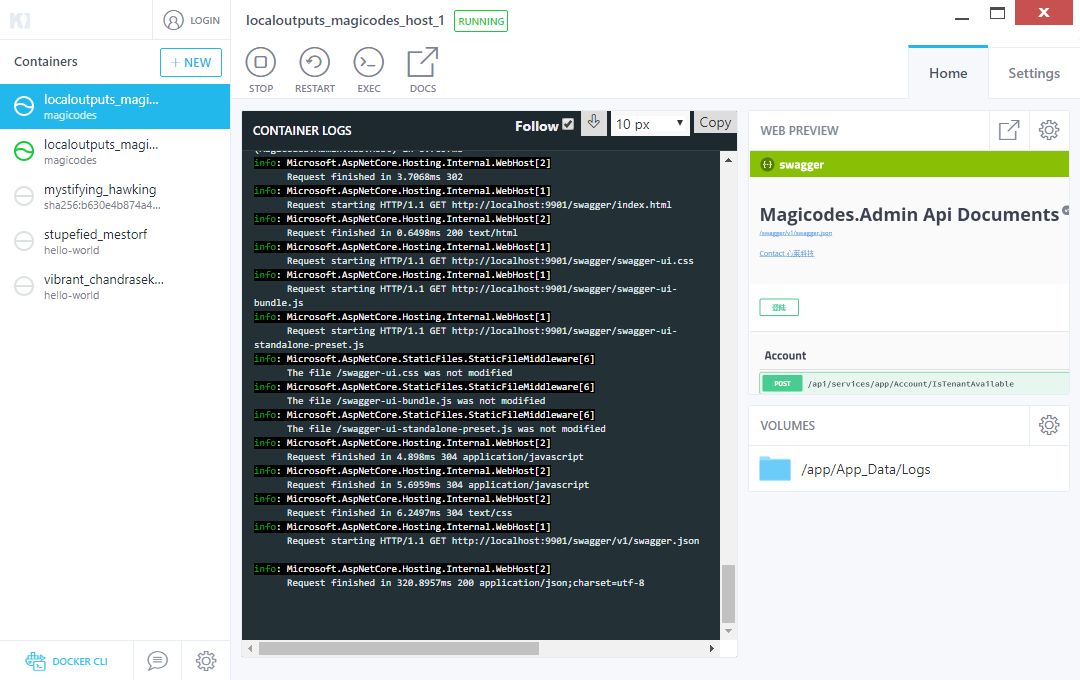
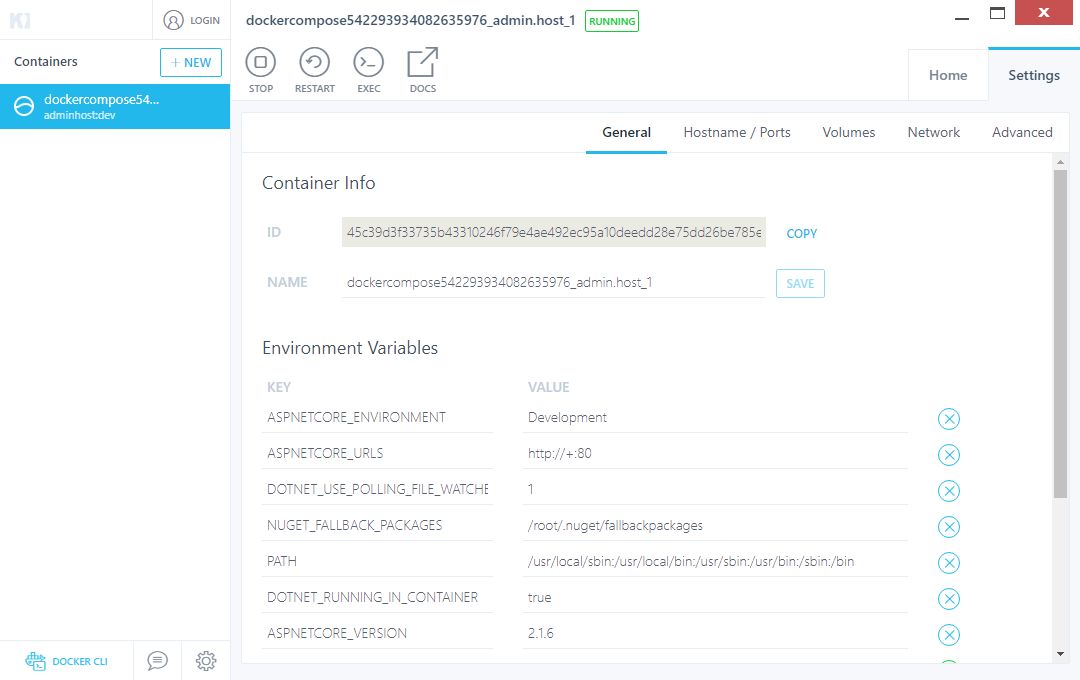
另外,Kitematic 集成了Docker Hub,允许通过搜索、拉取任何需要的镜像,并在上面部署应用。它同时也能很好地切换到命令行模式。目前,它包括了自动映射端口、可视化更改环境变量、配置卷、流式日志以及其它功能。
注意:如果安装完成后如果无法打开,请将Kitematic安装后的文件迁移到Docker指定目录【C:\Program Files\Docker\Kitematic】。
kitematic 是开源的,如果大家有兴趣,可以访问其开源库下载全部源代码进行研究:
https://github.com/docker/kitematic
往期内容
Docker最全教程——从理论到实战(一)
Docker最全教程——从理论到实战(二)
Docker最全教程——从理论到实战(三)
Docker最全教程——从理论到实战(四)
Docker最全教程——从理论到实战(五)
长按识别二维码,了解更多精彩内容



如果喜欢作者的文章,请关注“magiccodes”订阅号以便第一时间获得最新内容。本文版权归作者和湖南心莱信息科技有限公司共有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文连接,否则保留追究法律责任的权利。
QQ群:
编程交流群<85318032>
产品交流群<897857351>
![P4332-[SHOI2014]三叉神经树【LCT】](http://pic.xiahunao.cn/P4332-[SHOI2014]三叉神经树【LCT】)
![牛客题霸 [ 环形链表的约瑟夫问题] C++题解/答案](http://pic.xiahunao.cn/牛客题霸 [ 环形链表的约瑟夫问题] C++题解/答案)
)
)

![P7405-[JOI 2021 Final]雪玉【二分】](http://pic.xiahunao.cn/P7405-[JOI 2021 Final]雪玉【二分】)
![牛客题霸 [ 集合的所有子集] C++题解/答案](http://pic.xiahunao.cn/牛客题霸 [ 集合的所有子集] C++题解/答案)
I love max and multiply(转化))

)

![牛客题霸 [最长重复子串] C++题解/答案](http://pic.xiahunao.cn/牛客题霸 [最长重复子串] C++题解/答案)
)
)
![P6563-[SBCOI2020]一直在你身旁【dp,单调队列】](http://pic.xiahunao.cn/P6563-[SBCOI2020]一直在你身旁【dp,单调队列】)
![牛客题霸 [字符串的排列] C++题解/答案](http://pic.xiahunao.cn/牛客题霸 [字符串的排列] C++题解/答案)
)
)

![P5470-[NOI2019]序列【模拟费用流】](http://pic.xiahunao.cn/P5470-[NOI2019]序列【模拟费用流】)