虽然作业还没有做完，但是我还是放不下它，对此，我只想说：
今天你对作业爱理不理，明天它就让你补到飞起

练习上手：乘法逆元

题目

题解

对于这种求[1，n]区间的乘法逆元，
费马小定理?

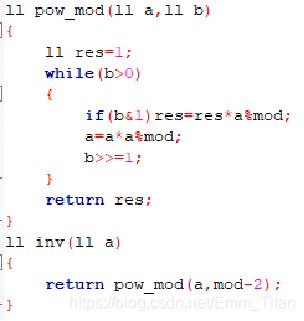
扩展欧几里得?

这两种对于求单个是比较有用的，O（nlogn）
但是对于这种区间求解就需要O（n）的线性筛了

for ( int i = 2;i <= n;i ++ )inv[i] = inv[p % i] * ( p - p / i ) % p;

至于为什么是这样子的，我们来进行简单推理：
首先应该要了解
对于数字A,B存在$A\ast X\equiv 1（modB$），则称X为A对B的逆元。
一般这个乘法逆元是运用在需要取模而过程中又涉及到除法运算的时候，
将其转化为乘法计算

进入证明?：

记$T=p/i,K=p$%$i$
则有$K+T\ast i=p$，被除数等于商乘除数加余数
即$K+T\ast i\equiv 0(mod$ $p)$
变形：$K\equiv -T\ast i(mod$ $p)$
两边同时除以$i\ast K$
–>$1/i\equiv -T/K(mod$ $p)$
$1/i$就是i的逆元，
因为这两个相乘取模p同余1，同时：除以K就相当于乘以K的逆元
接下来，将$T=p/i,K=p$%$i$带入进去?
$inv[i]=-p/i\ast inv[p$%$i]$(mod $p)$
为了防止出现负数，就加一个$p\ast inv[p$%$i]$，利用取模的运算律
$inv[i]=inv[p$%$i]\ast (p-p/i)$%$p$

代码实现

#include <cstdio>
#define LL long long
#define MAXN 3000005
int n, p;
LL inv[MAXN];
int main() {scanf ( "%d %d", &n, &p );inv[1] = 1;printf ( "1\n" );for ( int i = 2;i <= n;i ++ ) {inv[i] = inv[p % i] * ( p - p / i ) % p;printf ( "%lld\n", inv[i] );}return 0;
}

ok，让我们随着难度的增加慢慢深入，就先去养养?，体验农村生活

曹冲养猪?（互质的中国剩余定理）

题目

题解

这道题，还好还好，麻痹自己，模板也是可以自己，慢慢看懂的，我就不多证明了，
主要是我懒得打了。。。

取模定理：两数不能整除，若被除数扩大（或缩小）了几倍，而除数不变，则其商和余数也同时扩大（或缩小）相同的倍数（余数必小于除数）。
如果a%b=c，那么如果x%b=c * 2，此时有x=a * 2；
转化为求通解问题，即：
求解同余方程组
x≡ a1​(mod m1​)
x≡ a2​(mod m2​)
x≡ a3​(mod m3​)
…
x≡ ak​(mod mk​)​
其中m1,m2,m3…mk为两两互质的整数求x的最小非负整数解

M是输入的所有m[i]的乘积，Ti是M/mi的逆元


接下来就是模板套上去就可以了，在这里我只想补充，int128是个好玩意儿啊！！

代码实现

#include <cstdio>
#define MAXN 15
#define LL __int128
int n;
int m[MAXN], r[MAXN];void print ( LL x ) {if ( x > 9 )print ( x / 10 );putchar ( ( x % 10 ) + '0' );
}void exgcd ( LL a, LL b, int &x, int &y ) {if ( ! b ) {x = 1;y = 0;return;}exgcd ( b, a % b, y, x );y -= ( a / b ) * x;
} int main() {scanf ( "%d", &n );for ( int i = 1;i <= n;i ++ )scanf ( "%d %d", &m[i], &r[i] );LL lcm = 1, ans = 0;int x, y;for ( int i = 1;i <= n;i ++ )lcm = lcm * m[i];for ( int i = 1;i <= n;i ++ ) {LL tp = lcm / m[i];exgcd ( tp, m[i], x, y );x = ( x % m[i] + m[i] ) % m[i];ans = ( ans % lcm + tp * r[i] % lcm * x % lcm ) % lcm;}LL res = ( ans % lcm + lcm ) % lcm;print ( res );return 0;
} 

Strange Way to Express Integers（不互质的中国剩余定理）

题目

题解

那么，当模数不两两互质
即求：
解同余方程组
x≡ a1​(mod m1​)
x≡ a2​(mod m2​)
x≡ a3​(mod m3​）…
x≡ ak​(mod mk​)​
其中m1,m2,m3…mk是不一定两两互质的整数求x的最小非负整数解
我们先考虑：只有两个数该怎么处理
可以得到：
$x=a1+k1\ast m1$
$x=a2+k2\ast m2$
$k2\ast m2-k1\ast m1=a1-a2$
四不四很像 $ax+by=c$
设m1,m2的gcd为g，$a1-a2=c$
1）当c不是g的倍数时，exgcd无解
2)如果是，

则用exgcd求出$k2\ast m2+(-k1)\ast m1=gcd(m1,m2)$
因为c是g的倍数，两边同时乘以一个c/g，即k1乘上c/g得到
$k2\ast m2+(-k1)\ast m1=c解为-k1$

$X=a1-k1\ast m1$
这样就求出了x。
我们设这个x为x0
所以，可以得到的通解为$x=x0+k\ast lcm(m1,m2)$

将这个方程转化一下，可以得到一个新的同余方程
$x=x0(mod$ $lcm(m1,m2))$

我们便成功的将两个方程转化为了一个方程
后面以此类推，得到最后一个x0，即为我们所需要的答案。

上模板讲解?
M是上一次的最小公倍数lcm
R是上一次的x0，及我们的当前答案

R = a[1], M = m[1];
FOR(1~N)
gcd = exgcd ( M, m[i], x, y );
//k2*m2+(-k1)*m1=gcd(m1,m2)，这里M就是m1，m[i]就是m2，x，y是对应的k系数
c = R - a[i];
x = c / gcd * x % m[i];
//x此时就是k2*m2+(-k1)*m1=c中的-k1
R -= x * M;
//更新新的X答案m，X=a1-k1*m1(如果是➖，参照这个方程)，
//x=x0+k*lcm(m1,m2)（如果是➕，参照这个方程）
M = M / gcd * m[i];
//更新新的lcm
R %= M;

代码实现

#include <cstdio>
#define MAXN 100005
#define LL long long
int n;
int m[MAXN], a[MAXN];LL exgcd ( LL a, LL b, LL &x, LL &y ) {if ( ! b ) {x = 1;y = 0;return a;}LL d = exgcd ( b, a % b, y, x );y -= ( a / b ) * x;return d;
} LL gcd, R, M, x, y, c;int main() {while ( scanf ( "%d", &n ) != EOF ) {bool flag = 0;for ( int i = 1;i <= n;i ++ )scanf ( "%d %d", &m[i], &a[i] );R = a[1], M = m[1];for ( int i = 2;i <= n;i ++ ) {gcd = exgcd ( M, m[i], x, y );c = R - a[i];if ( c % gcd ) {flag = 1;printf ( "-1\n" );break;}x = c / gcd * x % ( m[i] / gcd );R -= x * M;M = M / gcd * m[i];R %= M;}if ( ! flag )printf ( "%lld\n", ( R % M + M ) % M );} return 0;
} 

好了，我已经被榨干了，去做其他的DP和数论了，ヾ(￣▽￣)Bye_Bye