P3258 [JLOI2014]松鼠的新家

题意：

n个点，n-1条边，给出每个点的拜访顺序，问每个点经过几次（最后一次移动不算拜访）

题解：

题意明确后就很好做了，对于给定的x和y，我们只需要分别将x和y到lca(x,y)经过的点加一即可
但是这样直接做肯定不行
有两个方法：

1. 树上差分
2. 树链剖分

树上差分

参考题解
我们先考虑对于数组，我们指定连续一段加一
我们现在对a2到a6区间进行加一
现在处理差分数组，我们对a2加一，对a7减一
差分属猪的定义:a[i] = a[i-1] + 差分数组[i]
也就是我们并没有改变区间的值，而是改变的两个数之间的相对大小

对于树上差分：
父亲节点u = 其所有的子节点 + 他本身的差分数组
我们现在改变S到T边上所有点的值
我们对S的父亲节点减1，对T加1

//把s->t路径上所有点均加w,
chafen[t] += w;
chafen[s的父节点] -= w; 

当计算每个点具体值时：

for(遍历与 u 相连的每一个子节点 v){num[u] += num[v]; 
}  
num[u] += chafen[u];//加上差分数组 

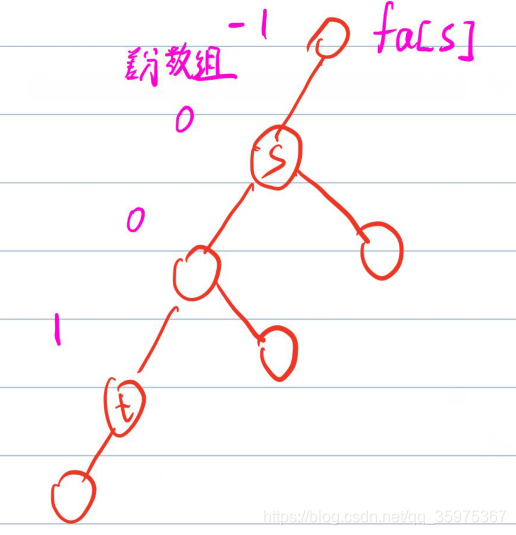
在本题中结合lca即可

代码：

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <cmath>
using namespace std;const int maxn = 300050;
const int maxm = maxn << 1;
int N, M;
int a[maxn], t1, t2;
int head[maxn], cnt;struct Edge{int u, v, next;
}edge[maxm];inline void addedge(int u, int v){edge[++cnt].u = u;edge[cnt].v = v;edge[cnt].next = head[u];head[u] = cnt;
}int fa[maxn][31], dep[maxn];void dfs(int u, int faa){fa[u][0] = faa, dep[u] = dep[faa] + 1;for(int i = 1; i <= 30; i++){fa[u][i] = fa[ fa[u][i - 1] ][i - 1];}for(int i = head[u]; i ; i = edge[i].next){int v = edge[i].v;if(v == faa)continue;dfs(v, u);}
} inline int lca(int x, int y){if(dep[x] < dep[y])swap(x,y);for(int i = 30; i >= 0; i--){if(dep[ fa[x][i] ] >= dep[y]) x = fa[x][i];}if(x == y)return x;for(int i = 30; i >= 0; i--){if(fa[x][i] != fa[y][i]){x = fa[x][i], y = fa[y][i];}}return fa[x][0];
}int num[maxn];int answer(int u, int faa){for(int i = head[u]; i ; i = edge[i].next){int v = edge[i].v;if(v == faa)continue;answer(v, u);num[u] += num[v];}
}
int main(){cin>>N;for(int i = 1; i <= N; i++){cin>> a[i];}for(int i = 1; i < N; i++){cin>> t1>> t2;addedge(t1, t2);addedge(t2, t1);}dfs(1, 0);for(int i = 1; i <= N - 1; i++){int u = a[i], v = a[i + 1];int t = lca(u, v);num[ fa[t][0] ]	-= 1;num[ t ] -= 1;num[ u ] += 1;num[ v ] += 1;}answer(1,0);for(int i = 2; i <= N; i++){num[a[i]]--;}for(int i = 1; i <= N; i++){cout<<num[i]<<endl;}
}

树链剖分

树链剖分就直接进行区间修改加一就行哈

代码：

这个代码我调了半个晚上，哭了哭了，终于调好了

#include<bits/stdc++.h>
typedef long long ll;
using namespace std;
inline int read(){int s=0,w=1;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();//s=(s<<3)+(s<<1)+(ch^48);return s*w;
}
const int maxn=1e6+9;
int a[maxn];
struct node{int u,v,next;
}edge[maxn];
int cnt=0;
int tot=0;
int n;
int head[maxn];
void add(int u,int v)
{edge[++cnt].v=v;edge[cnt].next=head[u];head[u]=cnt;
}
//---
int tr[maxn<<2],laz[maxn<<2];
inline void pushup(int rt)
{tr[rt]=tr[rt<<1]+tr[rt<<1|1];
}
inline void pushdown(int rt,int l,int r)
{int len=(r-l+1);laz[rt<<1]+=laz[rt];laz[rt<<1|1]+=laz[rt];tr[rt<<1]+=laz[rt]*(len-(len>>1));tr[rt<<1|1]+=laz[rt]*(len>>1);laz[rt]=0;
}
inline void build(int rt,int l,int r)
{if(l==r){tr[rt]=0;return ;}int mid=l+r>>1; build(rt<<1,l,mid);build(rt<<1|1,mid+1,r);pushup(rt); 
}
inline int query(int rt,int l,int r,int ip)
{if(l==ip&&r==ip)return tr[rt];if(laz[rt])pushdown(rt,l,r);int mid=l+r>>1;int ress=0;if(ip<=mid)ress+=query(rt<<1,l,mid,ip);if(ip>mid)ress+=query(rt<<1|1,mid+1,r,ip);return ress;
}
inline void update(int rt,int l,int r,int L,int R,int k)
{if(L<=l&&r<=R){int len=(r-l+1);laz[rt]+=k;tr[rt]+=k*len;}else {if(laz[rt])pushdown(rt,l,r);int mid=l+r>>1;if(L<=mid)update(rt<<1,l,mid,L,R,k);if(R>mid)update(rt<<1|1,mid+1,r,L,R,k);pushup(rt);}
}
//---
int fa[maxn],dep[maxn],siz[maxn],id[maxn],top[maxn],son[maxn];
inline int updrange(int x,int y,int k)
{while(top[x]!=top[y]){if(dep[top[x]]<dep[top[y]])swap(x,y);update(1,1,n,id[top[x]],id[x],k);x=fa[top[x]];}if(dep[x]>dep[y])swap(x,y);update(1,1,n,id[x],id[y],k);
}
inline void dfs1(int x,int f,int deep)
{dep[x]=deep;fa[x]=f;siz[x]=1;int maxson=-1;for(int i=head[x];i;i=edge[i].next){int v=edge[i].v;if(v==f)continue;dfs1(v,x,deep+1);siz[x]+=siz[v];if(siz[v]>maxson){son[x]=v;maxson=siz[v];}}
}
inline void dfs2(int x,int topf)
{id[x]=++tot;top[x]=topf;if(!son[x])return ;dfs2(son[x],topf);for(int i=head[x];i;i=edge[i].next){int v=edge[i].v;if(v==fa[x]||v==son[x])continue;dfs2(v,v);}
}
void print()
{for(int i=1;i<=n;i++){printf("%d\n",query(1,1,n,id[i]));//cout<<<<endl;}
//	printf("----\n");
}
int main()
{cin>>n;for(int i=1;i<=n;i++)cin>>a[i];for(int i=1;i<n;i++){int x,y;cin>>x>>y;add(x,y);add(y,x);}dfs1(a[n],0,1);dfs2(a[n],a[n]);build(1,1,n);updrange(a[1],a[1],1);//print();for(int i=1;i<n;i++){updrange(a[i],a[i+1],1);updrange(a[i],a[i],-1);//	print();}updrange(a[n],a[n],-1);print();return 0;
}