DP专练博客

T1：最大子矩阵

题目

这里有一个n*m的矩阵，请你选出其中k个子矩阵，使得这个k个子矩阵分值之和最大。注意：选出的k个子矩阵不能相互重叠。

输入格式
第一行为n,m,k（1≤n≤100,1≤m≤2,1≤k≤10），接下来n行描述矩阵每行中的每个元素的分值(每个元素的分值的绝对值不超过32767)。
输出格式
只有一行为k个子矩阵分值之和最大为多少。

输入输出样例
输入
3 2 2
1 -3
2 3
-2 3
输出
9

题解

首先看到这个小的数据范围（尤其是m），就不明所以然地心动。。。

我们先来考虑m=1的情况
这个问题就转化为了求一个区间的k个互不重复的线段的和的最大值
肯定都会做$DP[i][j]$：表示到i位置为止一共已经选了j个区间的合法最大值
状态转移方程如下：
$DP[i][j]=max(DP[last][j-1]+val[i],DP[last][j])(0\le last<i)$

---

那么受m=1的影响启发，虽然矩阵变成了二维，也不会变得过于复杂
设$DP[i][j][k]$：表示第一列已经枚举到了i位，第二列已经枚举到了j位，一共选了k个矩阵
但是可以发现当$i==j$的时候这个状态可以由i和j同时以宽度为2进行转移，所以会多一个转移方程式
综上，转移方程式如下：
$$DP[i][j][k]=\{\begin{array}{r}max(DP[lasti][j][k-1]+val[i][j],DP[i][lastj][k-1]+a[i][j])\\ val就是从last到i为止这个宽度为2的子矩阵值的和:\\ DP[i][j][k]=max(DP[last][last][k-1]+val)(i==j)\\ 别忘了还可以不选这个点:\\ DP[i][j][k]=max(DP[last][j][k],DP[i][last][k])\end{array}$$

---

最后分享如何计算这个子矩阵的值
我们可以定义一个二维数组sum[i][3]第二维表示是第几列，i表示本列到第i位时的值
这样val就变得很好算了

代码实现

#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
int n, m, k;
int matrix[105][3], sum[105][3];
int dp[105][105][15];
int main() {scanf ( "%d %d %d", &n, &m, &k );memset ( dp, -0x7f, sizeof ( dp ) );for ( int i = 1;i <= n;i ++ )for ( int j = 1;j <= m;j ++ ) {scanf ( "%d", &matrix[i][j] );sum[i][j] = sum[i - 1][j] + matrix[i][j];}for ( int i = 0;i <= n;i ++ )for ( int j = 0;j <= m;j ++ )dp[i][j][0] = 0;for ( int p = 1;p <= k;p ++ )for ( int i = 1;i <= n;i ++ )for ( int j = 1;j <= n;j ++ ) {dp[i][j][p] = max ( dp[i - 1][j][p], dp[i][j - 1][p] );for ( int last = 0;last < i;last ++ )dp[i][j][p] = max ( dp[i][j][p], dp[last][j][p - 1] + sum[i][1] - sum[last][1] );for ( int last = 0;last < j;last ++ )dp[i][j][p] = max ( dp[i][j][p], dp[i][last][p - 1] + sum[j][2] - sum[last][2] );if ( i == j )for ( int last = 0;last < i;last ++ )dp[i][j][p] = max ( dp[i][j][p], dp[last][last][p - 1] + sum[i][1] - sum[last][1] + sum[j][2] - sum[last][2] );}	printf ( "%d", dp[n][n][k] );	return 0;
} 

没有放表情包真是让人怪不舒服的，ヾ(•ω•`)o

T2：守卫

题目

九条可怜是一个热爱运动的女孩子

这一天她去爬山，她的父亲为了她的安全，雇了一些保镖，让他们固定地呆在在山的某些位置，来实时监视九条可怜，从而保护她。

具体来说，一座山可以描述为一条折线，折线的下方是岩石。这条折线有 n 个折点，每个折点上有一个亭子，第 ii 个折点的坐标是(i,hi) 。九条可怜只可能会在亭子处玩耍，那些保镖也只会在亭子处监视可怜。

由于技术方面的原因，一个保镖只能监视所有他能看得到的，横坐标不超过他所在位置的亭子。我们称一个保镖能看到一个亭子 p ，当且仅当他所在的亭子 q 和 p 的连线不经过任何一块岩石。特别地，如果这条连线恰好经过了除了 p,q 以外的亭子，那么我们认为保镖看不到可怜。

雇佣保镖是一件很费钱的事情，可怜的父亲希望保镖越少越好。

可怜的父亲还希望得到详尽的雇佣保镖的方案，他知道有些亭子可能正在维修，他想对所有的 1≤l≤r≤n 计算：如果事先已知了只有区间 [l,r] 的亭子可以用来玩耍(和监视)，那么最少需要多少个保镖，才能让[l,r] 中的每一个亭子都被监视到。

可怜的父亲已经得到了一个结果，他希望和你核实他的结果是否正确。

输入格式
第一行输入一个整数n表示亭子的数目。 接下来一行n个整数，第 i 个整数 hi表示第i个亭子的坐标是(i,hi)
输出格式
对所有的1≤l≤r≤n 计算：如果事先已知了可怜只会在 [l,r] 这个区间的亭子里面玩耍，那么最少需要多少个保镖，才能让 [l,r] 中的每一个亭子都被监视到。由于输出量太大，可怜的父亲只要你输出所有[l,r]中的每一个亭子都被监视到。由于输出量太大，可怜的父亲只要你输出所有[l,r]的答案的异或即可。

输入输出样例
输入
3
2 3 1
输出
3
说明/提示
样例解释
如果r−l+1≤2 ,那么答案显然是1 。 如果l=1,r=n ,那么答案是 2 ,需要安排两个保镖在 (2,3),(3,1) 两个位置监视可怜。

数据范围与提示
对于 30% 的数据，n≤20 。
对于 70% 的数据，n≤500 。
对于 100% 的数据，n≤5000，1≤hi≤10⁹

题解

首先通过题意我们知道对于$[l,r]$而言，守卫只能安排在这个区间且只能往前看，他的脖子不允许他转180
那么r这个点就必须安排一个守卫

---

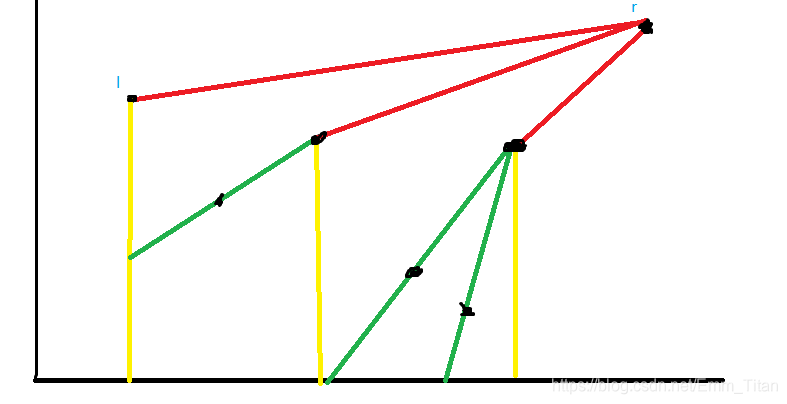
观察这个图，假设现在守卫在r，那么他能看见的亭子必须夹角得逐步变大
也就是说他的视线在不断往上移，是无法往下看的，这个可以利用两点确定一条直线的K值进行判断
我们可以$O(n^2)$预处理出i，j两个点之间是否可以彼此看见

紧接着不难想到，r看不见的区间是彼此相互独立的，即
r可以监视的一个点x，那么[x+1,r)的点都不能监视比x更靠前的点
感性理解：x太高了，挡住了后面点的视线，使得他们看不见x前面的点
举个栗子理解：就是在第二个绿色板块里面的点无法看见第一个绿色板块里面的点，
因为第二根黄线的那个点太高了，遮住了第二个绿色板块点的视线

---

设$DP[l][r]$表示在$[l,r]$区间中最少要设多少个守卫

知道了当我们固定右端点，那么这个点不能监视到的一些区间$[li,ri]$是相互独立的，
所以想要监视$[li,ri]$就必须在$ri$或者$ri+1$处设置保镖，
于是DP转移方程式
$$dp[l][r]=1+\sum min(dp[li][ri],dp[li][ri+1])$$

这样做是O(n³)的，但是发现对于每一个$[li,ri]$区间只与紧邻的后一个看不见的区间的有瓜葛
我们就可以考虑枚举右端点，这样就可以在往前面扫的过程中维护那个$\sum$，从而复杂度降到了O(n²)

代码实现

#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
#define MAXN 5005
int n, result;
int h[MAXN];
int dp[MAXN][MAXN];
bool look[MAXN][MAXN];
int main() {scanf ( "%d", &n );for ( int i = 1;i <= n;i ++ )scanf ( "%d", &h[i] );for ( int i = 1;i <= n;i ++ ) {double k = 1e9;for ( int j = i - 1;j;j -- )if ( ( h[i] - h[j] ) * 1.0 / ( i - j ) < k ) {k = ( h[i] - h[j] ) * 1.0 / ( i - j );look[j][i] = 1;}}dp[1][1] = dp[2][2] = dp[1][2] = 1;for ( int i = 3;i <= n;i ++ ) {int sum = 0, last = i;dp[i][i] = 1;for ( int j = i - 1;j;j -- ) {if ( look[j][i] ) {if ( ! look[j + 1][i] )sum += min ( dp[j + 1][last], dp[j + 1][last - 1] );dp[j][i] = sum + 1;last = j;}elsedp[j][i] = min ( dp[j][last - 1], dp[j][last] ) + sum + 1;}}for ( int i = 1;i <= n;i ++ )for ( int j = 1;j <= i;j ++ )result ^= dp[j][i];printf ( "%d", result );return 0;
}

T3：手机号码

题目

人们选择手机号码时都希望号码好记、吉利。比如号码中含有几位相邻的相同数字、不含谐音不吉利的数字等。手机运营商在发行新号码时也会考虑这些因素，从号段中选取含有某些特征的号码单独出售。为了便于前期规划，运营商希望开发一个工具来自动统计号段中满足特征的号码数量。

工具需要检测的号码特征有两个：号码中要出现至少 3 个相邻的相同数字；号码中不能同时出现 8 和 4。号码必须同时包含两个特征才满足条件。满足条件的号码例如：13000988721、23333333333、14444101000。而不满足条件的号码例如：1015400080、10010012022。

手机号码一定是 11 位数，前不含前导的 0。工具接收两个数 L 和 R，自动统计出 [L,R]区间内所有满足条件的号码数量。L 和 R 也是 11 位的手机号码。

输入格式
输入文件内容只有一行，为空格分隔的 2 个正整数 L,R
输出格式
输出文件内容只有一行，为 1 个整数，表示满足条件的手机号数量。

输入输出样例
输入
12121284000 12121285550
输出
5
说明/提示
样例解释：满足条件的号码： 12121285000、 12121285111、 12121285222、 12121285333、 12121285550。

数据范围：10¹⁰≤L≤R<10¹¹

题解

首先我们可以将$[l,r]$运用差分思想转化成$[1,r]-[1,l-1]$，这肯定大家都想得到

---

对于这种位数固定的，且比较小的题目，就可以思考数位DP

设$DP[p][last][last$_$last][flag][limit][flag$_$4][flag$_$8]$表示：
模拟到电话号码的p位时，p+1位的值为last，p+2位的值为last_last

flag表示到当前状态为止，是否已经出现了至少3 个相邻的相同数字
flag=1：已经出现；flag=0：还未出现

limit表示到当前状态为止，前面是否都取的是最大值
limit=1：抵着最大值取的；limit=0：不是抵着最大值取的
eg：12345678910，当p指向3时，limit=1，则表示p+1位取的是2，p+2位取的是1
都是取的当前位能取的最大值

flag_4表示到当前状态为止，是否出现过数字4
flag_4=1：已经出现；flag_4=0仍未出现

flag_8表示到当前状态为止，是否出现过数字8
flag_8=1：已经出现；flag_8=0仍未出现

---

这里要注意几个点：
1.flag_4和flag_8不能同时为1，在搜索时要特判处理
2.我们由于要把电话号码值x拆分成各个数位，我们储存i位的值的num数组是倒着的
所以搜索时就从大到小，这也是为什么上面的例子p+1的电话数位反而在p前面
3.如果搜索到p时，limit是1，那么这个数位的值就被限制了$[0,num[p]]$
否则，这个数位就可以取$[0,9]$
4.可采取记忆化搜索进行剪枝

---

转移方程式：
p肯定是p-1，p的上一个就变成了p-1的上上一个，p就变成了p-1的上一个

flag如果先前是1，就不改变，如果在p时刚好p与p+1与p+2相等，就可以变成1，
往下传，所以这里我们要用$||$

limit如果是1，那么这个位置如果也取的最大值，就往下传；但如果不是，后面的数位还是可以取$[0,9]$，所以这里要用$\&\&$

flag_4如果之前出现过，就传下去；如果当前位是4，就可以赋值成1，所以用$||$
flag_8亦是如此

其实很简单的，只要会数位DP，可是我不会啊，这就很尴尬了

代码实现

#include <cstdio>
#include <cstring>
#define LL long long
LL dp[15][15][15][2][2][2][2];
int num[15];LL dfs ( int p, int last, int last_last, bool flag, bool limit, bool flag_4, bool flag_8 ) {if ( flag_4 && flag_8 )return 0;if ( p == 0 )//搜索到末尾了return flag;//flag=1即出现过至少三个是连续的相同数字，这一个电话号码就是合理的if ( dp[p][last][last_last][flag][limit][flag_4][flag_8] != -1 )return dp[p][last][last_last][flag][limit][flag_4][flag_8];int Limit = limit ? num[p] : 9;LL ans = 0;for ( int i = 0;i <= Limit;i ++ )ans += dfs ( p - 1, i, last, flag || ( i == last && i == last_last ), limit && ( i == Limit ), flag_4 || ( i == 4 ), flag_8 || ( i == 8 ) );return dp[p][last][last_last][flag][limit][flag_4][flag_8] = ans;
}LL solve ( LL x ) {if ( x < 1e10 )//特判，如果位数不够电话号码的11位return 0;LL result = 0;memset ( dp, -1, sizeof ( dp ) );int len = 0;while ( x ) {num[++ len] = x % 10;x /= 10;}for ( int i = 1;i <= num[len];i ++ )//不能出现前导零result += dfs ( 10, i, 0, 0, ! ( i < num[len] ), i == 4, i == 8 );return result;
}int main() {LL l, r;scanf ( "%lld %lld", &l, &r );printf ( "%lld", solve ( r ) - solve ( l - 1 ) );return 0;
}