真的太难了，刚开始是直接用模板不断A题，其实自己根本不是很理解，于是今天放弃了刷题时间，理解并背诵了这个模板，写了这篇blog

二叉查找树BST(Binary Search Tree)定义

二叉查找树(Binary Search Tree)是基于插入思想的一种在线的排序数据结构，它又叫二叉搜索树(Binary Search Tree)、二叉排序树(Binary Sort Tree)，简称BST

这种数据结构的基本思想是在二叉树的基础上，规定一定的顺序，使数据可以有序地存储

二叉查找树运用了像二分查找一样的查找方式，并且基于链式结构存储，从而实现了高效的查找效率和完美的插入时间

---

二叉查找树(Binary Search Tree)或者是一棵空树，或者是具有下列性质的二叉
树：

1. 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
2. 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
3. 它的左、右子树也分别为二叉查找树

我只是为了让大家理解下面Treap的定义罢了

Treap定义

Treap是一种平衡树。这个单词的构造选取了Tree(树)的前两个字符和Heap(堆)的后三个字符，
Treap = Tree + Heap。
顾名思义，Treap把BST和Heap结合了起来。
它和BST一样满足许多优美的性质，而引入堆目的就是为了维护平衡。

---

Treap在BST的基础上，添加了一个修正值。在满足BST性质的基础上，Treap节点的修正值还满足最小堆性质 。最小堆性质可以被描述为每个子树根节点都小于等于其子节点。

---

Treap的定义
Treap可以定义为有以下性质的二叉树：

1. 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值，而且它
   的根节点的修正值小于等于左子树根节点的修正值；
2. 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值，而且它
   的根节点的修正值小于等于右子树根节点的修正值；
3. 它的左、右子树也分别为Treap。

修正值是节点在插入到Treap中时随机生成的一个值，它与节点的值无关。

---

Treap维护平衡的原理
我们发现，BST会遇到不平衡的原因是因为有序的数据会使查找的路径退化成链，
而随机的数据使BST退化的概率是非常小的

在Treap中，修正值的引入恰恰是使树的结构不仅仅取决于节点的值，还取决于修正值的值然而修正值的值是随机生成的，出现有序的随机序列是小概率事件，所以Treap的结构是趋向于随机平衡的

---

模板合集（均为$O(logn)$）

先给明要用到的数组含义：
Size：表示节点数量也可作最后一个点编号
cnt[p]：表示编号为p，值为x在treap中插入的次数
key[p]：表示该点p的值为x
rd[p]：就是我们自己搞的修正值，用rand函数随机生成
siz[p]：编号为p的子树包括本身在内的节点数量即大小
son[p][2]：son[p][0]表示p的左儿子，son[p][1]表示p的右儿子

---

push_up模板

就是更新x的子树大小，一定要多次更新，因为后面的操作总是要用到
一句话：不用白不用，能多用就多用

void push_up ( int x ) {siz[x] = siz[son[x][0]] + siz[son[x][1]] + cnt[x];
}

---

旋转模板

为了使Treap中的节点同时满足BST性质和小根堆性质，不可避免地要对其结构进行调整，调整方式被称为旋转(Rotate)
在维护Treap的过程中，只有两种旋转 ，分别是左旋和右旋。旋转是相对于子树而言的，左旋和右旋的命名体现了旋转的一条性质1：
左旋一个子树，会把它的根节点旋转到根的左子树位置，同时根节点的右子节点成为子树的根；
右旋一个子树，会把它的根节点旋转到根的右子树位置，同时根节点的左子节点成为子树的根

如图：

性质2：旋转后的子树仍然满足BST性质

---

void rotate ( int &x, int d ) {//0左旋，1右旋 int p = son[x][!d];son[x][!d] = son[p][d];son[p][d] = x;push_up ( x );push_up ( p );x = p;
}

---

插入模板

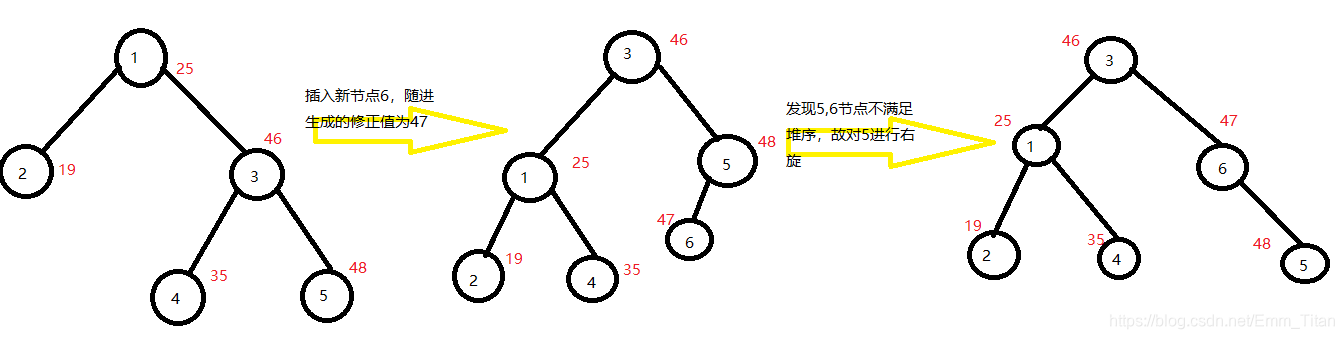
在Treap中插入元素，与在BST中插入方法相似。首先找到合适的插入位置，然后建立新的节点，存储元素。但是要注意建立新的节点的过程中，会随机地生成一个修正值，这个值可能会破坏堆序，因此我们要根据需要进行恰当的旋转。具体方法如下：

1. 从根节点开始插入；
2. 如果要插入的值小于等于当前节点的值，在当前节点的左子树中插入，插入后
   如果左子节点的修正值小于当前节点的修正值，对当前节点进行右旋；
3. 如果要插入的值大于当前节点的值，在当前节点的右子树中插入，插入后如果
   右子节点的修正值小于当前节点的修正值，对当前节点进行左旋；
4. 如果当前节点为空节点，在此建立新的节点，该节点的值为要插入的值，左右
   子树为空，插入成功
   

void insert ( int &rt, int x ) {if ( ! rt ) {rt = ++ Size;siz[rt] = cnt[rt] = 1;key[rt] = x;rd[rt] = rand();return;}if ( key[rt] == x ) {cnt[rt] ++;siz[rt] ++;return;}int d = x > key[rt];insert ( son[rt][d], x );if ( rd[rt] < rd[son[rt][d]] )//说明是新插入的点，往另外一边旋转 rotate ( rt, !d );push_up ( rt );
/*如果旋转了就白做了，因为旋转中就已经更新了，
但是如果没旋转，这个就有用了，因为插入了以前的size就是错的*/
}

---

删除模板

Treap的删除因为要维护堆序，比较好的方法是利用旋转的方法把要删除的结点旋转到叶结点位置，再做删除操作。

情况一，该节点为叶节点，则该节点是可以直接删除的节点。若该节点有非空子节点，用非空子节点代替该节点的，否则用空节点代替该节点，然后删除该节点。

情况二，该节点有两个非空子节点。我们的策略是通过旋转，使该节点变为可以直接删除的节点。如果该节点的左子节点的修正值小于右子节点的修正值，右旋该节点，使该节点降为右子树的根节点，然后访问右子树的根节点，继续讨论；反之，左旋该节点，使该节点降为左子树的根节点，然后访问左子树的根节点，继续讨论，直到变成可以直接删除的节点

---

例如：要删除节点6，找到节点6，发现6有两个儿子，但是右儿子的修正值小于左儿子，选择左旋

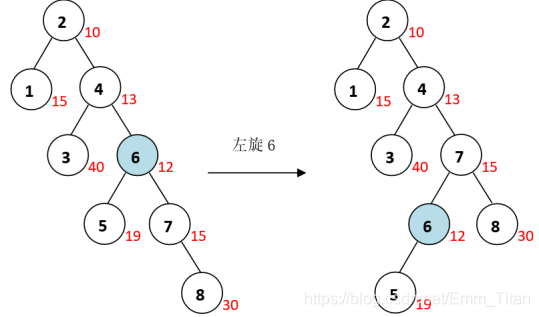
接着发现6只剩下一个儿子了，就直接右旋让左儿子代替它的位置随后删掉

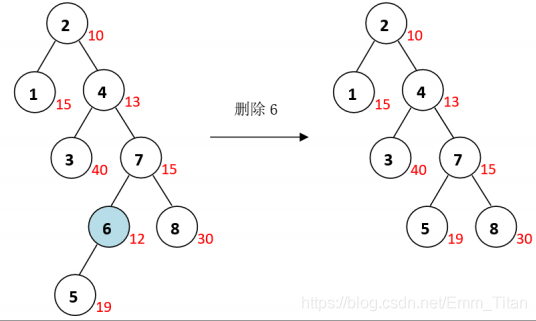
void delet ( int &rt, int x ) {if ( ! rt )return;if ( x != key[rt] )delet ( son[rt][x > key[rt]], x );else {if ( ! son[rt][0] && ! son[rt][1] ) {cnt[rt] --;siz[rt] --;if ( ! cnt[rt] )rt = 0;}else if ( son[rt][0] && ! son[rt][1] ) {rotate ( rt, 1 );delet ( son[rt][1], x );}else if ( ! son[rt][0] && son[rt][1] ) {rotate ( rt, 0 );delet ( son[rt][0], x );}else {int d = rd[son[rt][0]] > rd[son[rt][1]];rotate ( rt, d );delet ( son[rt][d], x );}}push_up ( rt );
}

---

接下来就比较轻松了，好理解了

查找前驱模板

找前驱我们发现，其实就是一直往左儿子找，如果节点p与查找值x大小比较后要查找p的右儿子，这个右儿子就是x的一个前驱但不一定是最接近的，所以需要比较并继续往下找，掘地三尺

int pre ( int rt, int x ) {if ( ! rt )return -INF;if ( key[rt] >= x )return pre ( son[rt][0], x );elsereturn max ( key[rt], pre ( son[rt][1], x ) );
}

---

查找后驱模板

找后驱我们发现与前驱相似，其实就是一直往右儿子找，如果节点p与查找值x大小比较后要查找p的左儿子，这个左儿子就是x的一个前驱但不一定是最接近的，所以需要比较

int suf ( int rt, int x ) {if ( ! rt )return INF;if ( key[rt] <= x )return suf ( son[rt][1], x );elsereturn min ( key[rt], suf ( son[rt][0], x ) );
}

---

查找键值key模板

就是与siz子树个数比较，看属于哪个部分

int find ( int rt, int x ) {if ( ! rt )return 0;if ( siz[son[rt][0]] >= x )return find ( son[rt][0], x );else if ( siz[son[rt][0]] + cnt[rt] < x )return find ( son[rt][1], x - cnt[rt] - siz[son[rt][0]] );elsereturn key[rt];
}

---

查找节点的修正值rank模板

和find差不多的思想，应该很好理解的

int search_rank ( int rt, int x ) {if ( ! rt )return 0;if ( key[rt] == x )return siz[son[rt][0]] + 1;if ( key[rt] < x )return siz[son[rt][0]] + cnt[rt] + search_rank ( son[rt][1], x );return search_rank ( son[rt][0], x );
}

PS：rd的比较问题

认真的同学会发现，我在写讲解博客的时候是维护的rd从小到大，而代码却是写的从大到小，其实这rd本来就是我们自己强加的修正值，所以本质是没有太大的区别的，只需要注意对应insert和delet维护好自己锁定的rd顺序就行了

1：

insert：if ( rd[p] < rd[son[p][d]] )
delet：int d = rd[son[p][0]] > rd[son[p][1]];

2：

insert：if ( rd[p] > rd[son[p][d]] )
delet：int d = rd[son[p][0]] < rd[son[p][1]];

---

例题：普通平衡树

题目

点击查看题目

代码实现

既然是入门模板题，自然是把所有的模板拼接上再加上输入输出即可AC，不再多说！！

#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;
#define MAXN 100005
#define INF 0x7f7f7f7f
int n, Size;
int siz[MAXN], cnt[MAXN], key[MAXN], rd[MAXN];
int son[MAXN][2];void push_up ( int x ) {siz[x] = siz[son[x][0]] + siz[son[x][1]] + cnt[x];
}void rotate ( int &x, int d ) {int p = son[x][!d];son[x][!d] = son[p][d];son[p][d] = x;push_up ( x );push_up ( p );x = p;
}void insert ( int &rt, int x ) {if ( ! rt ) {rt = ++ Size;siz[rt] = cnt[rt] = 1;key[rt] = x;rd[rt] = rand();return;}if ( key[rt] == x ) {cnt[rt] ++;siz[rt] ++;return;}int d = x > key[rt];insert ( son[rt][d], x );if ( rd[rt] < rd[son[rt][d]] )rotate ( rt, !d );push_up ( rt );
}void delet ( int &rt, int x ) {if ( ! rt )return;if ( x != key[rt] )delet ( son[rt][x > key[rt]], x );else {if ( ! son[rt][0] && ! son[rt][1] ) {cnt[rt] --;siz[rt] --;if ( ! cnt[rt] )rt = 0;}else if ( son[rt][0] && ! son[rt][1] ) {rotate ( rt, 1 );delet ( son[rt][1], x );}else if ( ! son[rt][0] && son[rt][1] ) {rotate ( rt, 0 );delet ( son[rt][0], x );}else {int d = rd[son[rt][0]] > rd[son[rt][1]];rotate ( rt, d );delet ( son[rt][d], x );}}push_up ( rt );
}int search_rank ( int rt, int x ) {if ( ! rt )return 0;if ( key[rt] == x )return siz[son[rt][0]] + 1;if ( key[rt] < x )return siz[son[rt][0]] + cnt[rt] + search_rank ( son[rt][1], x );return search_rank ( son[rt][0], x );
}int find ( int rt, int x ) {if ( ! rt )return 0;if ( siz[son[rt][0]] >= x )return find ( son[rt][0], x );else if ( siz[son[rt][0]] + cnt[rt] < x )return find ( son[rt][1], x - cnt[rt] - siz[son[rt][0]] );elsereturn key[rt];
}int pre ( int rt, int x ) {if ( ! rt )return -INF;if ( key[rt] >= x )return pre ( son[rt][0], x );elsereturn max ( key[rt], pre ( son[rt][1], x ) );
}int suf ( int rt, int x ) {if ( ! rt )return INF;if ( key[rt] <= x )return suf ( son[rt][1], x );elsereturn min ( key[rt], suf ( son[rt][0], x ) );
}int main() {scanf ( "%d", &n );int root = 0;while ( n -- ) {int opt, x;scanf ( "%d %d", &opt, &x );switch ( opt ) {case 1 : insert ( root, x );break;case 2 : delet ( root, x );break;case 3 : printf ( "%d\n", search_rank ( root, x ) );break;case 4 : printf ( "%d\n", find ( root, x ) );break;case 5 : printf ( "%d\n", pre ( root, x ) );break;case 6 : printf ( "%d\n", suf ( root, x ) );break;}}return 0;
} 

如果有任何问题欢迎提出，bye，让我们与非旋treap不见不散