Rolling The Polygon Gym - 102222B

题意：

给你一个多边形，给你内部一个点Q，多边形在平面上滚动一周（当有一个边第二次触地滚动停止），问Q的轨迹长度

题解：

计算几何题目
自己一直不是很擅长也不是很想做，嫌麻烦，但是考了n次自己也不会n次，所以决定跳出舒适圈，开始攻克计算几何
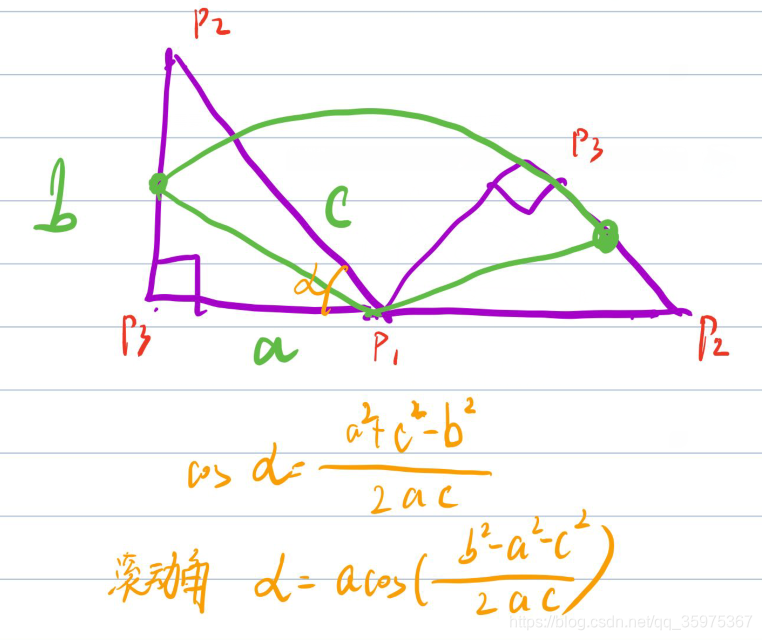
我们注意多边形和目标点滚动的方式和轨迹，Q点每次移动轨迹都是一段弧，要求弧长就要知道半径和移动角度。
如图一次滚动，我们可以看出滚动角的顶点是p1，滚动角是p1，p2和p1，p3形成的夹角α，旋转角度就是180°-滚动角
因为都是一个图形内，所以其他边旋转角度是多少，Q就是多少。
现在知道Q的旋转角度，半径更好求就是Q到p1的距离
因为每个顶点都会是滚动角的顶点，所以求出Q到各顶点的距离，以及各个角
详细看代码

代码：

#include<bits/stdc++.h>
#define pii pair<int,int>
typedef long long ll;
using namespace std;
inline int read(){int s=0,w=1;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();//s=(s<<3)+(s<<1)+(ch^48);return s*w;
}
const double PI=acos(-1.0);
double dis(pii x,pii y){return sqrt((x.first-y.first)*(x.first-y.first)+(x.second-y.second)*(x.second-y.second));
}
double angle(double r,pii x,pii y, pii z){double a=dis(y,z),b=dis(x,z),c=dis(x,y);double radian=acos(1.0*(a*a+c*c-b*b)/(2*a*c));return r*(PI-radian);
}
int main()
{int t,n,x,y;cin>>t;int cas=0;while(t--){int n;cin>>n;vector<pii >v(n);for(int i=0;i<n;i++){cin>>x>>y;v[i]={x,y};}double ans=0.0;cin>>x>>y;for(int i=0;i<n;i++){double r=dis({x,y},v[i]);ans+=angle(r,v[(i-1+n)%n],v[i],v[(i+1+n)%n]);}printf("Case #%d: %.3f\n",++cas,ans);}return 0;
}