description

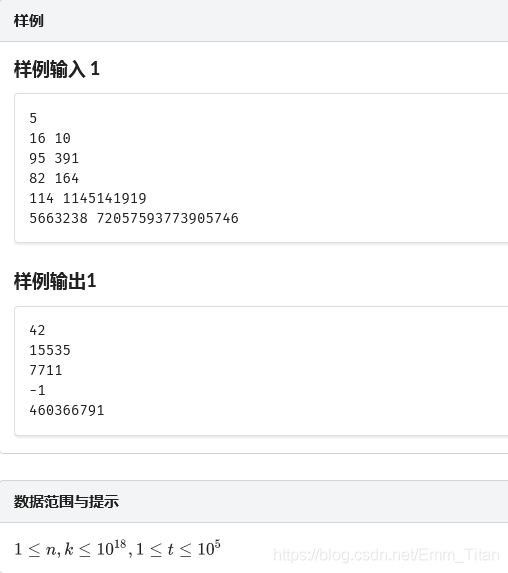
solution

打表yyds
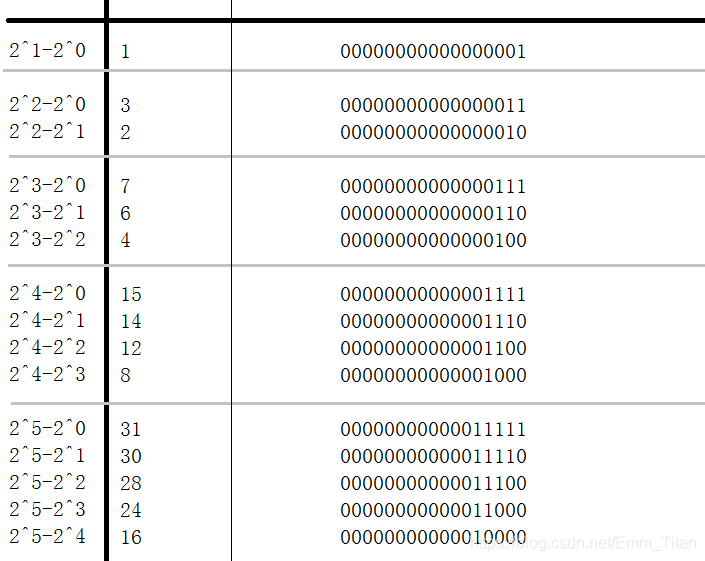其实符合条件的个数跟$n$（非题目中的意思）有着等差数列公式的千丝万缕关系
所以可以二分出具体值
最后答案的取值范围一定是长成$[,)$，左闭右开的形式的
而且两个边界一定是只差了最小的那个$1$，那么答案的二进制长相也是固定的

同样二分出$1$的具体位置即可
这里与组合数挂钩，可以预处理部分小的组合数降低查询时间复杂度

私以为还是有思维难度的！

code

#include <iostream>
#include <cstdio>
#include <cmath>
using namespace std;
#define MAX 1e18
#define ll long long
#define mod 998244353
ll c[3005][3005];ll qkpow1( ll x, ll y ) {ll ans = 1;while( y ) {if( y & 1 ) ans = ans * x % mod;x = x * x % mod;y >>= 1;}return ans;
}ll qkpow2( ll x, ll y ) {ll ans = 1;while( y ) {if( y & 1 ) ans *= x;x *= x;y >>= 1;}return ans;
}ll calc( ll n ) {return n * ( n + 1 ) >> 1;
}ll C( ll n, ll m ) {if( n <= 3000 && m <= 3000 ) return c[n][m];if( m > n - m ) m = n - m;if( n >= 1e7 && m >= 3 ) return MAX + 1;__int128 d1 = 1, d2 = 1;for( int i = 1;i <= m;i ++ ) d1 *= i;for( int i = n - m + 1;i <= n;i ++ ) {d2 *= i;if( d2 > d1 * MAX ) return MAX + 1;}return d2 / d1;
}void solve( ll n, ll k, ll ans ) {ll t = 0, tmp;while( k > ( tmp = C( n, t ) ) ) k -= tmp, t ++;int last = n;for( ll i = 1;i <= t;i ++ ) {ll l = 1, r = last, pos;while( l <= r ) {ll mid = ( l + r ) >> 1;if( C( mid - 1, t - i + 1 ) < k ) pos = mid, l = mid + 1;else r = mid - 1;}last = pos - 1;k -= C( pos - 1, t - i + 1 );ans = ( ans + qkpow1( 2, pos - 1 ) ) % mod;}printf( "%lld\n", ans );
}void init( int n = 3000 ) {for( int i = 0;i <= n;i ++ )for( int j = 1;j <= i;j ++ )c[i][j] = MAX + 1;for( int i = 0;i <= n;i ++ ) {c[i][0] = 1;for( int j = 1;j <= i;j ++ )c[i][j] = min( c[i][j], c[i - 1][j] + c[i - 1][j - 1] );}
}int main() {init();int T; ll n, k;scanf( "%d", &T );while( T -- ) {scanf( "%lld %lld", &n, &k );ll t = sqrt( n << 1 );while( calc( t ) > n ) t --;ll t1 = n - calc( t ), t2 = t - t1;if( ! t1 ) {if( k == 1 ) printf( "%lld\n", ( qkpow1( 2, t ) - 1 + mod ) % mod );else printf( "-1\n" );}else if( t2 < 60 && qkpow2( 2, t2 ) < k )printf( "-1\n" );else solve( t2, k, ( qkpow1( 2, t1 ) - 1 + mod ) % mod * qkpow1( 2, t2 + 1 ) % mod );}return 0;
}