题目链接

题解：

比赛时就直接写了一个暴力sort交上，能骗一点分是一点
昨晚看了acwing的讲解，现在结合我的思路更新正解
题目中设计两个操作，一个是选定前x个数，使其降序，另一个是选定后y个数，使其升序
问最后操作完，输出序列
题目就两个操作，我们考虑多种情况：
1.连续出现多个操作一。图中蓝色区域为操作1，如果连续出现多个操作1，虽然区间有长有短，但效果都是将区间内降序，我们不难发现最后有效果的是最长的区间部分（即图中第三个蓝区间），因为这个操作排完序后，之后连续的操作1都不会其效果（因为已经排好序）
说的有些啰嗦，总结：连续操作1取最长区间

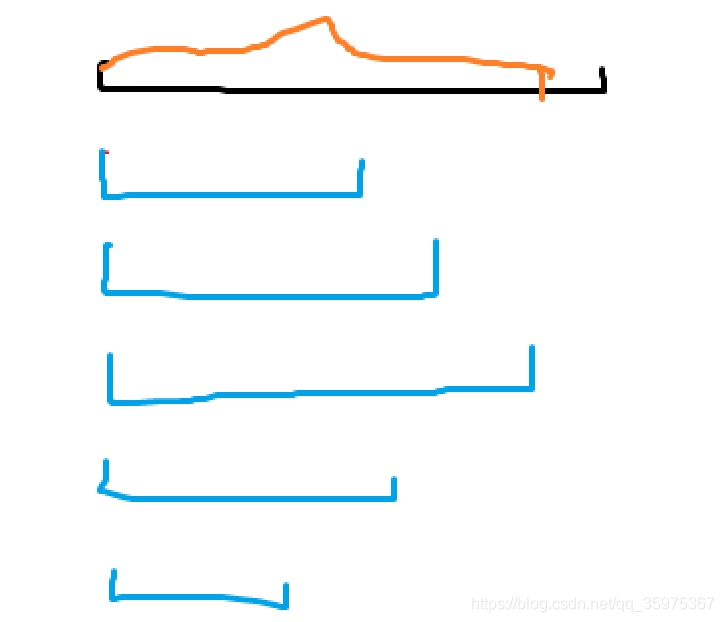
2.连续的操作2
同理：连续的操作2，我们也取最长部分
情况1和情况2使得最终的操作是1和2更替进行，（因为如果有连续就取最长）

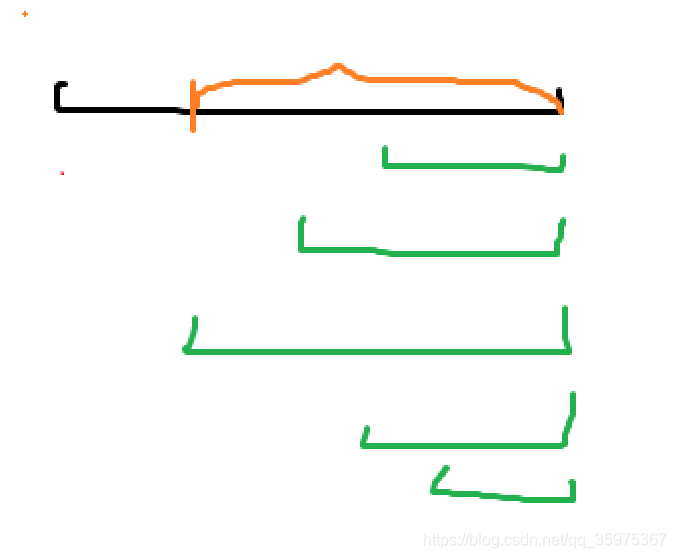
3.操作1与操作2交替
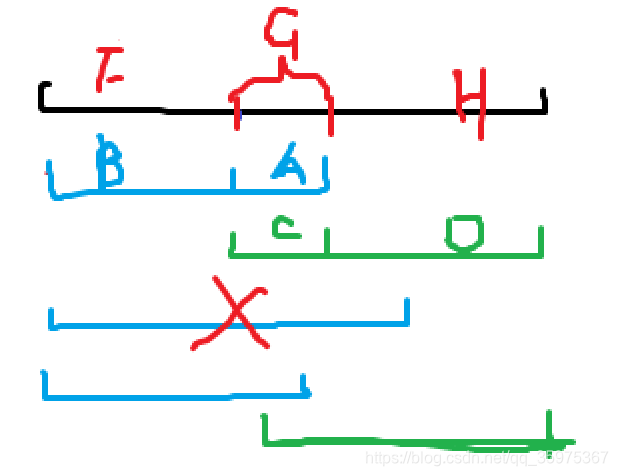
图中蓝色部分为操作1，绿色部分为操作2，
首先我们要知道序列一开始是升序的（即黑色区间），所以F中的数<G<H
第一个操作肯定是操作1，因为操作2没影响
操作1为降序，B>A，而绿区间为升序，我们要注意H区间的数是大于F和G的，我们操作1只对区间A，B进行了修改，所以H>A和B，那么操作2对C和D区间（即G和H）进行修改时，D区间保持不变，（因为D区间本来就是升序，为啥要变）但是C区间目前是降序，所以要变成升序。
这样看来，改变的只有
接下来应该是操作1了，如果接下来的操作1比之前的操作1的区间长度长，那之前的操作1的区间就可以省略，因为后来的操作完全将之前的覆盖了，如果把之前的操作1省略掉，就会出现两个操作2相邻，为了保证两个操作交替进行，所以上一个操作1和操作2都会消失（看下面第二个图中被矩形选中的部分为省略）
因为我们可以得到，操作1和2交替进行，且相比于上一次操作，本次操作的区间长度越来越短，因此相交部分也越来越短，直到两者不再相交，到这时修改将不再起作用，每次操作其实反转的也只有相交部分

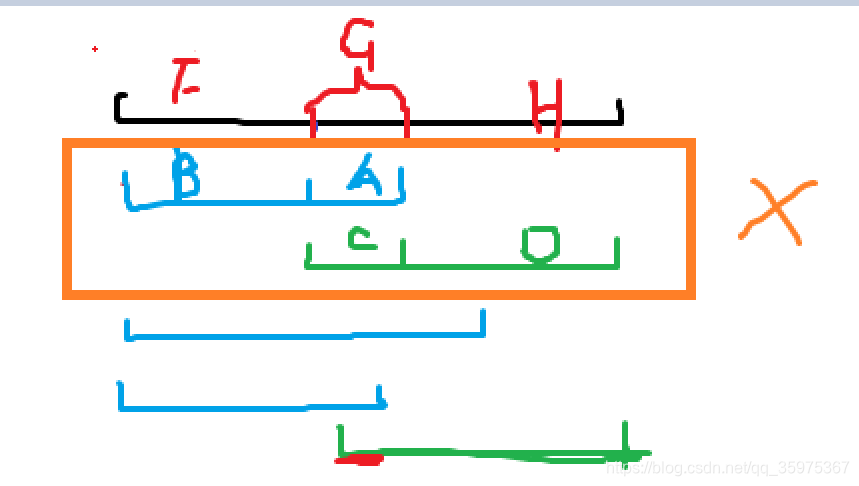
我们用这个图来总结一下：红色线段部分修改，蓝色线段保持上一次状态
我们设红色线段的两端分别是x和y，因为我们每次要做的就是反转区间[x,y]，且x和y是不断向内靠近的
反转的操作可以用平衡树或者线段树，但是没必要
因为我们说了相交区间越来越小，当执行操作1时，本质是y向内靠，当执行操作2时，本质是x向内靠，
当x和y向内靠时，经过的点在后续不会发生改变，那我们就直接给他赋值即可，我们用一个变量K，K一开始为n，第一个操纵为1，我们要将y移动到第一个红线的右端（下图），移动过程中给非红线的部分一次赋值，并k–

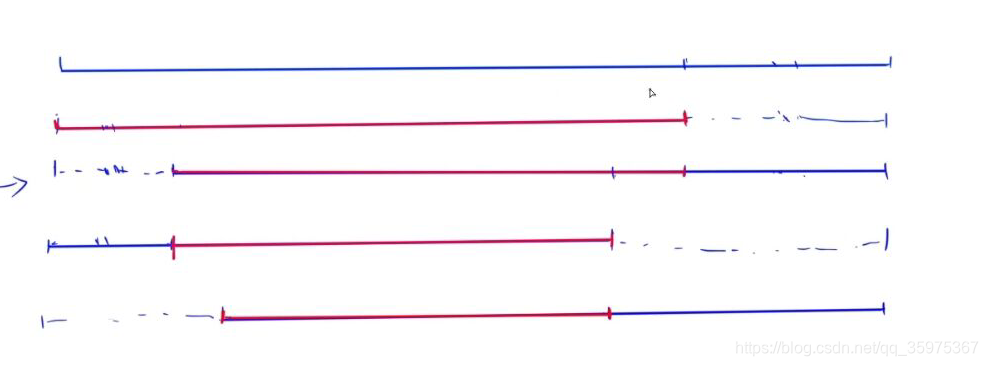
最终实现的效果如下:

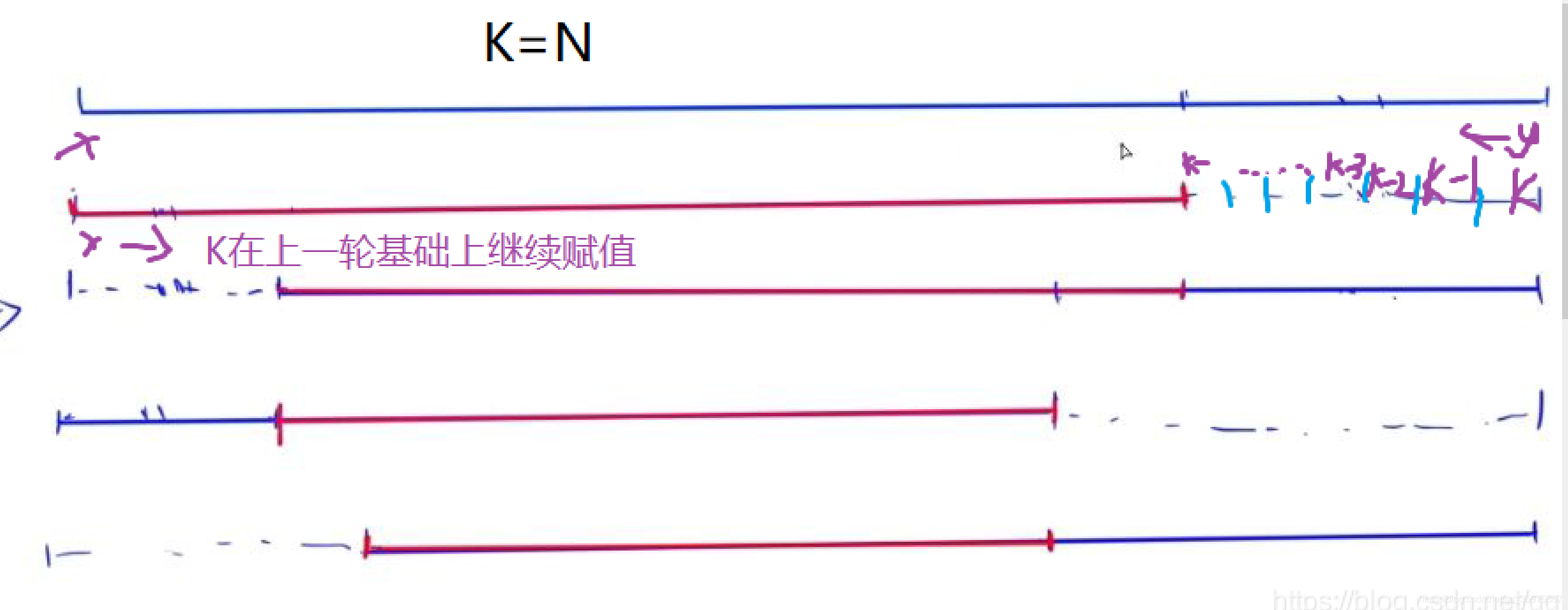
这就实现了反转的操作
我讲的不是很清楚，有什么问题可以评论区里问

代码：

好题，代码为yxc写的，这个代码逻辑比我写的清晰
代码我有详细注释

#include <iostream>
#include <cstring>
#include <algorithm>#define x first
#define y secondusing namespace std;typedef pair<int, int> PII;const int N = 100010;int n, m;
PII stk[N];
int ans[N];int main()
{scanf("%d%d", &n, &m);int top = 0;while (m -- ){int p, q;scanf("%d%d", &p, &q);if (!p)//操作1 {while (top && stk[top].x == 0) q = max(q, stk[top -- ].y);//出现连续的操作1，我们取最大 while (top >= 2 && stk[top - 1].y <= q) //如果当前的操作1比上一次的操作1范围大，则将上一次操作1和操作2删除 top -= 2;stk[ ++ top] = {0, q};//存本次最佳操作 }else if (top)//操作2 &&且操作1已经进行过（操作二第一个用没效果） {while (top && stk[top].x == 1) q = min(q, stk[top -- ].y);while (top >= 2 && stk[top - 1].y >= q) top -= 2;stk[ ++ top] = {1, q};}}int k = n, l = 1, r = n;for (int i = 1; i <= top; i ++ ){if (stk[i].x == 0)//如果是操作1 while (r > stk[i].y && l <= r) ans[r -- ] = k -- ;//移动r值 ，并赋值 elsewhile (l < stk[i].y && l <= r) ans[l ++ ] = k -- ; if (l > r) break;}if (top % 2)while (l <= r) ans[l ++ ] = k -- ;elsewhile (l <= r) ans[r -- ] = k -- ;for (int i = 1; i <= n; i ++ )printf("%d ", ans[i]);return 0;
}