所谓半平面交，就是和“半平先生”当面交谈。顾名思义，这是一个源于日本的算法。

（逃）

前言

感觉应用很灵活的一个算法，一切有两个变量的线性规划问题都可以转化为半平面交。
有时可能要注意取等问题（指射箭），但多数时候似乎并不用。

解析

半平面的表示

首先，我们需要一个简洁的方式表达半平面。
不禁想到，我们可以利用叉积的符号来判断点是在一条线的顺时针还是逆时针方向。那么类似的，我们可以用一个点x和一个方向向量d表示一个半平面，一个点p属于这个半平面，当且仅当 $\overrightarrow{d}\times \overrightarrow{XP}>0$（也就是点在方向向量的左侧），是否取等取决于半平面本身的开闭。

inline bool in(const line &l,const V o){return (l.d^(o-l.a))>eps;}
inline bool out(const line &l,const V o){return (l.d^(o-l.a))<-eps;}

流程

有了一个合适的表示方法后，我们就可以开始尝试解决半平面交问题了，顾名思义，这个问题就是：

给出若干个半平面，求它们的交。

（显然，得到的一定是一个凸包。）
怎么做呢？
首先，我们把所有点半平面按照极角排序，极角可以利用 atan2(y,x) 函数很方便的求出。
当两个向量共线时，显然只有靠左的那个是有用的，我们让有用的放在前面。（这样在后面的算法中遇到没用的时候可以直接跳过，避免求平行线的交点而出现错误）

bool cmp(const line l1,const line l2){double t1=atan2(l1.d.y,l1.d.x),t2=atan2(l2.d.y,l2.d.x);if(abs(t1-t2)>eps) return t1<t2;return in(l2,l1.a);
}

考虑维护一个双端队列来维护当前对答案有用的半平面，并记录每个半平面和前一个半平面的交点。
维护分为如下步骤：

1. 每加入一个半平面时， 若队尾与队尾前一个的交点在当前半平面外，则不断弹出队尾。
2. 类似的，若队首和后一个的交点在当前半平面外，也不断弹出队首。
3. 加入当前半平面，并计算其与上一个半平面的交点。
4. 插入所有半平面后，若队尾与上一个的交点在队首半平面外，那么队尾也是无用的，弹出队尾所有没有用的半平面。
5. 最后，插入队尾与队首的交点，得到的封闭的凸包就是答案。

void half_plane(){sort(l+1,l+1+tot,cmp);st=1,ed=0;for(int i=1;i<=tot;i++){if(st<=ed&&abs(q[ed].d^l[i].d)<eps) continue;//和上一个共线，必然是无用向量 while(ed-st+1>=2&&out(l[i],pt[ed])) --ed;//先弹队尾 while(ed-st+1>=2&&out(l[i],pt[st+1])) ++st;q[++ed]=l[i];if(ed-st+1>=2) pt[ed]=jiaodian(q[ed-1],q[ed]);}while(ed-st+1>=2&&out(q[st],pt[ed])) --ed;//弹出队尾无用向量 if(ed-st+1>=2) pt[ed+1]=jiaodian(q[st],q[ed]),++ed;//加入队尾与队首的交点 m=ed-st;for(int i=1;i<=m;i++) a[i]=pt[st+i];a[m+1]=a[1];return;
}

细节

1. 可不可以先弹队首再弹队尾？

不可以！
考虑这两种写法不一样的情况，就是当我判断在半平面外的那个交点恰好就是队首和队尾的交点时。
也就是：

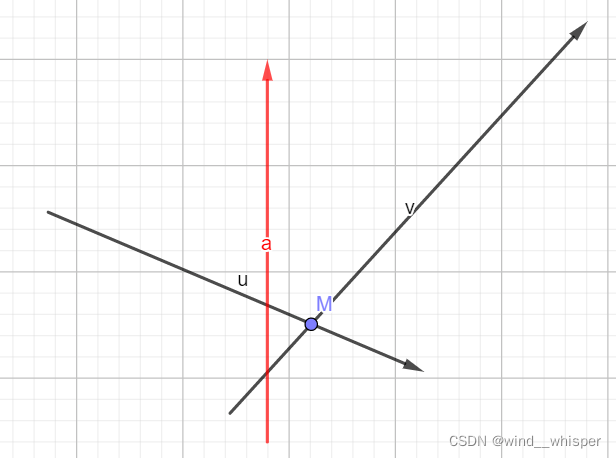
（图片来自：OI-wiki 半平面交）

显然这个时候弹队首会出错。

2. 如何判断交集为空或无边界？

考虑在正无穷远处加入四条与坐标轴平行的边，把整个平面框成一个大矩形，在进行半平面交算法。
这样就不会出现无边界情况，要判断也可以通过凸包内是否出现了那四条边来进行。
而且，这样之后，凸包元素不足三个就变成了答案无解的充要条件。
非常优美简洁。

代码

P4196 [CQOI2006]凸多边形 /【模板】半平面交

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define ull unsigned long long
#define debug(...) fprintf(stderr,__VA_ARGS__)
inline ll read(){ll x(0),f(1);char c=getchar();while(!isdigit(c)){if(c=='-')f=-1;c=getchar();}while(isdigit(c)){x=(x<<1)+(x<<3)+c-'0';c=getchar();}return x*f;
}//basic declare
//#define double long double
const double eps=1e-10;
const double pi=acos(-1.0);//---about vectors (or points)//definition
struct V{double x,y;V():x(0),y(0){}V(double a,double b):x(a),y(b){}
};
inline void input(V &a){scanf("%lf%lf",&a.x,&a.y);}
void print(const V &a,int op=1){printf("%g %g",a.x,a.y);putchar(op?10:32);}
//op:endl or space//basic operation
inline V operator + (const V &a,const V &b){return (V){a.x+b.x,a.y+b.y};}
inline V operator - (const V &a,const V &b){return (V){a.x-b.x,a.y-b.y};}
inline V operator * (const double &x,const V &a){return (V){a.x*x,a.y*x};}
inline V operator * (const V &a,const double &x){return (V){a.x*x,a.y*x};}
inline V operator / (const V &a,const double x){return (V){a.x/x,a.y/x};}
inline bool operator == (const V &a,const V &b){return abs(a.x-b.x)<eps&&abs(a.y-b.y)<eps;}
inline bool operator != (const V &a,const V &b){return !(a==b);}
inline double operator * (const V &a,const V &b){return a.x*b.x+a.y*b.y;}
inline double operator ^ (const V &a,const V &b){return a.x*b.y-a.y*b.x;}
inline double len(const V &a){return sqrt(a.x*a.x+a.y*a.y);}
inline V mid(const V &a,const V &b){return (V){(a.x+b.x)/2,(a.y+b.y)/2};}
inline V chui(const V &a){return (V){a.y,-a.x};}//not take direction into account
inline V danwei(const V &a){return a/len(a);}
inline double ang(const V &a,const V &b){return acos((a*b)/len(a)/len(b));}
inline V rotate(const V &o,double t){//COUNTER_CLOCKWISEdouble s=sin(t),c=cos(t);return (V){o.x*c-o.y*s,o.x*s+o.y*c};
}
struct line{V d,a;
};
void print(const line &l,int op=1){printf("point: ");print(l.a,0);printf("dir: ");print(l.d,op);
}
inline line trans(const V &a,const V &b){return (line){b-a,a};
}
inline line trans(const double &a,const double &b,const double &c,const double &d){
//given one point and directionreturn (line){(V){c,d},(V){a,b}};
}
inline V jiaodian(const line &u,const line &v){if(u.d==v.d){print(u);print(v);exit(0);}double k=((v.a-u.a)^v.d)/(u.d^v.d);return u.a+k*u.d;
}inline bool in(const line &l,const V o){return (l.d^(o-l.a))>0;}
inline bool out(const line &l,const V o){return (l.d^(o-l.a))<-eps;}const int N=1005;
int n,m;int tot,st,ed;
V a[N],pt[N];
line l[N],q[N];bool cmp(const line l1,const line l2){double t1=atan2(l1.d.y,l1.d.x),t2=atan2(l2.d.y,l2.d.x);if(abs(t1-t2)>eps) return t1<t2;return in(l2,l1.a);
}const double inf=1e9;
void half_plane(){l[++tot]=trans(0,0,1,0);//插入边界l[++tot]=trans(X,0,0,1);l[++tot]=trans(0,Y,-1,0);l[++tot]=trans(0,0,0,-1);sort(l+1,l+1+tot,cmp);st=1,ed=0;for(int i=1;i<=tot;i++){if(st<=ed&&abs(q[ed].d^l[i].d)<eps) continue;//和上一个共线，必然是无用向量 while(ed-st+1>=2&&out(l[i],pt[ed])) --ed;//先弹队尾 while(ed-st+1>=2&&out(l[i],pt[st+1])) ++st;q[++ed]=l[i];if(ed-st+1>=2) pt[ed]=jiaodian(q[ed-1],q[ed]);}while(ed-st+1>=2&&out(q[st],pt[ed])) --ed;//弹出队尾无用向量 if(ed-st+1>=2) pt[ed+1]=jiaodian(q[st],q[ed]),++ed;//加入队尾与队首的交点 m=ed-st;for(int i=1;i<=m;i++) a[i]=pt[st+i];a[m+1]=a[1];return;
}
signed main(){
#ifndef ONLINE_JUDGEfreopen("a.in","r",stdin);freopen("a.out","w",stdout);
#endifn=read();for(int i=1;i<=n;i++){m=read();for(int j=1;j<=m;j++) input(a[j]);a[m+1]=a[1];for(int j=1;j<=m;j++) l[++tot]=trans(a[j],a[j+1]);}half_plane();if(m<3){printf("0.000");return 0;}double res(0);for(int i=1;i<=m;i++) res+=(a[i]^a[i+1])/2;if(res<0) res=-res;printf("%.3lf\n",res);return 0;
}
/*
4
2 8
4 2
6 5
-8 2
*/