Acwing 1089. 烽火传递

题意：

有n个数，要保证每m个数中必须选一个，问所选数的最小总和是多少

题解：

我一开始设的状态为:dp[i]表示前i个数选完的最小值，第i个数可以选也可以不选，但是这样一个状态，如果要这么考虑的话应该开二维数组来表示状态，且答案不好求，所以我们改变状态定义：

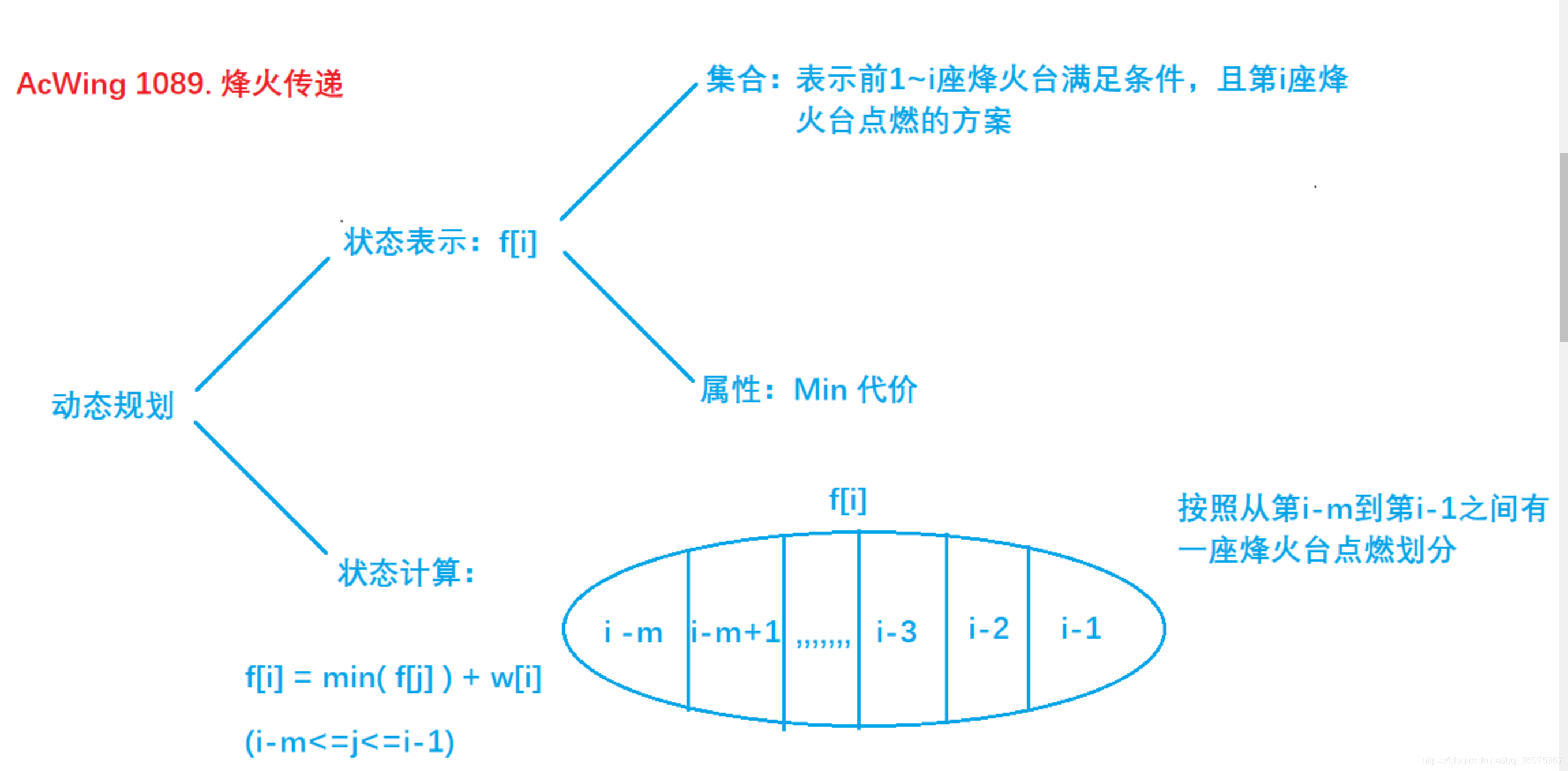
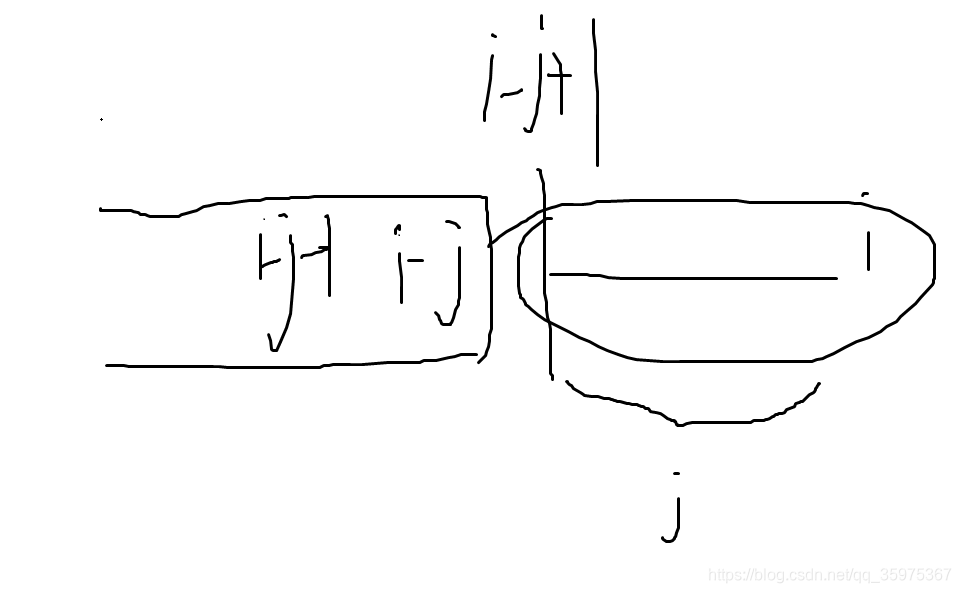
我们定dp[i]表示第i个必选的，且前i-1个满足条件的最小值
我们可以得到状态方程为：dp[i]=min(dp[x])+a[i],x∈[i-m,i-1]
dp[x]通过单调队列可以得到

那最终的答案是什么？想想我们的状态为dp[i]，前i-1个满足条件,第i个一定选择，那么也就是如果i∈[n-m+1,n],所有的情况就都会考虑到（即任意m个数都存在一个被选），所以答案就是min(dp[n-m+1],d[n-m+2]…dp[n])，在最后m个数中选一个的最小值情况

代码：

#include<bits/stdc++.h>
#define debug(a,b) printf("%s = %d\n",a,b);
typedef long long ll;
using namespace std;inline int read(){int s=0,w=1;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();//s=(s<<3)+(s<<1)+(ch^48);return s*w;
}
const int maxn=2e5+9;
int a[maxn];
int q[maxn];
int dp[maxn]; 
int main()
{int n,m;cin>>n>>m;for(int i=1;i<=n;i++){cin>>a[i];}int hh=0,tt=0;for(int i=1;i<=n;i++){if(q[hh]+m<i)hh++;dp[i]=dp[q[hh]]+a[i];while(hh<=tt&&dp[q[tt]]>=dp[i])tt--;q[++tt]=i;} int res=1e9;for(int i=n-m+1;i<=n;i++)res=min(res,dp[i]); cout<<res;return 0;
}
/*
dp[i]选择完前i个烽火台的最低花费
第i个可以选，也可以不选
dp[i]=dp[i-1]
如果选：
选择长度为j
dp[i]=min(dp[i-j])+a[i]
j:1~m
x:i-m ~ i-1
dp[i]=min(dp[x])+a[i]
*/