本文是关于 Newbe.Claptrap 项目主体内容的介绍，读者可以通过这篇文章，大体了解项目内容。

轮子源于需求

随着互联网应用的蓬勃发展，相关的技术理论和实现手段也在被不断创造出来。诸如 “云原生架构”、“微服务架构”、“DevOps” 等一系列关键词越来越多的出现在工程师的视野之中。总结来看，这些新理论和新技术的出现，都是为了解决互联网应用中出现的一些技术痛点：

更高的容量扩展性要求。在商业成功的基础前提下，互联网应用的用户数量、系统压力和硬件设备数量等方面都会随着时间的推移出现明显的增长。这就对应用本省的容量可扩展性提出了要求。这种容量可扩展性通常被描述为 “应用需要支持水平扩展”。

更高的系统稳定性要求。应用程序能够不间断运行，确保商业活动的持续进展，这是任何与这个应用系统相关的人员都希望见到的。但是要做到这点，通常来说是十分困难的。而现今的互联网应用在面对诸多同类竞争者的情况下，如果在这方面做得不够健全，那么很可能会失去一部分用户的青睐。

更高的功能扩展性要求。“拥抱变化”，当人们提到 “敏捷项目管理” 相关的内容时，都会涉及到的一个词语。这个词语充分体现了当今的互联网应用若要成功，在功能性上做到出彩做到成功是多么的重要。也从一个侧面体现了当前互联网环境下产品需求的多变。而作为系统工程师，在应用建立之初就应该考虑这点。

更高的开发易用度要求。这里所属的开发易用度是指，在应用系统自身在进行开发时的难易程度。要做到越易于开发，在应用自身的代码结构，可测试性，可部署性上都需要作出相应的努力。

更高的性能要求。这里提到的性能要求，是特指在系统容量增加时的性能要求。避免系统的单点性能问题，让应用系统具备可水平扩展的特性。通常来说，在性能出现问题时，若可以通过增加物理设备来解决问题，通常来说是最为简单的办法。而在不同的系统容量之下，系统性能的优化方案通常是不同的。因此结合应用场景进行技术方案的选型一直都是系统工程师所需要考虑的问题。

本项目，就是基于以上这些系统功能特性要求所总结出来的一套开发框架。这其中包含了相关的理论基石、开发类库和技术规约。

世界上本也不存在 “银弹”。一套框架解决不了所有问题。 ——不愿意透露姓名的月落

从需求出发

在讲解分布式系统时，常常会用到 “账号转账” 这个简单的业务场景来配合描述。这里阐述一下这个业务场景。

假设我们需要建设一个具备账号体系的业务系统。每个账号都有余额。现在需要执行一次转账操作，将账号 A 的余额中的 300 划转给账号 B。另外，基于上节的基本要求，我们在实现这个场景时，需要考虑以下这些内容：

需要应对系统容量的激增。应用初期可能只有 1000 个初始用户。由于应用推广效果良好以及机器人账号的涌入，用户数量实现了在一个月内实现了三个数量级的攀升，也就是增长到了百万级别。
需要考虑系统的稳定性和可恢复性。尽可能减少系统整体的平均故障时间，即使出现系统故障也应该是尽可能易于恢复的。也就是，要避免出现单点故障。
需要考虑业务的可扩展性。后续可能需要增加一些业务逻辑：按照账户等级限制日转账额、转账成功后进行短信通知、转账支持一定额度的免密转账、特定的账号实现 “T+1” 到账。
需要考虑代码的可测试性。系统的业务代码和系统代码能够良好的分离，能够通过单元测试的手段初步验证业务代码和系统代码的正确性和性能。

轮子的理论

本节将介绍一些和本框架紧密结合的理论内容，便于读者在后续的过程中理解本框架的工作过程。

Actor 模式

Actor 模式是一种并发编程模型。通过这种编程模型的应用可以很好的解决一些系统的并发问题。这里所提到的并发问题是指计算机对同一数据进行逻辑处理时，可能由于存在多个同时发起的请求可能导致数据出现不正确的问题。这个问题在进行多线程编程时一定会遇到的问题。举个简单的例子，假如在不加同步锁的情况下，使用 100 个线程并发对内存中的一个int变量执行++操作。那么最终这个变量的结果往往小于 100。此处 Actor 模式是如何避免此问题的。

首先，为了便于理解，读者在此处可以将 Actor 认为是一个对象。在面向对象的语言（Java、C# 等）当中，可以认为 Actor 就是通过new关键词创建出来的对象。不过这个对象有一些特别的特性：

拥有属于自身的状态。对象都可以拥有自身的属性，这是面向对象语言基本都具备的功能。在 Actor 模式中，这些属性都被统称为Actor的状态（State）。Actor 的状态由 Actor 自身进行维护。

这就强调了两点：

第一、Actor 的状态只能由自身进行改变，若要从外部改变 Actor 的状态，只能通过调用 Actor 才能改变。

640?wx_fmt=gif

第二、Actor 的状态只在 Actor 内部进行维护，不与当前 Actor 之外的任何对象共享。这里说的不共享也是强调其不能通过外部某个属性的改变而导致 Actor 内部状态的变化。这点主要是为了区别于一些具备 “对象引用” 语言特性的编程语言而言的。例如：在 C# 的class的public属性，假如是引用类型，那么在外部获得这个class之后是可以改变class中的属性的。但是这在 Actor 模式当中是不被允许的。

640?wx_fmt=gif

不过从 Actor 内部读取数据到外部，这仍然是允许的。

640?wx_fmt=gif

单线程。Actor 通常同一时间只能接受一个调用。这里所述的线程不完全是指计算机中的线程，是为了凸显 “Actor 同一时间只能处理一个请求的特性” 而使用的词语。假如当前 Actor 正在接受一个调用，那么剩余的调用都会阻塞，直到调用结束，下一个请求才允许被进入。这其实类似于一个同步锁的机制。通过这种机制就避免了对 Actor 内部状态进行修改时，存在并发问题的可能。具体一点说明：如果使用 100 个线程对一个 Actor 进行并发调用，让 Actor 对状态中的一个int变量进行++操作。最终这个状态的数值一定是 100。

640?wx_fmt=gif

不过单线程也不是绝对的，在不存在并发问题的请求情况下，允许并发处理。例如读取 Actor 中的状态，这通常不会有并发问题，那么此时就允许进行并发操作。

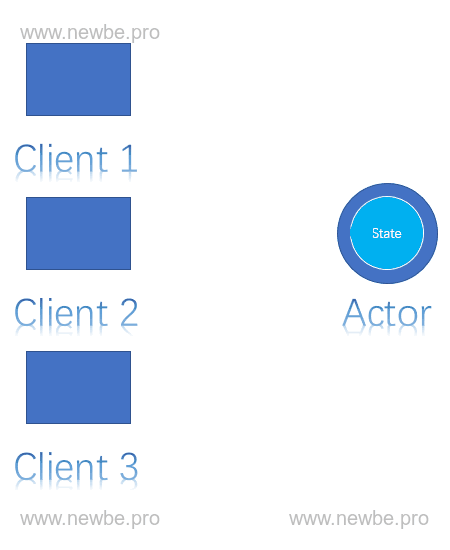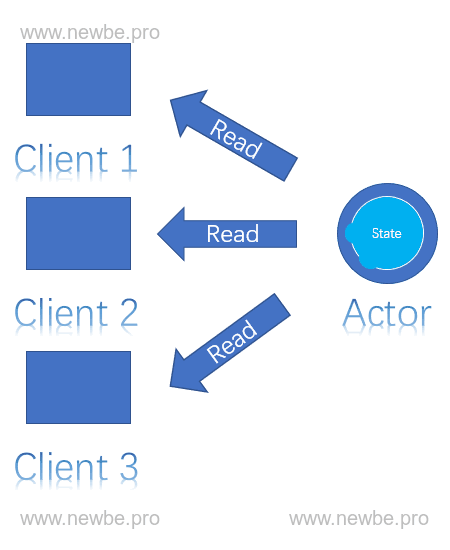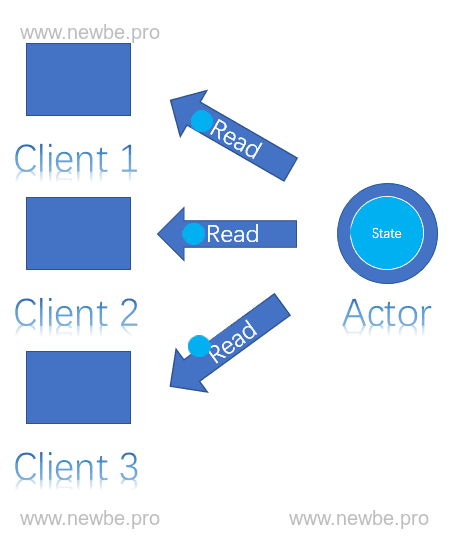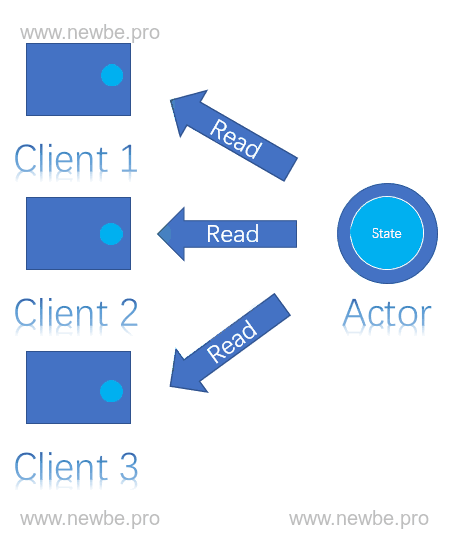
640?wx_fmt=gif

读到 Actor 单线程特性时，通常读者会考虑到这是否会导致 Actor 本身处理过慢而产生性能问题呢？关于这点，希望读者继续持有这个问题往后阅读，寻找答案。

事件溯源模式

事件溯源模式是一种软件设计思路。这种设计思路通常与传统的采用增删查改（CRUD）为主的系统设计思路相区别。CRUD 应用通常存在一些局限性：

通常来说 CRUD 应用会采用直接操作数据存储的做法。这样的实现方式可能会由于对数据库优化不足而导致性能瓶颈，并且这种做法会较难实现应用伸缩。
在特定的领域通常存在一些数据需要注意对并发问题进行处理，以防止数据更新的错误。这通常需要引入 “锁”、“事务” 等相关的技术来避免此类问题。但这样又有可能引发性能上的损失。
除非增加额外的审计手段，否则通常来说数据的变更历史是不可追踪的。因为数据存储中通常保存的是数据最终的状态。

与 CRUD 做法对比，事件溯源则从设计上避免了上述描述的局限性。接下来围绕上文中提到的 “转账” 业务场景简述事件溯源的基础工作方式。

采用 CRUD 的方法实现 “转账”。

640?wx_fmt=gif

采用事件溯源的方式实现 “转账”。

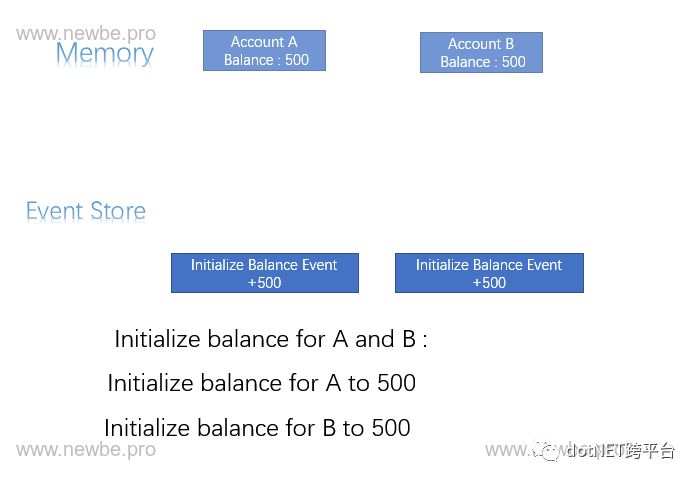
640?wx_fmt=png

如上图所示，通过事件溯源模式将转账业务涉及的余额变动采用事件的方式进行存储。同样也实现了业务本身，而这样却带来了一些好处：

通过事件，可以还原出账号任何阶段的余额，这就一定程度实现了对账号余额的跟踪。
由于两个账号的事件是独立处理的。因此，两个账号的处理速度不会相互影响。例如，账号 B 的转入可能由于需要额外的处理，稍有延迟，但账号 A 仍然可以的转出。
可以通过订阅事件来做一些业务的异步处理。例如：更新数据库中的统计数据，发送短信通知等其他的一些异步操作。

当然引入事件溯源模式之后也就引入了事件溯源相关的一些技术问题。例如：事件所消耗的存储可能较为巨大；不得不应用最终一致性；事件具备不可变性，重构时可能较为困难等。相关的这些问题在一些文章中会有较为细致的说明。读者可以阅读后续的延伸阅读内容，进而进行了解与评估。

系统复杂度是不会因为系统设计变化而减少的，它只是从一个地方转移到了另外的地方。——总说自己菜的月落

让轮子转起来

基于读者已经大体理解了上节理论的基础上，本节将结合上述描述的 “转账” 业务场景，介绍本框架的工作原理。首先读者需要了解一下本框架的两个名词。

Claptrap

640?wx_fmt=gif

Claptrap 是本框架定义的一种特殊 Actor。除了上文中提到 Actor 两种特性之外，Claptrap 还被定义为具有以下特性：

状态由事件进行控制。Actor 的状态在 Actor 内部进行维护。Claptrap 同样也是如此，不过改变 Claptrap 的状态除了在 Actor 之外，还限定其只能通过事件进行改变。这就将事件溯源模式与 Actor 模式进行了结合。通过事件溯源模式保证了 Actor 状态的正确性和可追溯性。这些改变 Claptrap 状态的事件是由 Claptrap 自身产生的。事件产生的原因可以是外部的调用也可以是 Claptrap 内部的类触发器机制产生的。

Minion

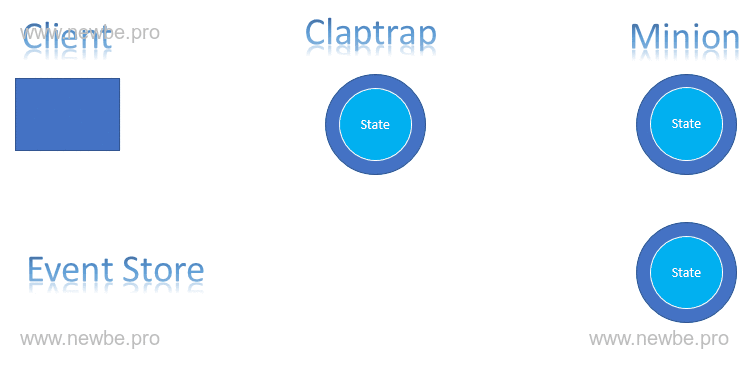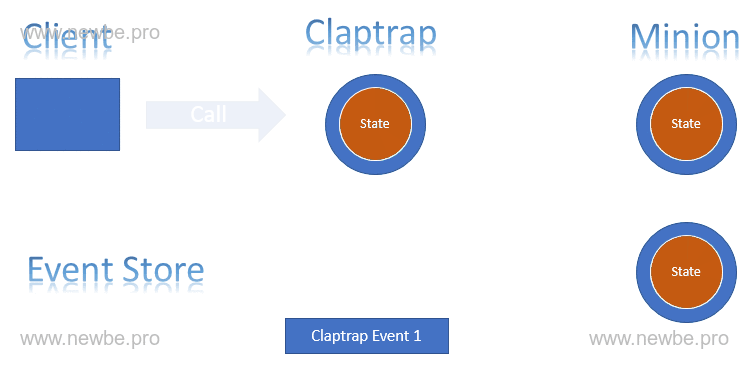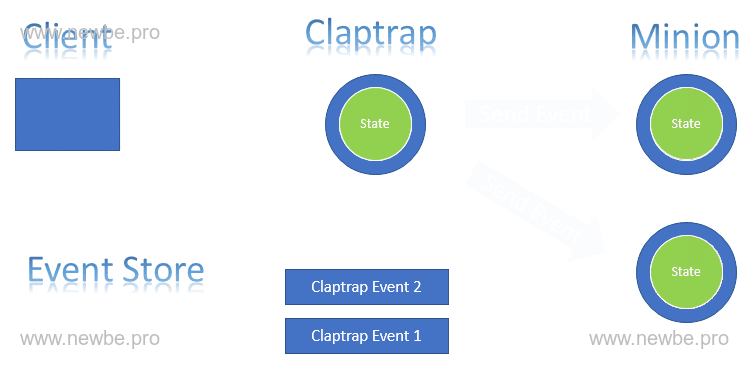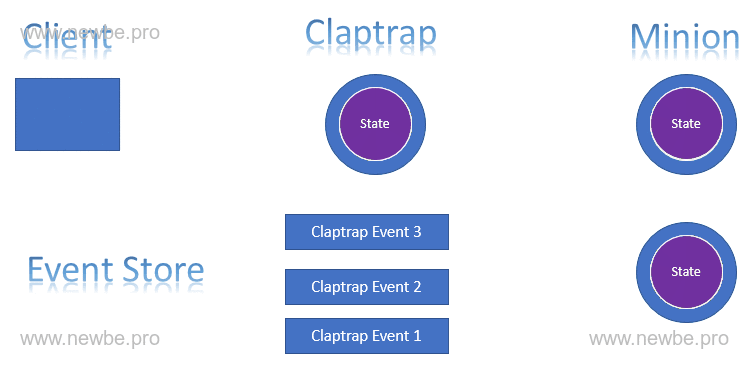
640?wx_fmt=gif

Minion 是本框架定义的一种特殊 Actor。是在 Claptrap 基础上做出的调整。其具备以下特性：

从对应的 Claptrap 读取事件。与 Claptrap 相同，Minion 的状态也由事件进行控制。不同的是，Minion 就像其字面意思一样，总是从对应的 Claptrap 处获取事件，从而改变自身的状态。因此，其可以异步的处理 Claptrap 产生事件之后的后续操作。

业务实现

接下来有了前面的基础介绍，现在介绍一下本框架如何实现上文中的 “转账” 场景。首先可以通过下图来了解一下主要的流程：

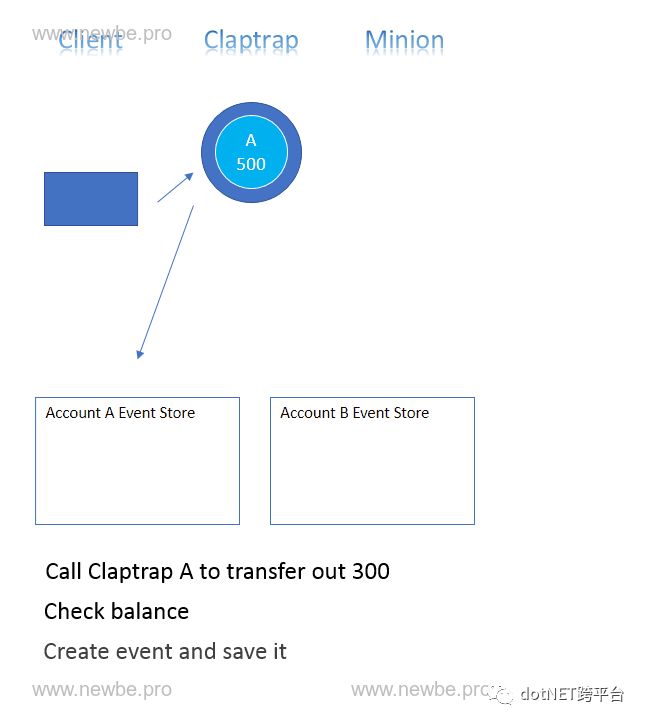
640?wx_fmt=png

如上图所示，整个流程便是本框架实现业务场景的大体过程。另外，还有一些需要指出的是：

图中 Client 与 Claptrap 的调用等待只有第一阶段的时候存在，也就是说，这使得 Client 可以更快的得到响应，不必等待整个流程结束。
Claptrap A 在处理完自身请求，并将事件发送给 Minion A 之后就可以重新接受请求，这样提高了 Claptrap A 的吞吐量。
Minion 不仅仅只能处理 Claptrap 之间的调用代理。在 Minion 当中还可以根据业务需求进行：发送短信，更新数据库统计数据等其他操作。
Minion 也可以具备自己的状态，将部分数据维持在自身的状态中以便外部可以从自身进行查询，而不需要从对应的 Claptrap 中进行查询。例如：统计该账号最近 24 小时的转账变动，以便快速查询。

业务容量

前文提到本框架需要建设的是一个可以水平扩展的系统架构，只有如此才能应对业务容量的持续增长。在这点上，本框架现阶段采用的是微软开源的 Orleans 和 Service Fabric 搭配，实现应用程序和物理设备的放缩。当然，涉及数据存储部分时势必也涉及到数据库集群等一系列问题。这些属于技术应用的细节，而非框架理论设计的内容。因此，此处只表明本框架可以基于以上的开源架构进行容量放缩。应用过程中的实际问题，读者可以在后续的项目内容中寻求解答。