[小技巧]ASP.NET Core中如何预压缩静态文件

原文地址：Pre-compressed static files with ASP.NET Core
作者：Gunnar Peipman
译者：Lamond Lu
译文：https://www.cnblogs.com/lwqlun/p/10552131.html
示例代码：https://github.com/lamondlu/CompressedStaticFileSample

640?wx_fmt=jpeg

Web应用程序的优化是非常重要，因为使用更少的CPU,占用更少的带宽可以减少项目的费用。在ASP.NET Core中我们可以很容易的启用响应压缩，但是针对预压缩文件，就需要做一些额外的功能了。这篇博客文章展示了如何在ASP.NET Core中预压缩静态文件。

为什么需要预压缩文件？

虽然在从服务器请求文件时，我们可以动态压缩文件，但这意味这Web服务器需要做更多的额外工作。其实只有在新的应用程序部署时才会更改要压缩的文件。越好的压缩效果需要CPU做的工作就越多。

这个事实让我们产生一个疑问：是否有可能在不对其进行反复压缩的情况下提供这些文件？幸运的是，这个问题答案是肯定的 - 是的，我们可以在ASP.NET Core中通过扩展静态文件中间件来做到这一点。

创建预压缩文件

为了让整个演示尽量简单，我们可以使用7-Zip来压缩磁盘上的静态文件。以下是压缩默认ASP.NET Core MVC应用程序的site.css文件时7-Zip的对话框窗口。

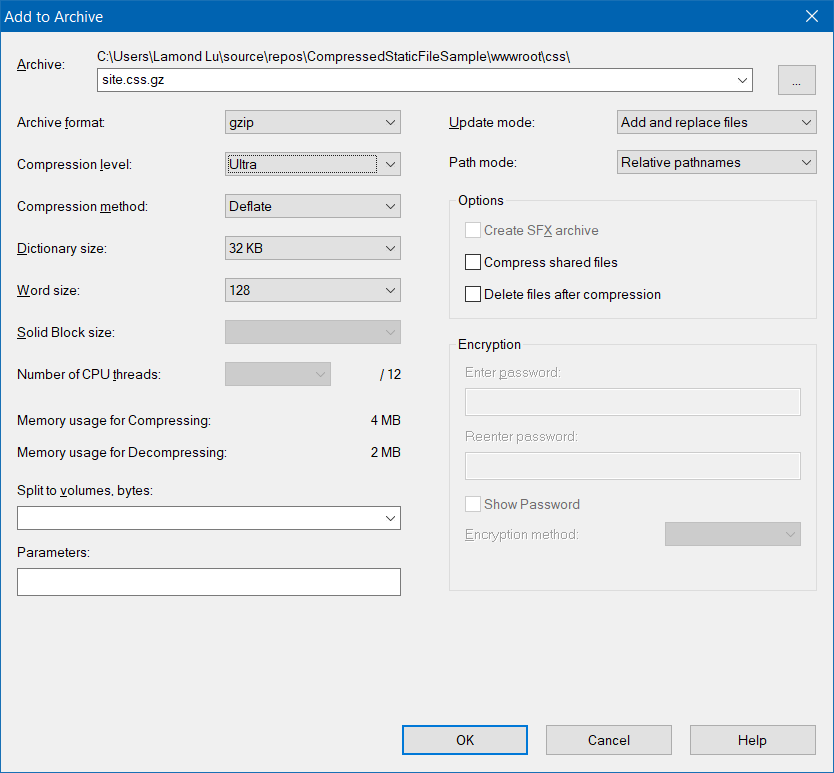
640?wx_fmt=png

这里你可能注意到我启用了 Ultra压缩。这显然不是我们希望在Web服务器上动态压缩的方法，因为它太消耗CPU了。

正常情况下，这里可以使用Gulp来完成文件捆绑和收缩的功能，本文中暂时不会介绍这个。

提供压缩文件

这里我参考了Stack Overflow上的一个简单解决方案（How to gzip static content in ASP.NET Core in a self host environment. ）。它处理了Javascript和CSS文件。

app.UseStaticFiles(new StaticFileOptions
{
OnPrepareResponse = context =>
{
IHeaderDictionary headers = context.Context.Response.Headers;
string contentType = headers["Content-Type"];
if (contentType == "application/x-gzip")
{
if (context.File.Name.EndsWith("js.gz"))
{
contentType = "application/javascript";
}
else if (context.File.Name.EndsWith("css.gz"))
{
contentType = "text/css";
}
headers.Add("Content-Encoding", "gzip");
headers["Content-Type"] = contentType;
}
}
});

当然Javascript和CSS文件并不是唯一需要压缩的文件类型。所以这里我们不能把contentType写死。这里我采用了.NET Core Tutorials站点中提供的一个解决方案（ Getting A Mime Type From A File Name In .NET Core）。对我来说这个方案已经足够简单。

var provider = new FileExtensionContentTypeProvider();
string contentType;
if (!provider.TryGetContentType(fileName, out contentType))
{
contentType = "application/octet-stream";
}

这里我把2个方案合并在里一起，产生了最终解决方案。

var mimeTypeProvider = new FileExtensionContentTypeProvider();
app.UseStaticFiles(new StaticFileOptions
{
OnPrepareResponse = context =>
{
var headers = context.Context.Response.Headers;
var contentType = headers["Content-Type"];
if (contentType != "application/x-gzip" && !context.File.Name.EndsWith(".gz"))
{
return;
}
var fileNameToTry = context.File.Name.Substring(0, context.File.Name.Length - 3);
if (mimeTypeProvider.TryGetContentType(fileNameToTry, out var mimeType))
{
headers.Add("Content-Encoding", "gzip");
headers["Content-Type"] = mimeType;
}
}
});