Hopping Rabbit

题意：

给你n个矩阵，每个矩阵(给出左上标和右下标)，现在让你给出一个点的位置，这个点每次只能上下左右四个方向移动，且移动距离为d，是否存在一个这样的点，其所有落点都不在矩阵内。

题解：

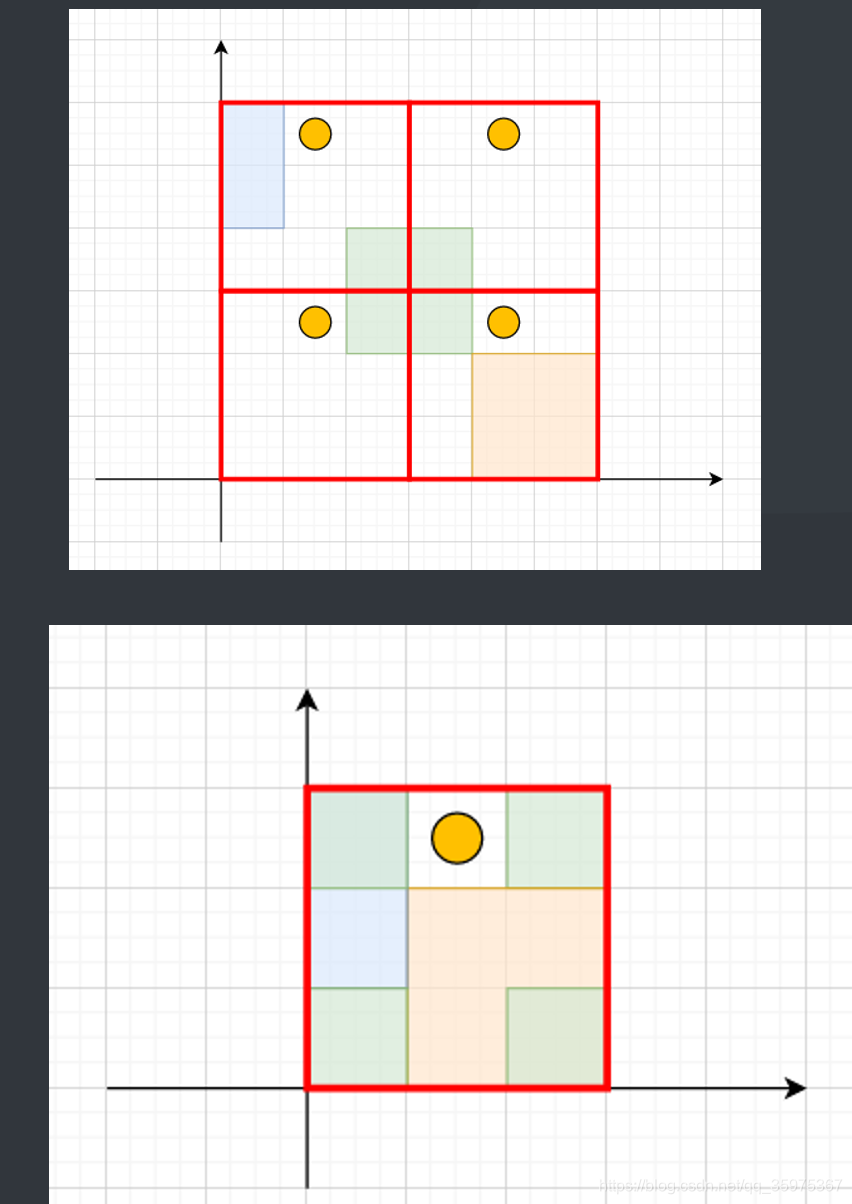
能到达的位置都是周期重复的，比如当前点在(x,y),那么可以到达(x+d,y),(x+2d,y)，所以我们将所有(k1d,k2d)到(k1d+d,k2d+d)范围内的所有图形移动至(1,1)到(d,d)范围内，相当于整体大地图上彼此可以到达的点当作一个点，这样就得到一个d * d的小地图
同样矩阵也会被带到这个小地图，矩阵所覆盖小地图的部分说明在这个位置跳终究会跳到矩阵中，所以我要找是否存在一个点没有被矩阵覆盖。
那问题就变成n个矩阵移动至(1,1)到(d,d)范围内求并，这是扫描先的典型操作。我们用扫描线求每一行的最小值，如果存在0说明有个点没有被覆盖，记录坐标，否在就是全部被覆盖
情况如图：

代码：

#include<bits/stdc++.h>
#define debug(a,b) printf("%s = %d\n",a,b);
using namespace std;
typedef long long ll;
typedef pair<int, int> PII;
clock_t startTime, endTime;
//Fe~Jozky
const ll INF_ll=1e18;
const int INF_int=0x3f3f3f3f;
inline ll read(){ll s=0,w=1ll;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-')w=-1ll;ch=getchar();}while(ch>='0'&&ch<='9') s=s*10ll+((ch-'0')*1ll),ch=getchar();//s=(s<<3)+(s<<1)+(ch^48);return s*w;
}
void rd_test(){#ifdef ONLINE_JUDGE#elsestartTime = clock(); //计时开始freopen("in.txt","r",stdin);#endif
}
void Time_test(){#ifdef ONLINE_JUDGE#elseendTime = clock(); //计时结束printf("\n运行时间为:%lfs\n",(double)(endTime - startTime) / CLOCKS_PER_SEC);#endif
}
const int N=200010;#define lson (id<<1)
#define rson ((id<<1)|1)
#define mid ((l+r)>>1)struct Node
{int val,add,mul;
}tr[N<<2];void push_up(int id,int l,int r)
{tr[id].val=min(tr[lson].val,tr[rson].val);
}void solve(int id,int mul,int add){tr[id].add=tr[id].add*mul+add;tr[id].mul=tr[id].mul*mul;tr[id].val=tr[id].val*mul+add;
}
void push_down(int id){solve(id<<1,tr[id].mul,tr[id].add);solve(id<<1|1,tr[id].mul,tr[id].add);tr[id].mul=1;tr[id].add=0;
}void build(int id,int l,int r)
{tr[id].mul=1;tr[id].add=0;if (l==r){tr[id].val=0;return;}build(lson,l,mid);build(rson,mid+1,r);push_up(id,l,r);
}void update(int id,int l,int r,int L,int R,int mul,int add)
{if (L<=l && R>=r){solve(id,mul,add);return;}push_down(id);if (mid>=R) update(lson,l,mid,L,R,mul,add);else if (mid<L) update(rson,mid+1,r,L,R,mul,add);else{update(lson,l,mid,L,mid,mul,add);update(rson,mid+1,r,mid+1,R,mul,add);}push_up(id,l,r);
}int query(int id,int l,int r,int L,int R)
{if (L<=l && R>=r) return tr[id].val;push_down(id);if (mid>=R) return query(lson,l,mid,L,R);if (mid<L) return query(rson,mid+1,r,L,R);return min(query(lson,l,mid,L,mid),query(rson,mid+1,r,mid+1,R));
}int n,d;
vector<pair<int,int>> add[N],del[N];void upd(int x1,int y1,int x2,int y2)
{int xl=0,xr=0,yl=0,yr=0;if (x2-x1>=d){xl=1;xr=d;}else{xl=(x1%d+d)%d+1;xr=((x2-1)%d+d)%d+1;}if (y2-y1>=d){yl=1;yr=d;}else{yl=(y1%d+d)%d+1;yr=((y2-1)%d+d)%d+1;}if (xl<=xr){if (yl<=yr){add[yl].push_back({xl,xr});del[yr+1].push_back({xl,xr});}else//列拆分成两部分 {add[1].push_back({xl,xr});del[yr+1].push_back({xl,xr});add[yl].push_back({xl,xr});del[d+1].push_back({xl,xr});}}else//行拆分成两部分 {if (yl<=yr){add[yl].push_back({1,xr});add[yl].push_back({xl,d});del[yr+1].push_back({1,xr});del[yr+1].push_back({xl,d});}else{add[1].push_back({1,xr});add[1].push_back({xl,d});del[yr+1].push_back({1,xr});del[yr+1].push_back({xl,d});add[yl].push_back({1,xr});add[yl].push_back({xl,d});del[d+1].push_back({1,xr});del[d+1].push_back({xl,d});}}
}int main()
{scanf("%d%d",&n,&d);int x1=0,y1=0,x2=0,y2=0;for (int i=1;i<=n;i++){scanf("%d%d%d%d",&x1,&y1,&x2,&y2);upd(x1,y1,x2,y2);}build(1,1,d);int ansx=0,ansy=0;for (int y=1;y<=d;y++){for (PII it:add[y]){update(1,1,d,it.first,it.second,1,1);}for (PII it :del[y]){update(1,1,d,it.first,it.second,1,-1);}if (query(1,1,d,1,d)==0)//如果存在空隙，找到空隙坐标 {for (int x=1;x<=d;x++){if (query(1,1,d,x,x)==0){ansx=x;ansy=y;break;}}break;}}if (!ansx) printf("NO\n");else printf("YES\n%d %d\n",ansx-1+d,ansy-1+d);return 0;
}