一、导语
随着大型分布式系统架构的演进和广泛应用,软件工程的最佳实践也随之改变。
我们通过分布式、服务化、DevOps、敏捷开发,快速响应业务的需求变化,支持大规模分布式应用。但这些做法带来效益的同时,也带来了另一个紧迫问题:我们到底有多少把握来确保线上复杂的系统能够正常工作呢?
即便是分布式系统中每个独立的服务都正常工作,服务之间的相互调用也仍然可能造成不可预期的结果。这些结果在现实中可能很少发生,但是一旦发生就会影响整个生产环境,使得整个分布式系统变得混乱不堪,甚至出现服务雪崩、系统全面宕机。
不是由你来选择那一刻,而是那一刻来选择你!
你只能选择为之做好准备。
—消防队长 Mike Burtch因此,我们有必要在线上事故出现之前,提前识别出系统的有哪些弱点、这些弱点的影响范围。我们需要一种方式来管控这些系统的固有混沌,在保证快速响应业务需求变化的同时,做到最后不管系统有多复杂,我们的线上应用经得住各种“戳”。
通过应用一些经验探索的原则,来观察系统是如何反应的。这就跟科学家做实验去学习物理定律一样,通过做实验去了解整个系统。我们从受控的试验中掌握分布式系统运行行为的过程,称为混沌工程。
混沌工程不是制造问题,而是揭示问题。
—Nora Jones,Netflix 高级混沌工程师混沌工程的典型实践-Chaos Monkey,捣乱的猴子;拜 Netflix 所赐,现在大部分的混沌工程项目都叫做 Monkey,也就是一只捣乱的猴子,在你的系统里面上蹦下窜,不停捣乱,直到搞挂你的系统。

为什么需要混沌工程:
应用混沌工程可以提升整个系统的弹性。通过设计并且进行混沌实验,我们可以了解到系统脆弱的一面,在还没出现线上事故之前,我们就能主动发现这些问题,并尽可能的解决这些问题。
混沌工程和测试有什么区别:
虽然混沌工程跟传统测试通常都会共用很多测试工具的,譬如都会使用错误注入工具,但:
混沌工程是通过实践对系统有更新的认知,而传统测试则是使用特定方式对某一块进行特定测试。
譬如在传统测试里面,我们可以写一个断言,我们给定特定的条件,产生一个特定的输出,如果不满足断言条件,测试就出错了,这个其实是具有很明确的特性。但混沌工程是试验,而试验会有怎样的结果,我们是不确定的。
譬如我们可以进行下面的这些试验:
模拟整个 IDC 宕机
选择一部分网络连连接注入特定时间的延迟
随机让一些函数抛出
异常强制 NTP 时间不同步
生成 IO 错误
榨干 CPU
这些混沌试验到底会有什么样的结果,有些我们可以预料,但有些可能我们就不会预先知道,只有发生了,才会惊讶,
“啊,怎么会这样!”
二、混沌工程的方法论
既然是工程,那么就会有方法论,也就能详细的归纳总结出来实施的步骤
1. 混沌工程的一般实施步骤
寻找一些系统正常运行状态下的可度量指标,作为基准的“稳定状态”
假设实验组和对照组都能继续保持这个“稳定状态”
对实验组进行事件注入,如服务器崩溃、硬盘故障、网络连接断开等等
比较实验组和对照组“稳定状态”的差异,推翻上述第2条的假设
如果混沌实验前后保持的“稳定状态”一致,则可以认为系统应对这种故障是弹性的,从而对系统建立更多信心。相反的,如果两者的稳定状态不一致,那我们就找到了一个系统弱点,从而可以修复它,提高系统可靠性。
2. 实施混沌工程的推荐原则
2.1. 根据“稳定状态下系统的特征”做一个假设
以充电为例,充电服务可能包含了订单服务,开启充电、结束充电、电量更新服务,账户服务、计费策略服务,“假设”不是着眼于各个“螺丝钉”服务的具体状态,而是着眼于整个充电系统正常运作下的外部表现(状态),如开启充电TPS、正在充电中订单数、电量更新 TPS、结束充电TPS、充电服务异常等等,这些监控指标曲线一般不会大起大落,其变化趋势是可以预期的。
但是有一点需要特别注意,某些问题虽然不会怎么影响整体监控指标,
但是仍然需要监控系统中各个节点的微观指标(如CPU、IO等)。
2.2 事件是现实世界真的可能发生的
任何可能影响系统稳定状态的都可以作为事件,常见的,如
故障类:像服务器宕机、重启、断网等硬件故障、服务超时、Nginx不可用、核心应用未重启等应用故障;
非故障事件:像流量激增
同时,还可以分析曾经引起系统故障的事件的种类和频次,针对性的排列优先级,并复现这些事件,避免系统再次出现这种故障。
2.3. 在生产环境跑
根据第1条,一般只有生产环境的指标是可预测的,如每日充电订单量、开启充电量、电量更新TPS等。而且,由于测试环境和生产环境不可能一模一样,为了真实反映系统的可靠性,一般推荐在生产环境实施混沌工程。
2.4. 持续集成
线上应用每天都在更新,所以像跑持续集成一样实施混沌工程,持续发现问题、解决问题。
2.5. 最小化影响范围
混沌工程可能导致线上功能不可用,甚至造成宕机事故,所以在以找出系统弱点为目的的前提下,需要最小化故障影响范围,并且当出现严重问题时可以迅速恢复,即故障是可控的。鉴于此,需要控制最小化影响范围。
上面是最理想情况下的混沌工程,现实中我们需要根据现有软件成熟度有阶段的实施混沌:
阶段一:分布式系统弹性化一般
以京东为例,他们会在双十一大促之前进行故障演练,将团队分为两组,一组作为故障的制造者,另外一组作为故障的解决者和响应者,来考察故障发生的时候,团队对故障的检测、响应、处理还有恢复能力。达到小的故障不需要人介入,大故障人工介入可以快速处理的目的。通过在大促之前的两个月期间密集的开展混沌工程,提高团队对大规模故障的容错能力。
阶段二:分布式系统弹性化成熟
以Netflix为例,他们基本上已经在按照上述理想的步骤和原则实施混沌工程,工作日持续、自动的实施混沌工程,系统具备高度的可靠性,弹性伸缩。
三、混沌工程的成熟度模型
混沌工程成熟度模型,Netflix (网飞)总结了两个维度,一个是复杂度,一个就是接受度。
前者表示的是混沌工程能有多复杂,而后者则表示的是混沌工程被团队的接受程度。
复杂度分为哪几个阶段:
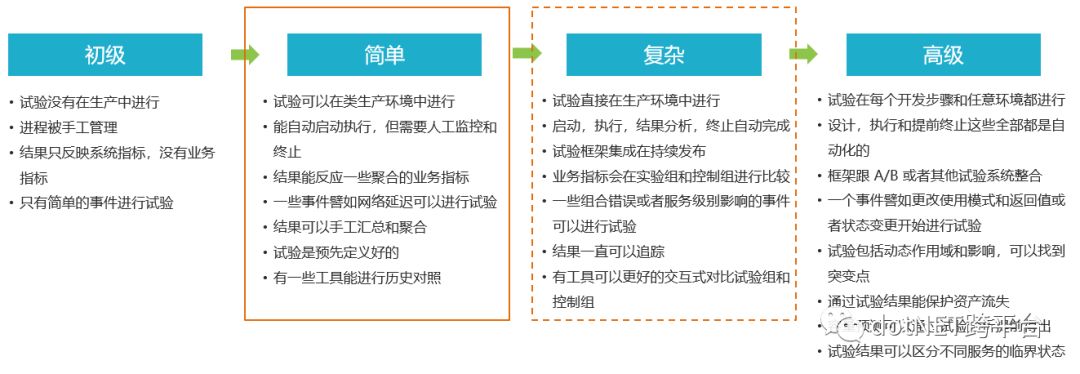
接受度分为哪几个阶段:
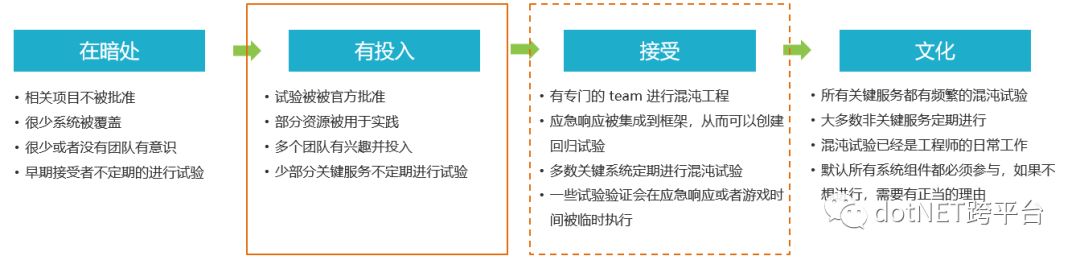
我们目前处于起步发展阶段,线上生产环境实施混沌工程,风险很大,也不可控,因此:
我们在压测模拟环境实施混沌工程,搭建类似生产的小型模拟环境,以正常、合理的测试结果,作为基准“稳定状态”。在模拟测试的过程中,对系统实施各类混沌实验后,通过观察测试结果来评估系统的可靠性,从而寻找系统弱点,
登记Bug,进行修复。
同时,通过自动化运维平台,实现混沌实验异常注入和持续执行。
四、混沌工程的执行
1. 混沌工程的整体实施流程
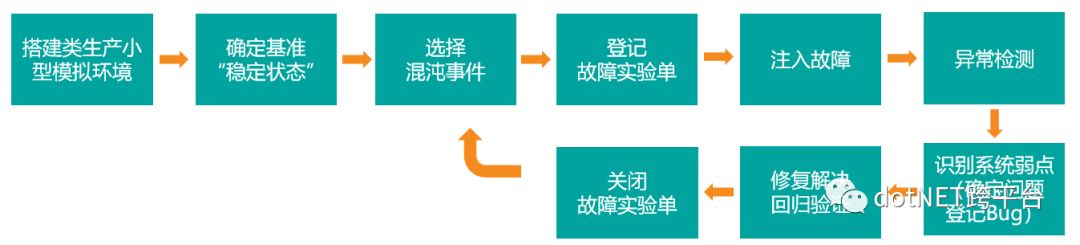
2. 混沌事件注入
应用层的混沌事件
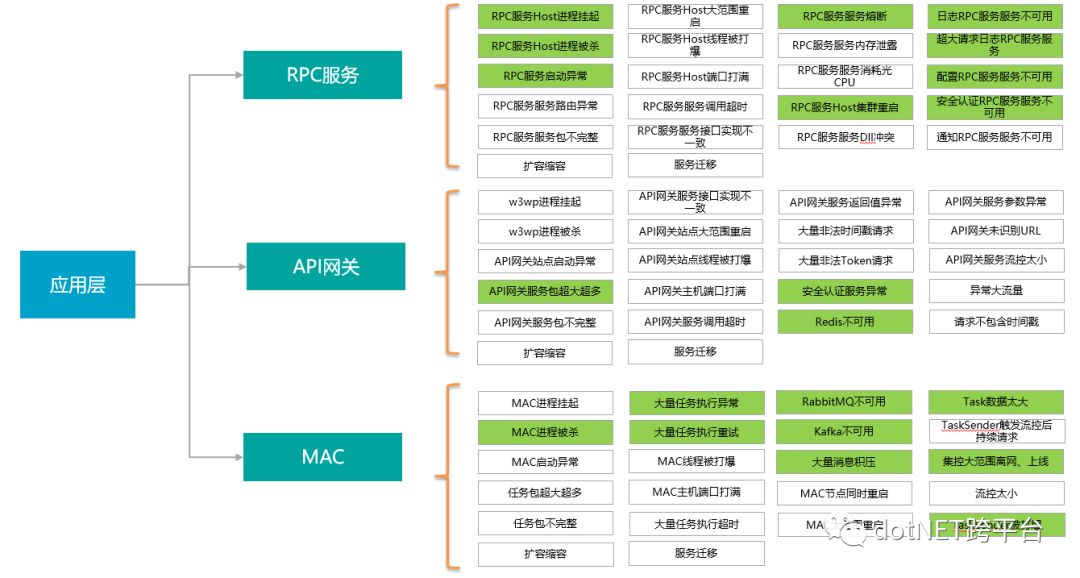
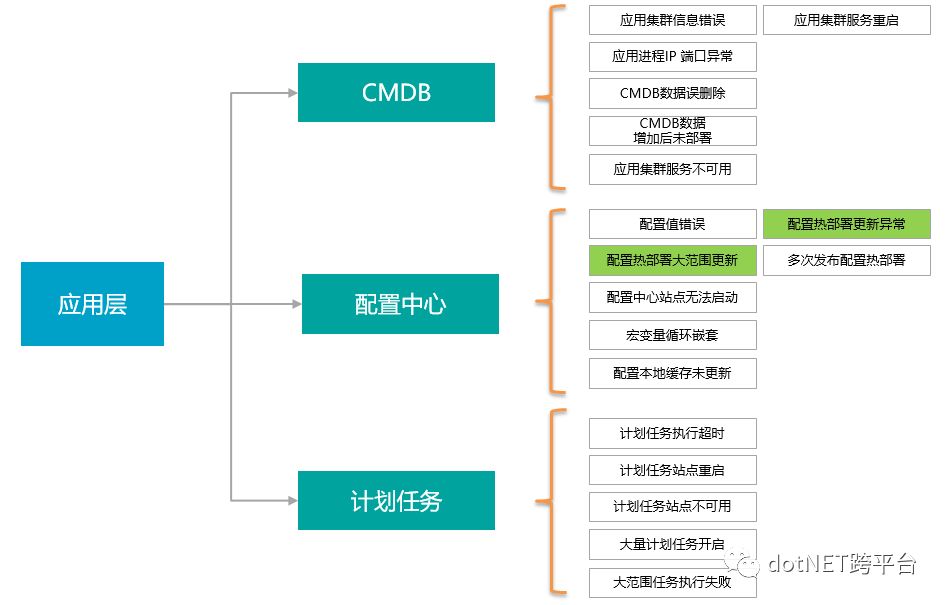
中间件层混沌事件
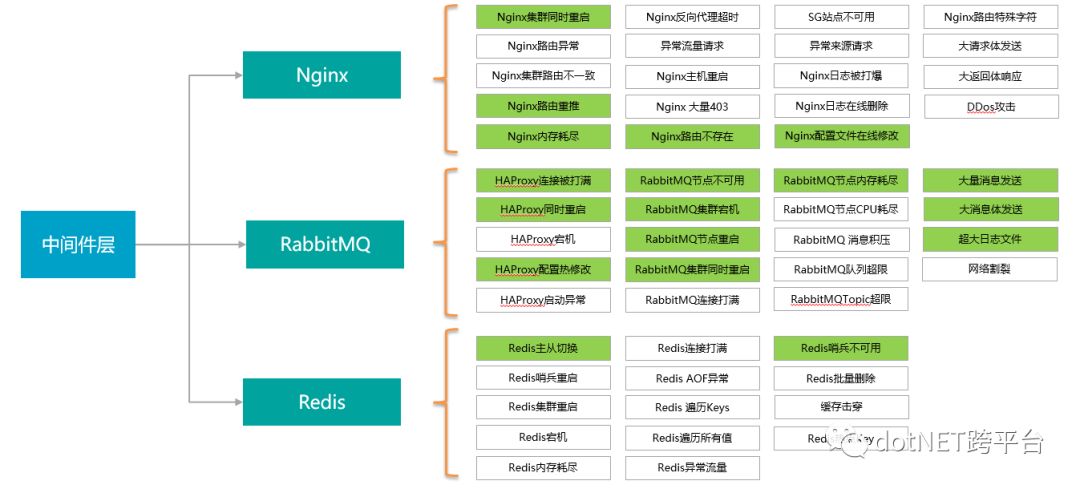
数据库层和基础实施层混沌事件

3. 混沌实验闭环
所有的混沌实验必须实现闭环,发现问题,分析问题,解决问题
因此我们增加了一类单据统一管理混沌实验,便于总结、分析、跟踪
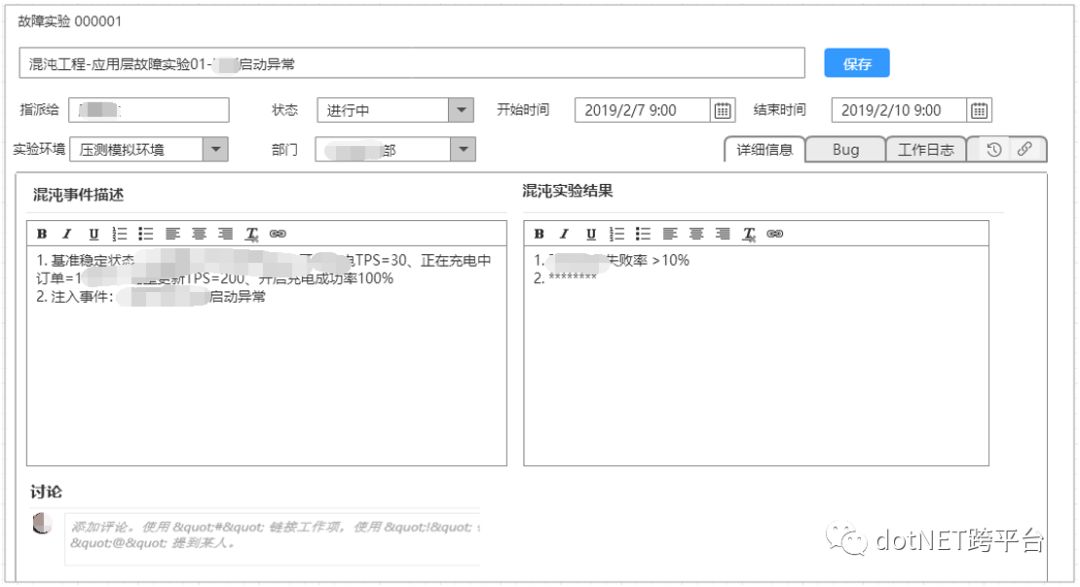
以上是我们今年搞混沌工程,提升系统可用性的一些实践,分享给大家。
![[ZJOI2007] 棋盘制作(单调栈 / DP悬线法)](http://pic.xiahunao.cn/[ZJOI2007] 棋盘制作(单调栈 / DP悬线法))
![P2567 [SCOI2010]幸运数字](http://pic.xiahunao.cn/P2567 [SCOI2010]幸运数字)

![[ZJOI2007] 时态同步(拓扑序)](http://pic.xiahunao.cn/[ZJOI2007] 时态同步(拓扑序))
![P2571 [SCOI2010]传送带](http://pic.xiahunao.cn/P2571 [SCOI2010]传送带)
)
![[ZJOI2007]报表统计(链表法+set)](http://pic.xiahunao.cn/[ZJOI2007]报表统计(链表法+set))
)

)
![[ZJOI2008]泡泡堂(田忌赛马贪心)](http://pic.xiahunao.cn/[ZJOI2008]泡泡堂(田忌赛马贪心))
)
![[ZJOI2010] 基站选址(线段树优化dp)](http://pic.xiahunao.cn/[ZJOI2010] 基站选址(线段树优化dp))

)
![[ZJOI2010] 贪吃的老鼠(二分+差分+神仙建图网络流)](http://pic.xiahunao.cn/[ZJOI2010] 贪吃的老鼠(二分+差分+神仙建图网络流))


![[TJOI2012] 旅游(树的直径)](http://pic.xiahunao.cn/[TJOI2012] 旅游(树的直径))
:Python条件判断)