problem

洛谷链接

solution1-单调栈

很容易想到，预处理出每个点向上最大能延伸的长度，然后对每个点求一个矩阵面积。

然后思考优化，不难想到每次对一行进行求解。

每一行的所有列一起构成了一个直方图。

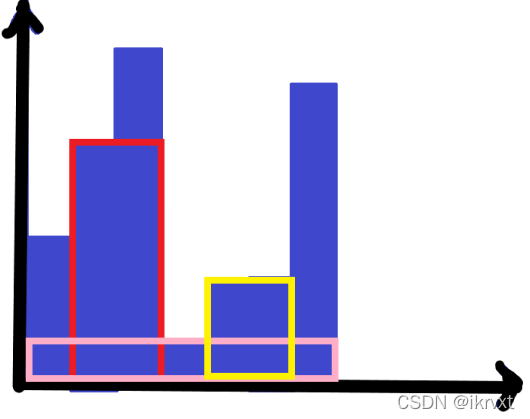
直方图直接经典笛卡尔树。笛卡尔树性质是什么？是单调栈！

直接对每一行都建一个单调栈，遍历列维护递增栈，弹出时计算答案。正方形将两边取个 $\min$ 再比就行了。

这个做法很简单，但是直观上是 $O(n^3)$ 的，所以很多人不敢打。

但实际上跑很快，因为每个点只会被做一次。一次单调栈是做连续一段。

时间复杂度应该是 $O(n^2)$ 的。

#include <bits/stdc++.h>
using namespace std;
#define maxn 2005
int n, m, top, ans1, ans2;
int h[maxn], s[maxn];
int c[maxn][maxn];int main() {scanf( "%d %d", &n, &m );for( int i = 1;i <= n;i ++ )for( int j = 1;j <= m;j ++ )scanf( "%d", &c[i][j] );for( int i = 1;i <= n;i ++ ) { //枚举每一行for( int j = 1;j <= m;j ++ ) //预处理该行上每一列最长能向上延伸的长度if( i > 1 and c[i][j] ^ c[i - 1][j] ) ++ h[j];else h[j] = 1;for( int j = 1, k;j <= m;j = k ) {s[0] = j - 1, s[top = 1] = j;for( k = j + 1;k <= m and c[i][k] ^ c[i][k - 1];k ++ ) {while( top and h[s[top]] > h[k] ) {ans1 = max( ans1, min(h[s[top]], k - s[top - 1] - 1) * min(h[s[top]], k - s[top - 1] - 1) );ans2 = max( ans2, h[s[top]] * (k - s[top - 1] - 1) );top --;}s[++ top] = k;}while( top ) {ans1 = max( ans1, min(h[s[top]], k - s[top - 1] - 1) * min(h[s[top]], k - s[top - 1] - 1) );ans2 = max( ans2, h[s[top]] * (k - s[top - 1] - 1) );top --;}}}printf( "%d\n%d\n", ans1, ans2 );return 0;
}

solution2-DP悬线法

最大子矩阵很熟悉啊！是 $DP$ 入门必讲的经典例题。

对每一个位置 $(i,j)$ 预处理出其向上/向左/向右分别能延伸到多远。

然后询问每一个位置 $(i,j)$ 被包含的最大子矩阵，如果和上一行是合法的就要结合上一行的左右限制。

具体而言，左边限制取较大值，右边限制取较小值，本质是取最靠近 $(i,j)$ 的左右两边限制。

取完后，矩形长即 $r(i,j)-l(i,j)+1$，宽即 $h(i,j)$。就可以求了。

这里需要注意的是，不能在预处理的时候，就考虑上一行的左右限制。

//这么写就是错的
for( int i = 1;i <= n;i ++ )for( int j = 1;j <= m;j ++ )if( j > 1 and c[i][j] ^ c[i][j - 1] )if( h[i][j] > 1 ) l[i][j] = max( l[i - 1][j], l[i][j - 1] );else l[i][j] = l[i][j - 1];else l[i][j] = j;
for( int i = 1;i <= m;i ++ ) r[0][i] = m;
for( int i = 1;i <= n;i ++ )for( int j = m;j;j -- )if( j < m and c[i][j] ^ c[i][j + 1] )if( h[i][j] > 1 ) r[i][j] = min( r[i - 1][j], r[i][j + 1] );else r[i][j] = r[i][j + 1];else r[i][j] = j;

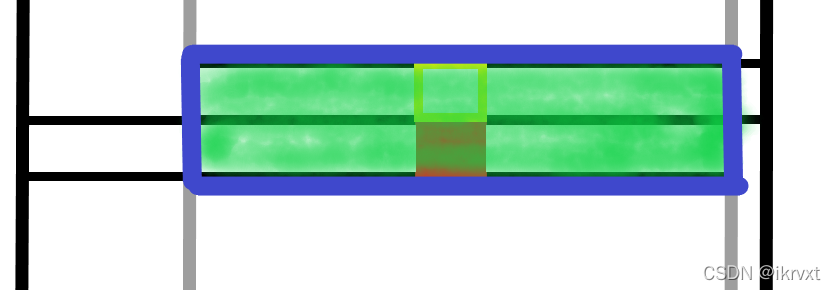
你过早的刻画了左右边界，就会出现上面这种。虽然对于紫红色点而言确实是这个矩形。

但对于后面的黄色点而言，其递推的左边界也被限制在了黑线处，就算不到红色矩形了。

#include <bits/stdc++.h>
using namespace std;
#define maxn 2005
int n, m;
int c[maxn][maxn], h[maxn][maxn], l[maxn][maxn], r[maxn][maxn];int main() {scanf( "%d %d", &n, &m );for( int i = 1;i <= n;i ++ )for( int j = 1;j <= m;j ++ )scanf( "%d", &c[i][j] );for( int i = 1;i <= n;i ++ )for( int j = 1;j <= m;j ++ )if( i > 1 and c[i][j] ^ c[i - 1][j] ) h[i][j] = h[i - 1][j] + 1;else h[i][j] = 1;for( int i = 1;i <= n;i ++ )for( int j = 1;j <= m;j ++ )if( j > 1 and c[i][j] ^ c[i][j - 1] ) l[i][j] = l[i][j - 1];else l[i][j] = j;for( int i = 1;i <= n;i ++ )for( int j = m;j >= 1;j -- )if( j < m and c[i][j] ^ c[i][j + 1] ) r[i][j] = r[i][j + 1];else r[i][j] = j;int ans1 = 0, ans2 = 0;for( int i = 1;i <= n;i ++ )for( int j = 1;j <= m;j ++ ) {if( i > 1 and c[i][j] ^ c[i - 1][j] ) {l[i][j] = max( l[i][j], l[i - 1][j] );r[i][j] = min( r[i][j], r[i - 1][j] );}ans1 = max( ans1, min( r[i][j] - l[i][j] + 1, h[i][j] ) * min( r[i][j] - l[i][j] + 1, h[i][j] ) );ans2 = max( ans2, ( r[i][j] - l[i][j] + 1 ) * h[i][j] );}printf( "%d\n%d\n", ans1, ans2 );return 0;
}