problem

给定一个 $n$ 个点，$m$ 条边的无向连通图，图有边权，每个点有一个颜色。

有 $q$ 次操作，每次操作可更改某一个点颜色。

求每次操作后图中不同颜色点之间的最短距离。

若图中点颜色全相同，输出 $0$。

一行给定 $n,m,c,q$。接下来 $m$ 行形如 $(u,v,w)$，表示 $u,v$ 间有一条边长 $w$。

接下来一行 $n$ 个数表示颜色。最后 $q$ 行，每行形如 $x,y$，把 $x$ 点颜色改为 $y$。

$c\le n\le 2e5,m\le 3e5,q\le 2e5,1\le w\le 1e6$。

solution

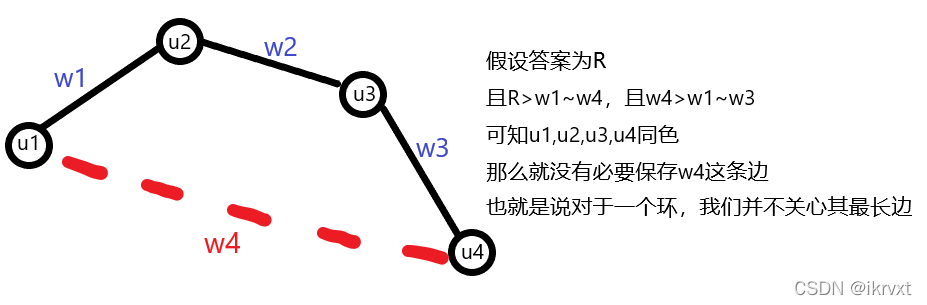
observation：因为 $w$ 是正的，所以答案一定是某条边的权值。

observation：这条边一定在图的随便一棵 $\text{MST}$（最小生成树）上。

只要发现了这两个性质，这道题就转化成了求树上任意两异色相邻点的最短距离。

我们考虑每个点对答案的贡献，即求出这个点儿子中距离最近且与之异色的儿子。

怎么快速求得？

• 将该点的所有儿子扔到线段树上，线段树合并颜色信息。

  具体而言，如果两段相邻颜色不同，合并后颜色赋零，否则赋成同样颜色。

  并且儿子要按照距离该点的距离有序排列重编号后再以重编号建线段树。

  直接在线段树上走与该点颜色不同的区间，先走左儿子（距离最近）。

  动态开点哦~

然后将所有点对答案的贡献放到一个优先队列里面，最短距离就从这中间产生。

现在考虑修改某个点颜色后的变化。显然只会影响该点的贡献以及该点父亲的贡献。

• 该点贡献。直接在其对应线段树上重新以新颜色为标准找即可。

• 该点父亲贡献。直接在父亲对应线段上修改该点的信息，然后父亲再查一遍。

• 将两者产生的新贡献直接覆盖原来的贡献。

  具体而言：可以开一个数组记录每个点实时贡献，最后输出最短距离时候判断一下存的贡献和对应点现在提供的贡献是否相同。不同扔掉即可。

时间复杂度就只带个 $\log$ 。

code

#include <bits/stdc++.h>
using namespace std;
#define maxn 200005
#define maxm 300005
#define inf 0x3f3f3f3f
#define Pair pair < int, int >
struct edge { int u, v, w; }E[maxm];
vector < Pair > G[maxn];
priority_queue < Pair, vector < Pair >, greater < Pair > > ans;
int n, m, C, Q, cnt;
int c[maxn];
int head[maxn], to[maxn], nxt[maxn], len[maxn];
int f[maxn], dis[maxn], siz[maxn], id[maxn];int find( int x ) {return x == f[x] ? x : f[x] = find( f[x] );
}void addedge( int u, int v, int w ) {len[cnt] = w, to[cnt] = v, nxt[cnt] = head[u], head[u] = cnt ++;
}void dfs( int u, int fa ) {f[u] = fa;for( int i = head[u];~ i;i = nxt[i] )if( to[i] ^ fa ) {dfs( to[i], u );G[u].push_back( make_pair( len[i], to[i] ) );siz[u] ++;}sort( G[u].begin(), G[u].end() );for( int i = 1;i <= siz[u];i ++ ) id[G[u][i - 1].second] = i;//根据排序 对于u而言 id越小的儿子离u越近//所以在线段树上尽可能往左走
}int root[maxn];
namespace sgt {struct node { int lson, rson, color; }t[maxn * 30];#define lson t[now].lson#define rson t[now].rson#define mid (l + r >> 1)void pushup( int now ) {if( ! lson ) t[now].color = t[rson].color;else if( ! rson ) t[now].color = t[lson].color;else {if( t[lson].color ^ t[rson].color ) t[now].color = 0;else t[now].color = t[rson].color;}}void modify( int &now, int l, int r, int pos, int col ) {if( ! now ) now = ++ cnt;if( l == r ) { t[now].color = col; return; }if( pos <= mid ) modify( lson, l, mid, pos, col );else modify( rson, mid + 1, r, pos, col );pushup( now );}int query( int now, int l, int r, int col ) {if( t[now].color == col ) return inf;if( l == r ) return l;if( t[lson].color ^ col ) return query( lson, l, mid, col );//先找左else return query( rson, mid + 1, r, col );  }
}int main() {scanf( "%d %d %d %d", &n, &m, &C, &Q );for( int i = 1, u, v, w;i <= m;i ++ ) {scanf( "%d %d %d", &u, &v, &w );if( u == v ) continue;E[i] = (edge){ u, v, w };}for( int i = 1;i <= n;i ++ ) scanf( "%d", &c[i] );sort( E + 1, E + m + 1, []( edge x, edge y ) { return x.w < y.w; } );iota( f + 1, f + n + 1, 1 );memset( head, -1, sizeof( head ) );for( int i = 1;i <= m;i ++ ) {int u = E[i].u, v = E[i].v, w = E[i].w;int fu = find( u ), fv = find( v );if( fu ^ fv ) {f[fv] = fu;addedge( u, v, w );addedge( v, u, w );}}dfs( 1, 0 ); cnt = 0;//对每个点 将其所有儿子建成一棵线段树 上面储存颜色信息for( int i = 2;i <= n;i ++ ) sgt :: modify( root[f[i]], 1, siz[f[i]], id[i], c[i] );for( int i = 1;i <= n;i ++ )if( siz[i] ) {int w = sgt :: query( root[i], 1, siz[i], c[i] );if( w == inf ) dis[i] = inf;else dis[i] = G[i][w - 1].first, ans.push( make_pair( dis[i], i ) );//儿子重编号是1~siz[i]对应vector的下标都要-1}for( int i = 1, x, y;i <= Q;i ++ ) {scanf( "%d %d", &x, &y );c[x] = y;if( siz[x] ) {//改和儿子间的答案int w = sgt :: query( root[x], 1, siz[x], c[x] );if( w == inf ) dis[x] = inf;else if( dis[x] != G[x][w - 1].first ) {dis[x] = G[x][w - 1].first;ans.push( make_pair( dis[x], x ) );}}if( f[x] ) {//改和父亲的答案sgt :: modify( root[f[x]], 1, siz[f[x]], id[x], c[x] ); //在父亲的线段树上修改x的信息int w = sgt :: query( root[f[x]], 1, siz[f[x]], c[f[x]] );if( w == inf ) dis[f[x]] = inf;else if( dis[f[x]] != G[f[x]][w - 1].first ) {dis[f[x]] = G[f[x]][w - 1].first;ans.push( make_pair( dis[f[x]], f[x] ) );}}while( ! ans.empty() ) {//有些点颜色改变信息不再正确 通过一直是正确的dis来弹出错误备选答案if( dis[ans.top().second] ^ ans.top().first ) ans.pop();else break;}if( ans.empty() ) puts("0");else printf( "%d\n", ans.top().first );}return 0;
}