都知道反射伤性能，但不得不反射的时候又怎么办呢？当真的被问题逼迫的时候还是能找到解决办法的。

为反射得到的方法创建一个委托，此后调用此委托将能够提高近乎直接调用方法本身的性能。（当然 Emit 也能够帮助我们显著提升性能，不过直接得到可以调用的委托不是更加方便吗？）

---

性能对比数据

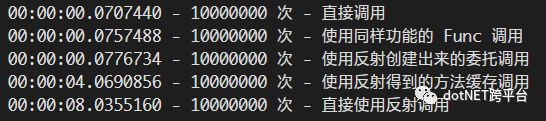
▲ 没有什么能够比数据更有说服力（注意后面两行是有秒数的）

可能我还需要解释一下那五行数据的含义：

1. 直接调用（?应该没有什么比直接调用函数本身更有性能优势的吧）

2. 做一个跟直接调用的方法功能一模一样的委托（?目的是看看调用委托相比调用方法本身是否有性能损失，从数据上看，损失非常小）

3. 本文重点 将反射出来的方法创建一个委托，然后调用这个委托（?看看吧，性能跟直接调差别也不大嘛）

4. 先反射得到方法，然后一直调用这个方法（?终于可以看出来反射本身还是挺伤性能的了，50 多倍的性能损失啊）

5. 缓存都不用，从头开始反射然后调用得到的方法（?100 多倍的性能损失了）

以下是测试代码，可以更好地理解上图数据的含义：

using System;
using System.Diagnostics;
using System.Reflection;

namespace Walterlv.Demo
{
    public class Program
    {
        static void Main(string[] args)
        {
            // 调用的目标实例。
            var instance = new StubClass();

            // 使用反射找到的方法。
            var method = typeof(StubClass).GetMethod(nameof(StubClass.Test), new[] { typeof(int) });

            // 将反射找到的方法创建一个委托。
            var func = InstanceMethodBuilder<int, int>.CreateInstanceMethod(instance, method);

            // 跟被测方法功能一样的纯委托。
            Func<int, int> pureFunc = value => value;

            // 测试次数。
            var count = 10000000;

            // 直接调用。
            var watch = new Stopwatch();
            watch.Start();
            for (var i = 0; i < count; i++)
            {
                var result = instance.Test(5);
            }

            watch.Stop();
            Console.WriteLine($"{watch.Elapsed} - {count} 次 - 直接调用");

            // 使用同样功能的 Func 调用。
            watch.Restart();
            for (var i = 0; i < count; i++)
            {
                var result = pureFunc(5);
            }

            watch.Stop();
            Console.WriteLine($"{watch.Elapsed} - {count} 次 - 使用同样功能的 Func 调用");

            // 使用反射创建出来的委托调用。
            watch.Restart();
            for (var i = 0; i < count; i++)
            {
                var result = func(5);
            }

            watch.Stop();
            Console.WriteLine($"{watch.Elapsed} - {count} 次 - 使用反射创建出来的委托调用");

            // 使用反射得到的方法缓存调用。
            watch.Restart();
            for (var i = 0; i < count; i++)
            {
                var result = method.Invoke(instance, new object[] { 5 });
            }

            watch.Stop();
            Console.WriteLine($"{watch.Elapsed} - {count} 次 - 使用反射得到的方法缓存调用");

            // 直接使用反射调用。
            watch.Restart();
            for (var i = 0; i < count; i++)
            {
                var result = typeof(StubClass).GetMethod(nameof(StubClass.Test), new[] { typeof(int) })
                    ?.Invoke(instance, new object[] { 5 });
            }

            watch.Stop();
            Console.WriteLine($"{watch.Elapsed} - {count} 次 - 直接使用反射调用");
        }

        private class StubClass
        {
            public int Test(int i)
            {
                return i;
            }
        }
    }
}

上面的代码中，有一个我们还没有实现的 InstanceMethodBuilder 类型，接下来将介绍如何实现它。

如何实现

实现的关键就在于 MethodInfo.CreateDelegate 方法。这是 .NET Standard 中就有的方法，这意味着 .NET Framework 和 .NET Core 中都可以使用。

此方法有两个重载：

• 要求传入一个类型，而这个类型就是应该转成的委托的类型

• 要求传入一个类型和一个实例，一样的，类型是应该转成的委托的类型

他们的区别在于前者创建出来的委托是直接调用那个实例方法本身，后者则更原始一些，真正调用的时候还需要传入一个实例对象。

拿上面的 StubClass 来说明会更直观一些：

private class StubClass
{
    public int Test(int i)
    {
        return i;
    }
}

前者得到的委托相当于 int Test(int i) 方法，后者得到的委托相当于 int Test(StubClass instance, int i) 方法。（在 IL 里实例的方法其实都是后者，而前者更像 C# 中的代码，容易理解。）

单独使用 CreateDelegate 方法可能每次都需要尝试第一个参数到底应该传入些什么，于是我将其封装成了泛型版本，增加易用性。

using System;
using System.Linq;
using System.Reflection;
using System.Diagnostics.Contracts;

namespace Walterlv.Demo
{
    public static class InstanceMethodBuilder<T, TReturnValue>
    {
        /// <summary>
        /// 调用时就像 var result = func(t)。
        /// </summary>
        [Pure]
        public static Func<T, TReturnValue> CreateInstanceMethod<TInstanceType>(TInstanceType instance, MethodInfo method)
        {
            if (instance == null) throw new ArgumentNullException(nameof(instance));
            if (method == null) throw new ArgumentNullException(nameof(method));

            return (Func<T, TReturnValue>) method.CreateDelegate(typeof(Func<T, TReturnValue>), instance);
        }

        /// <summary>
        /// 调用时就像 var result = func(this, t)。
        /// </summary>
        [Pure]
        public static Func<TInstanceType, T, TReturnValue> CreateMethod<TInstanceType>(MethodInfo method)
        {
            if (method == null)
                throw new ArgumentNullException(nameof(method));

            return (Func<TInstanceType, T, TReturnValue>) method.CreateDelegate(typeof(Func<TInstanceType, T, TReturnValue>));
        }
    }
}

泛型的多参数版本可以使用泛型类型生成器生成，我在 生成代码，从 <T> 到 <T1, T2, Tn> —— 自动生成多个类型的泛型 - 吕毅 一文中写了一个泛型生成器，可以稍加修改以便适应这种泛型类。

原文地址：https://blog.walterlv.com/post/create-delegate-to-improve-reflection-performance.html 

.NET社区新闻，深度好文，欢迎访问公众号文章汇总 http://www.csharpkit.com