Display Substring

题意：

一个长度为n的字符串，每个字符有自己的价值，求第k小价值的不重复子串价值

题解：

首先众所周知，所有子串都可以用后缀的前缀来表示，这就和后缀数组扯上关系了
我们可以直接二分这个价值val，然后去算大于val的不重复子串有多少个(比如有x个)，如果x大于k，说明该价值的情况下存在第k小价值，那r可以缩小，否则l可以增大，这是二分过程
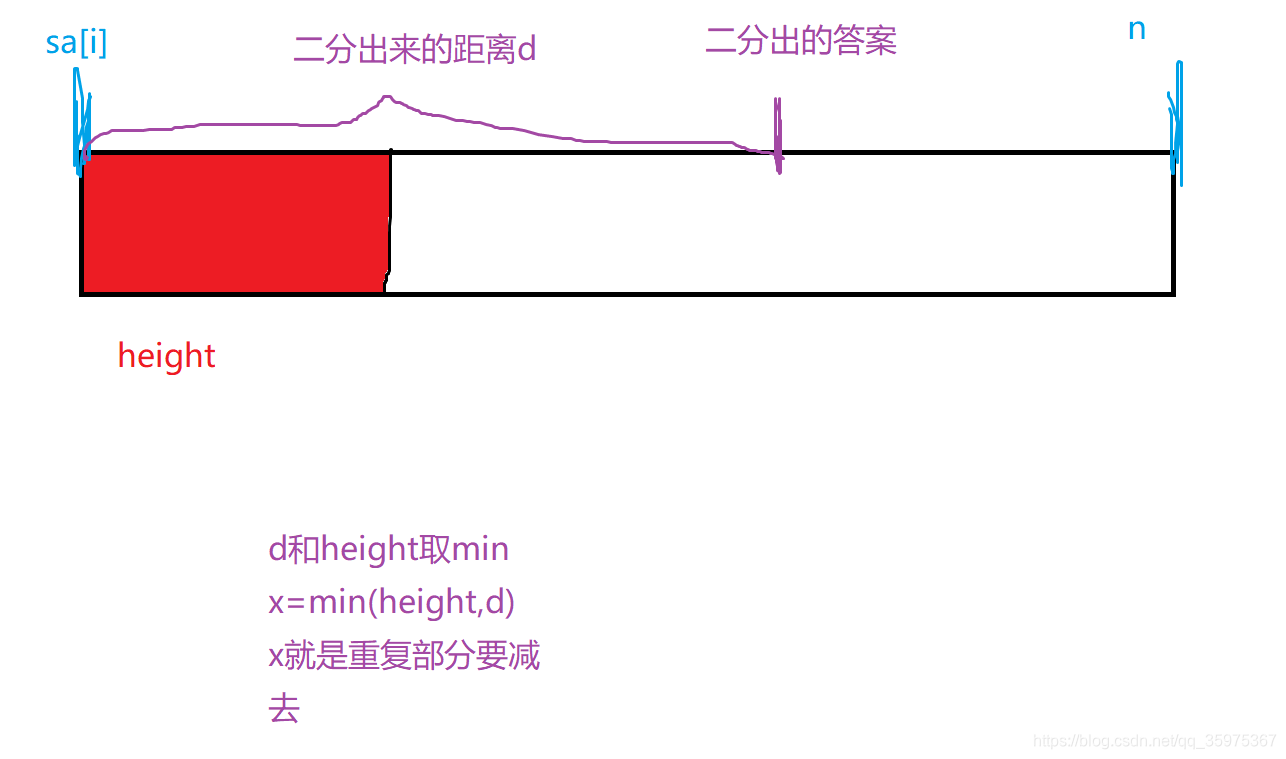
那如果计算大于val的不重复子串有多少个，遍历后缀数组，对于每个后缀，如果其越长说明其价值越高,符合单调性，所有我们二分(没错二分套二分)，二分找到价值小于等于val的值的前缀有多少个，再减去重复部分，看是否大于k，如果大于第一个二分就返回true
重复部分就是height数组对应的值，通过这题可以知道P2408 不同子串个数
注意height要和后缀二分出来的距离取min，因为要删除重复部分不能比这个字符串的长度还长

代码：

// Problem: Display Substring
// Contest: HDOJ
// URL: https://acm.hdu.edu.cn/showproblem.php?pid=6988
// Memory Limit: 262 MB
// Time Limit: 8000 ms
// Data:2021-08-22 17:57:49
// By Jozky#include <bits/stdc++.h>
#include <unordered_map>
#define debug(a, b) printf("%s = %d\n", a, b);
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> PII;
clock_t startTime, endTime;
//Fe~Jozky
const ll INF_ll= 1e18;
const int INF_int= 0x3f3f3f3f;
void read(){};
template <typename _Tp, typename... _Tps> void read(_Tp& x, _Tps&... Ar)
{x= 0;char c= getchar();bool flag= 0;while (c < '0' || c > '9')flag|= (c == '-'), c= getchar();while (c >= '0' && c <= '9')x= (x << 3) + (x << 1) + (c ^ 48), c= getchar();if (flag)x= -x;read(Ar...);
}
template <typename T> inline void write(T x)
{if (x < 0) {x= ~(x - 1);putchar('-');}if (x > 9)write(x / 10);putchar(x % 10 + '0');
}
void rd_test()
{
#ifdef LOCALstartTime= clock();freopen("in.txt", "r", stdin);
#endif
}
void Time_test()
{
#ifdef LOCALendTime= clock();printf("\nRun Time:%lfs\n", (double)(endTime - startTime) / CLOCKS_PER_SEC);
#endif
}
const int MAXN= 3e5;char ch[MAXN], all[MAXN];
int sa[MAXN], rk[MAXN], height[MAXN], tax[MAXN], tp[MAXN], a[MAXN], n, m;
char str[MAXN];
//rk[i] 第i个后缀的排名; sa[i] 排名为i的后缀位置; height[i] 排名为i的后缀与排名为(i-1)的后缀的LCP
//tax[i] 计数排序辅助数组; tp[i] rk的辅助数组(计数排序中的第二关键字),与sa意义一样。
//a为原串
void RSort()
{//rk第一关键字,tp第二关键字。for (int i= 0; i <= m; i++)tax[i]= 0;for (int i= 1; i <= n; i++)tax[rk[tp[i]]]++;for (int i= 1; i <= m; i++)tax[i]+= tax[i - 1];for (int i= n; i >= 1; i--)sa[tax[rk[tp[i]]]--]= tp[i]; //确保满足第一关键字的同时，再满足第二关键字的要求
} //计数排序,把新的二元组排序。int cmp(int* f, int x, int y, int w)
{return f[x] == f[y] && f[x + w] == f[y + w];
}
//通过二元组两个下标的比较，确定两个子串是否相同void Suffix()
{//safor (int i= 1; i <= n; i++)rk[i]= a[i], tp[i]= i;m= 127, RSort(); //一开始是以单个字符为单位，所以(m = 127)for (int w= 1, p= 1, i; p < n; w+= w, m= p) { //把子串长度翻倍,更新rk//w 当前一个子串的长度; m 当前离散后的排名种类数//当前的tp(第二关键字)可直接由上一次的sa的得到for (p= 0, i= n - w + 1; i <= n; i++)tp[++p]= i; //长度越界,第二关键字为0for (i= 1; i <= n; i++)if (sa[i] > w)tp[++p]= sa[i] - w;//更新sa值,并用tp暂时存下上一轮的rk(用于cmp比较)RSort(), swap(rk, tp), rk[sa[1]]= p= 1;//用已经完成的sa来更新与它互逆的rk,并离散rkfor (i= 2; i <= n; i++)rk[sa[i]]= cmp(tp, sa[i], sa[i - 1], w) ? p : ++p;}//离散：把相等的字符串的rk设为相同。//LCPint j, k= 0;for (int i= 1; i <= n; height[rk[i++]]= k)for (k= k ? k - 1 : k, j= sa[rk[i] - 1]; a[i + k] == a[j + k]; ++k);//这个知道原理后就比较好理解程序
}
ll k;
ll sum[MAXN];
ll val[MAXN];
inline void clear()
{memset(tax, 0, sizeof(tax));memset(sa, 0, sizeof(int) * (n + 1));memset(height, 0, sizeof(int) * (n + 1));memset(rk, 0, sizeof(int) * (n + 1));memset(sum, 0, sizeof(int) * (n + 1));memset(tp, 0, sizeof(int) * (n + 1));memset(a, 0, sizeof(int) * (n + 1));
}void Init()
{scanf("%d%lld", &n, &k);scanf("%s", str + 1);for (int i= 1; i <= n; i++)a[i]= str[i];// cout << (str + 1) << endl;for (int i= 1; i <= 26; i++)read(val[i]);for (int i= 1; i <= n; i++)sum[i]= sum[i - 1] + val[str[i] - 'a' + 1];
}
bool check(int x)
{ll ans= 0;for (int i= 1; i <= n; i++) {int l= sa[i], r= n;while (l < r) {int mid= (l + r + 1) >> 1;if (sum[mid] - sum[sa[i] - 1] <= x)l= mid;elser= mid - 1;}if (sum[l] - sum[sa[i] - 1] <= x) {ans+= l - sa[i] + 1;ans-= min(height[i], l - sa[i] + 1);}}return ans >= k;
}
int main()
{//rd_test();int t;read(t);while (t--) {clear();Init();Suffix();int l= 1, r= 0;for (int i= 1; i <= n; i++)r+= val[str[i] - 'a' + 1];// cout << "r=" << r << endl;while (l < r) {int mid= (l + r) >> 1;if (check(mid))r= mid;elsel= mid + 1;}if (!check(l))l= -1;printf("%d\n", l);}//Time_test();
}