传送门

题意：

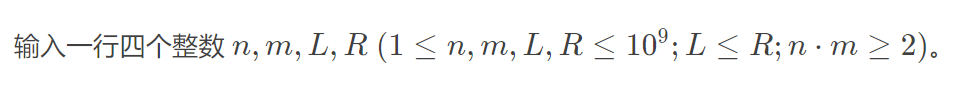
思路：

由于$n,m$都很大，不难猜到这是一个公式题。
首先化简题目中的两个操作，第二个操作就是可以让奇偶性相同的位置的高度相同。第一个操作虽然是改变相邻两个的奇偶性，但是仔细分析一下是可以改变任意两个位置的奇偶性，这里不多加证明，所以现在问题就变成了选$n\ast m$个数，只考虑选的奇偶性。
考虑当$n\ast m$为奇数的时候，那么选出来的数一定有偶数个奇数或者偶数个偶数，我们都可以用操作$1$将其转换成全部奇偶性都相同的，所以每个位置选的数任意，答案为$(r-l+1{)}^{n\ast m}$。
当$n\ast m$为偶数的时候，由于我们要将其转换成奇偶性相同的数，那么选出来的奇数和偶数的个数一定都是偶数，假设选了$x$个偶数和$y$奇数，答案为${\sum }_{k=0,2,4,..,2n}{\mathrm{C}}_{nm}^k{x}^k{y}^{nm-k}$ ，我们发现其就是$(x+y{)}^{nm}$的二项式定理的偶数项，所以答案为$\frac{(x+y{)}^{nm}-(x-y{)}^{nm}}{2}$。
用快速幂算一下就好啦。

// Problem: E. Height All the Same
// Contest: Codeforces - Codeforces Round #630 (Div. 2)
// URL: https://codeforces.com/contest/1332/problem/E
// Memory Limit: 512 MB
// Time Limit: 2000 ms
// 
// Powered by CP Editor (https://cpeditor.org)//#pragma GCC optimize("Ofast,no-stack-protector,unroll-loops,fast-math")
//#pragma GCC target("sse,sse2,sse3,ssse3,sse4.1,sse4.2,avx,avx2,popcnt,tune=native")
//#pragma GCC optimize(2)
#include<cstdio>
#include<iostream>
#include<string>
#include<cstring>
#include<map>
#include<cmath>
#include<cctype>
#include<vector>
#include<set>
#include<queue>
#include<algorithm>
#include<sstream>
#include<ctime>
#include<cstdlib>
#define X first
#define Y second
#define L (u<<1)
#define R (u<<1|1)
#define pb push_back
#define mk make_pair
#define Mid (tr[u].l+tr[u].r>>1)
#define Len(u) (tr[u].r-tr[u].l+1)
#define random(a,b) ((a)+rand()%((b)-(a)+1))
#define db puts("---")
using namespace std;//void rd_cre() { freopen("d://dp//data.txt","w",stdout); srand(time(NULL)); }
//void rd_ac() { freopen("d://dp//data.txt","r",stdin); freopen("d://dp//AC.txt","w",stdout); }
//void rd_wa() { freopen("d://dp//data.txt","r",stdin); freopen("d://dp//WA.txt","w",stdout); }typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int,int> PII;const int N=1000010,mod=998244353,INF=0x3f3f3f3f;
const double eps=1e-6;LL n,m,l,r;LL qmi(LL a,LL b) {LL ans=1;a%=mod;while(b) {if(b&1) ans=ans*a%mod;a=a*a%mod;b>>=1; }return ans%mod;
}int main()
{
//	ios::sync_with_stdio(false);
//	cin.tie(0);cin>>n>>m>>l>>r;if(n*m%2==1) printf("%lld\n",qmi(r-l+1,n*m));else {LL a=qmi(r-l+1,n*m);LL b=(r-l+1)%2;a+=b; a%=mod;a*=qmi(2,mod-2); a%=mod;printf("%lld\n",a);}return 0;
}
/**/