小白开学Asp.Net Core 《六》 —— 探究.Net Core 跨平台的奥秘

1、写这篇文章的初衷

　　有好多朋友反馈看不懂我写的开源的一个练手项目（GitHub：https://github.com/AjuPrince/Aju.Carefree）也有好多人都希望我能写一些简单的入门的文章，记得前几天在群里有人问为什么 .Net Core 能跨平台，在聊天中发现也有好多人在已经在使用 .Net Core ，但问他们的时候他们也表示不知道，还有好多人说既然 .Net Core 能跨平台了为啥还在Window上需要IIS来部署呢？因此我想通过这篇文章来试着解释下。（废话不多说，下面进入正题。）

2、概述

　　在Asp.Net Core 之前，Asp.Net Framework 应用程序由IIS加载，Web应用程序的入口由InetMgr.exe创建并调用托管，在初始化过程中触发HttpApplication.Application_Start()事件，我们第一次执行代码的机会是处理Application_StartGlobal.asax中的事件，但在Asp.Net Core中，Global.asax文件找不见了，被新的初始化过程所替换（回到了熟悉的控制台应用程序）

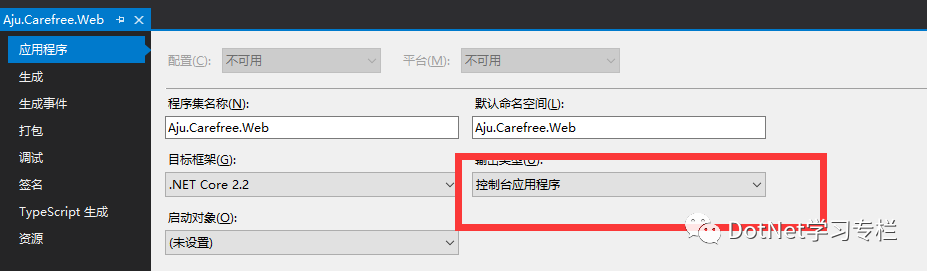
　　 640?wx_fmt=png

　　看上图的我圈住的地方，证明我没有吹牛皮。那就有好多人问了，既然是控制台应用程序，那为啥我没找见.exe 程序呢？

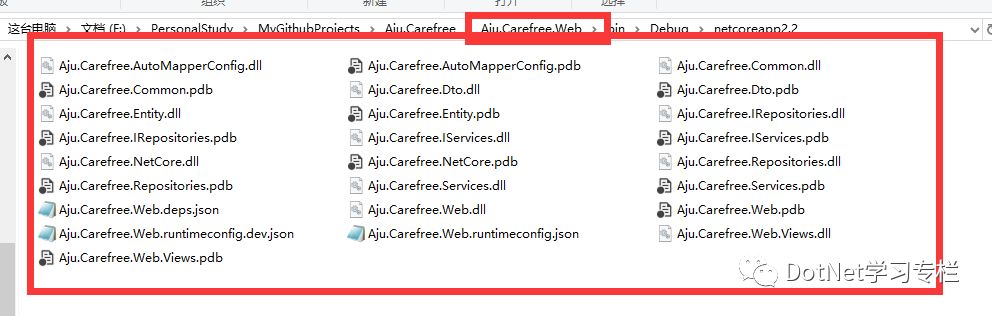
　　 640?wx_fmt=png

　　以图来说明，好像正的没有。很肯定的说是真的没有。这是为什么呢？（容我慢慢道来）

3、Program.cs

public class Program	{	public static void Main(string[] args)	{	CreateWebHostBuilder(args).Build().Run();	}	public static IWebHostBuilder CreateWebHostBuilder(string[] args) =>	WebHost.CreateDefaultBuilder(args)	.UseStartup<Startup>();	}

既然通过上面我们知道了.Net Core 应用程序是控制台应用程序，那么我们就很熟悉了，代码启动后肯定会找Main()函数（方法）（其实这就是ASP.NET Core应用程序开发的根本变化），所有的ASP.NET托管库都是从Program开始执行。

　　下面我们来解析下Main->CreateWebHostBuilder()方法

　　1、那先来看看CreateDefaultBuilder 方法　　

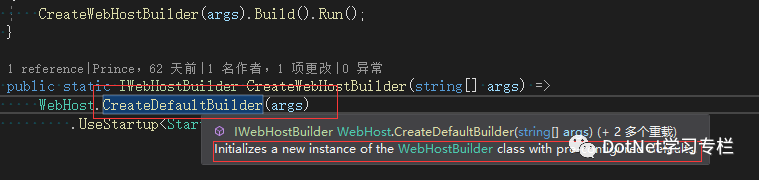
640?wx_fmt=png

从图中圈出来的注释来看，其实已经说的很明白了，我将试着解释下：使用预先配置的缺省值初始化WebHostBuilder类的新实例。（建议大家去看源码）搞懂这个东西就会理解 .Net Core 跨平台的秘密了，我简单的说下（算是给大家起个头，后面希望大家都去看看源码（.Net Core 是开源的，在GitHub上能找到）），这里方法里其实初始化了一个Kestrel Web服务器（至于什么是Kestrel 服务器后面有机会再介绍），在这个方法里默认使用系统配置文件 appsettings.json （注意，熟悉Asp.Net 的朋友们都知道有个Web.Config 配置文件，不好意思的说，在 .Net Core 中去掉了）等等。我觉得最主要的就是这两个。

　　可以这么说是有了Kestrel Web服务器才使得.Net Core 能真正的跨平台。

从上图的代码中可以看到，初始化完了系统默认的配置之后，启动了Startup类，那么下面我们就来看看这类

4、Startup 类　

public class Startup	{	public Startup(IConfiguration configuration)	{	Configuration = configuration;	}	public IConfiguration Configuration { get; }	// This method gets called by the runtime. Use this method to add services to the container.	public void ConfigureServices(IServiceCollection services)	{	services.Configure<CookiePolicyOptions>(options =>	{	// This lambda determines whether user consent for non-essential cookies is needed for a given request.	options.CheckConsentNeeded = context => true;	options.MinimumSameSitePolicy = SameSiteMode.None;	});	services.AddMvc().SetCompatibilityVersion(CompatibilityVersion.Version_2_2);	}	// This method gets called by the runtime. Use this method to configure the HTTP request pipeline.	public void Configure(IApplicationBuilder app, IHostingEnvironment env)	{	if (env.IsDevelopment())	{	app.UseDeveloperExceptionPage();	}	else	{	app.UseExceptionHandler("/Error");	// The default HSTS value is 30 days. You may want to change this for production scenarios, see https://aka.ms/aspnetcore-hsts.	app.UseHsts();	}	app.UseHttpsRedirection();	app.UseStaticFiles();	app.UseCookiePolicy();	app.UseMvc();	}	}

这是一个干净的（新建的Web程序）

　　从头来看，我们发现了一个很熟悉的方法——>构造函数，再仔细一看（原来是构造函数注入，这里就不在说IOC了，默认大家都知道。）

　接下来看看ConfigureServices和Configure 这两个方法

　　1、ConfigureServices

　 640?wx_fmt=png

　　通过注释可以得到（此方法由运行时调用。使用此方法向容器添加服务。）而且可以看到这个方法0个引用，更加的说明一点注释是不会骗人的。

　　这个方法的作用就是向IServiceCollection 这个集合里添加服务，也就是说以后系统中想要什么服务（比如MVC、Session、Cookie。。。）都添加到这个集合中。在F12看看IServiceCollection这个集合

　　 640?wx_fmt=png

　　可以看到这个集合的命名空间，可以说明一点（DI在.NET Core里面被提到了一个非常重要的位置）

2、Configure 方法

　　 640?wx_fmt=png

　　通过注释（此方法由运行时调用。使用此方法配置HTTP请求管道。）可以了解到这个异常之重要，此方法用于指定中间件以什么样的形式响应HTTP请求，网上文章都说的亲求处理管道（中间件）就是在这个方法里配置的。

5、总结

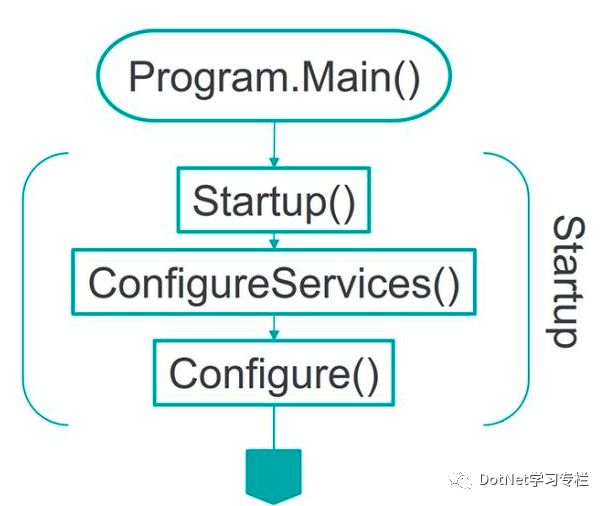
　 640?wx_fmt=png

　　借用网上的一张图来总结。

ASP.NET Core在运行时首先加载Program类下面的Main方法，在Main方法中指定托管服务器，并调用Startup类中的Configure和ConfigureServices方法等完成初始化
在ASP.NET Core中 HTTP请求是以中间件管道的形式进行处理
.Net Core 应用程序不需要用IIS进行托管，所以相比传统Asp.Net来说性能更高效也更加灵活
.Net Core 跨平台在于维护了自己的内部Web服务器（Kestrel ）

　本篇文章只为了让大家入门，更深入的东西后面有时间再深入，如有不合适的地方请反馈，本人将马上修改！

　　如果觉得还不错，还请大家点个推荐（哈哈）！