10分钟了解分布式CAP、BASE理论

CAP理论

2000年7月，Eric Brewer教授提出CAP猜想；2年后，Seth Gilbert和Nancy Lynch从理论上证明了CAP；之后，CAP理论正式成为分布式计算领域的公认定理。CAP定律说的是在一个分布式计算机系统中，一致性，可用性和分区容错性这三种保证无法同时得到满足，最多满足两个。CAP：C ：Consistency（一致性）A：（Availability）可用性P：（Partition Tolerance）分区容错性

让我们构造一个非常简单的分布式系统。

两台服务器G1和G2
两台服务器可以相互通讯
客户端可以随机访问任何一台服务器

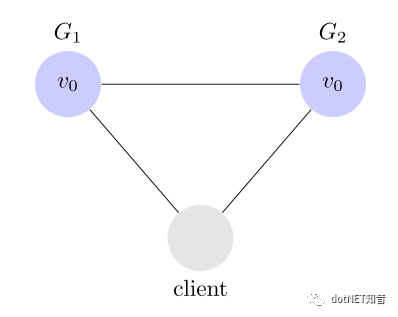
640?wx_fmt=png

Consistency（一致性）

Gilbert and Lynch 这样描述的一致性.

any read operation that begins after a write operation completes must return that value, or the result of a later write operation

在写操作完成之后的任何读操作都必须返回该值。

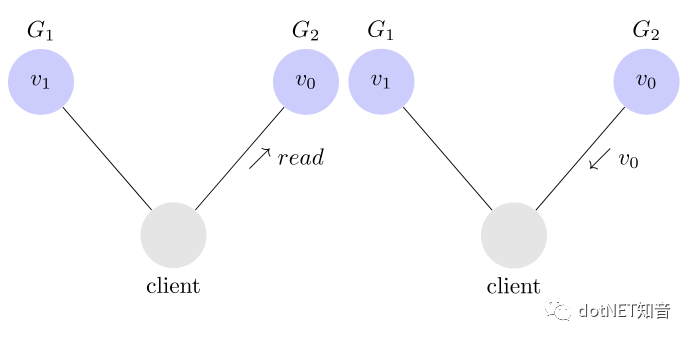
客户端向G1服务器发起一个写操作，把变量初始值v0 改为v1，接下来客户端可能向节点G1读取也可能向节点G2读取;

向G1发起一个读操作，得到更改后的值V1。这就是满足了一致性

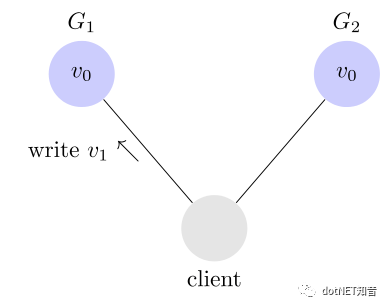
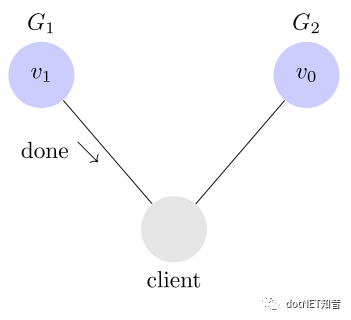
640?wx_fmt=png

向G2发起一个读操作，此时G1向G2发送同步消息

如果同步完成，那么读到的结果是v1，这样也满足了一致性

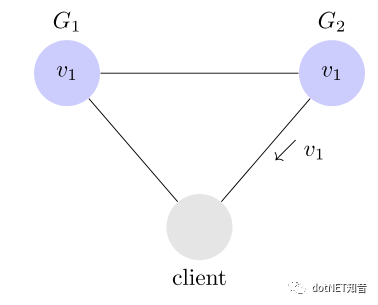
640?wx_fmt=png

还未同步完成，这是G2还是v0，这就不满足一致性。

640?wx_fmt=png

（Partition Tolerance）分区容错

Gilbert and Lynch 这样描述的分区容错.

the network will be allowed to lose arbitrarily many messages sent from one node to another

网络允许丢失任意多的消息从一个节点发送到另外一个节点

在分布式环境中，节点之间的通信可能出现问题，整个系统就产生所谓的分区。所以我们在设计的时候需要考虑这种情况；剩下来的 A和C满足好，我们就可以说我们的系统有很好的分区容错性。

（Availability）可用性

Gilbert and Lynch 对 availability的描述原文. every request received by a non-failing node in the system must result in a response 系统中非失败节点收到的每个请求都必须导致响应在可用性系统中，只要服务器没有奔溃，客户端发送请求，服务器必须返回一个相应给客户端。

为什么要CAP不能同时满足

通过上述的定义和描述知道分区无法避免，p总是要考虑的。为什么c和a无法同时做到呢？其实都是分区惹的祸。

如果我们保证一致性；那么G1写入操作之后，必须保证数据同步给G2之后，G2才能对外提供响应，这显然就没有可用性了。

反之我们保证可用性，那就没法保证一致性了，既生瑜何生亮的悲剧。

小结

经过上面分析，在分布式系统中，我们一般会选择AP而牺牲一致性。牺牲并不意味着不关心一致性，而是首先满足A和P，如何解决C的问题。参考以下BASE理论

BASE 理论

eBay的架构师Dan Pritchett源于对大规模分布式系统的实践总结，在ACM上发表文章提出BASE理论，BASE理论是对CAP理论的延伸，核心思想是即使无法做到强一致性（StrongConsistency，CAP的一致性就是强一致性），但应用可以采用适合的方式达到最终一致性（Eventual Consitency）。