最近几年微服务很火，大家都在建设微服务，仿佛不谈点微服务相关的技术，都显得不是那么主流了。
近几年见识到身边朋友的很多公司和团队都在尝试进行微服务的改变，但很多团队并没有实际微服务踩坑经验，很多团队甚至强行为了微服务而去微服务，最终写成一个大型的分布式单体应用，就是改造后的系统既没有微服务的快速扩容，灵活发布的特性，也让原本的单体应用失去了方便开发，部署容易的特性（项目拆为多份，开发部署复杂度都提高了），不得不说是得不偿失。
作者亲身经历和参与几个大型项目微服务的改造和建设。所以想作为实践者跟大家分享关于微服务的实际经验，帮助大家了解微服务的优缺点，从而可以结合自身业务做出更加合适的选择，作为本篇文章的三个主题，例如：
什么是微服务？为什么要用微服务？
微服务解决什么问题，又引入了什么问题？
使用微服务应该要遵循哪些原则？什么样的情况你不应该使用微服务？
（PS：因为市面上太多对如果使用微服务框架工具的教程，所以本篇只是一篇关于微服务的总体概述性文章，不涉及各种微服务框架的安装和使用教程，我们只谈论微服务本身的设计模式的优缺点和适合应用的场景）
一：什么是微服务？为什么要用微服务？
什么是微服务？（熟悉的同学可以直接跳过）
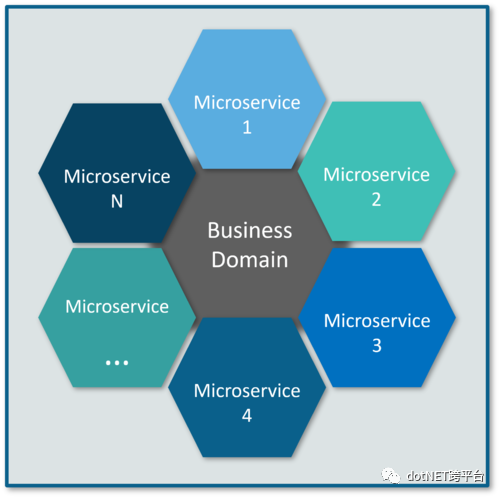
简单举例：看军事新闻的同学应该都知道，一艘航空母舰作战能力虽然很强，但是弱点太明显，就是防御能力太差，单艘的航空母舰很少单独行动，通常航空母舰战斗群才是主要军事力量，你可以把单艘航母理解为的单体应用（防御差，机动性不好），把航母战斗群（调度复杂，维护费用高）理解为微服务。
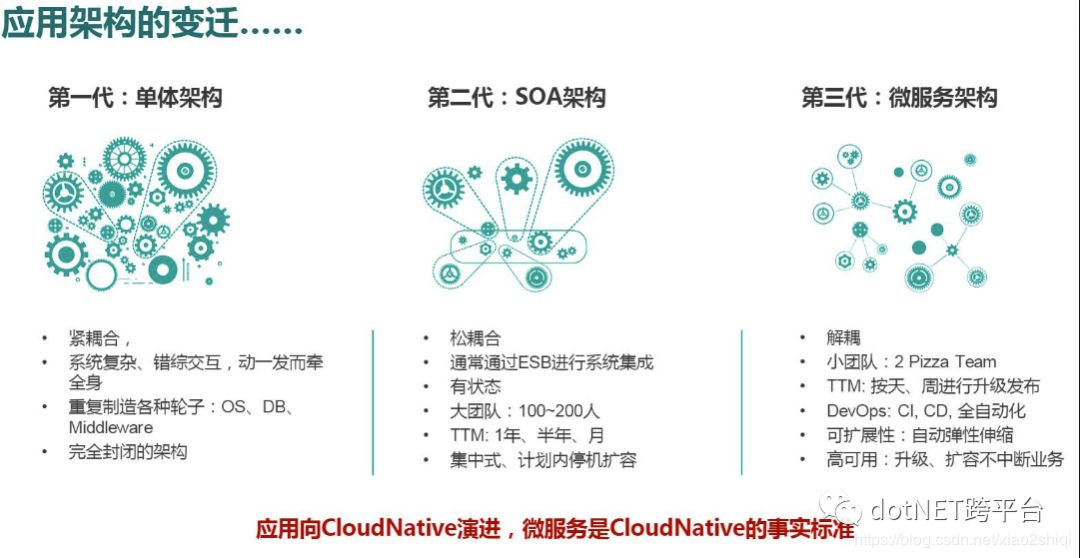
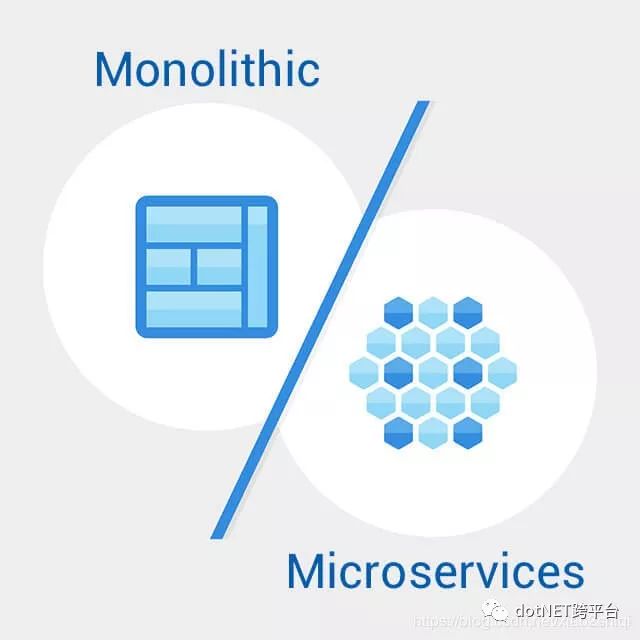
大部分的开发者经历和开发过单体应用，无论是传统的 Servlet + JSP，还是 SSM，还是现在的 SpringBoot，它们都是单体应用，那么长期陪伴我们的单体应用有什么弊端？我们是面临了什么问题，导致我们要抛弃单体应用转向微服务架构？个人总结主要问题如下：
部署成本高（无论是修改1行代码，还是10行代码，都要全量替换）
改动影响大，风险高（不论代码改动多小，成本都相同）
因为成本高，风险高，所以导致部署频率低（无法快速交付客户需求）
当然还有例如无法满足快速扩容，弹性伸缩，无法适应云环境特性等问题，但我们不一一详谈了，以上的问题，都是微服务架构要解决的问题，至于具体是怎么解决的，我们先放到后面再聊
二：微服务解决什么问题，又引入了什么问题？
我们先看看微服务能带给我们什么？微服务架构的特点：
针对特定服务发布，影响小，风险小，成本低
频繁发布版本，快速交付需求
低成本扩容，弹性伸缩，适应云环境
我们知道一个朴素的理念，没有任何事物是完美的，任何东西都有两面性，有得必有失，那么在选择微服务在解决了快速响应和弹性伸缩的问题同时，它又给我们带来了什么问题？个人总结如下：
分布式系统的复杂性
部署，测试和监控的成本问题
分布式事务和CAP的相关问题
系统应用由原来的单体变成几十到几百个不同的工程，会所产生例如包括服务间的依赖，服务如何拆封，内部接口规范，数据传递等等问题，尤其是服务拆分，需要团队熟悉业务流程，懂得取舍，要保证拆分的粒度服务既符合“高内聚，低耦合”的基本原则，还要兼顾业务的发展以及公司的愿景，要还要说服团队成员为之努力，并且积极投入，在多方中间取得平衡。
对于分布式系统，部署，测试和监控都需要大量的中间件来支撑，而且中间件本身也要维护，原先单体应用很简单的事务问题 ，转到分布式环境就变得很复杂，分布式事务是采用简单的重试+补偿机制，还是采用二阶段提交协议等强一致性方法来解决，就要取决对业务场景的熟悉加上反复的权衡了，相同问题还包括对 CAP 模型的权衡，总之微服务对团队整体的技术栈水平整体要求更高
三：使用微服务应该遵循哪些原则？
古人云：兵马未动，粮草先行。建设微服务是需要建立长远规划，不是像写CMS那样建好数据库表，然后就开始干活，这样十有八九是会失败的。我们要进行微服务改造前，架构师要提前做好规划，我们把这里分为三步，前期阶段，设计阶段，技术阶段
前期阶段，大致要做好如下事情：
和多方充分沟通，确保能符合客户和组织的需求，并且得到认同
和团队沟通，让队友（开发/测试/运维）理解，并且积极投入
和业务部门沟通，指定版本计划和上线时间
设计阶段，参考 Sam Newman 的著作《微服务设计》，单微服务必须要满足以下的条件，才符合微服务的基本要求：
标准的 REST 风格接口（基于 HTTP 和 JSON 格式）
独立部署，避免共享数据库（避免因为数据库而影响整个分布式系统）
业务上的高内聚，减少依赖（从设计上要避免服务过大或者太小）
庞大的分布式系统，需要强大基础设施来支撑，微服务涉及哪些基础设施？
CI/CD和自动化（分布式系统几乎不可能通过人工手动发布）
虚拟化技术（要保证微服务运行环境隔离，目前行业主流的是使用 Docker 容器）
日志聚合，全链路监控（高度可观察和分析诊断问题）
说了那么多，那什么样的情况下，你的团队不适合建设微服务？（请勿对号入座）
开发团队不具备自主性，所在组织对开发团队限制非常多（具体请参考 康威定律）
团队不熟悉业务，无法识别出服务的边界，进行合理的拆分（请参考 DDD 领域驱动设计）
总结
微服务设计其实是很早就有的设计思想，因为随着虚拟化技术的崛起，微服务可以低成本的实现，所以也开始流行和兴起。
微服务的内涵很深，其中就包括，自动化，去中心化，独立性等等，其中细节无法用一篇文章概述清楚，我们在做技术选型或者方案的时候，尽可能多去了解技术的本身和起源再结合我们业务的特点，进行更好的选择。
个人知识有限，不喜勿喷，对于微服务你又有什么不同的看法呢？欢迎来留言进行讨论和交流
原文链接：https://www.cnblogs.com/xiao2shiqi/p/11298663.html
.NET社区新闻，深度好文，欢迎访问公众号文章汇总 http://www.csharpkit.com
