引言：

作为资深老鸟，有事没事，出去面试；找准差距、定位价值。

面试必谈哈希，

Q1：什么是哈希?

Q2：哈希为什么快?

Q3：你是怎么理解哈希算法利用空间换取时间的？

Q4：你是怎么解决哈希冲突的？

Q5：你有实际用写过哈希算法吗？

1. 知识储备

　　哈希（也叫散列）是一种查找算法（可用于插入），哈希算法希望能做到不经过任何比较（发生冲突，还是需要少许比较），通过一次存取就能得到查找的数据。

因此哈希的关键在key和数据元素的存储位置之间建立一个确定的对应关系，每个key在哈希表中都有唯一的地址相对应（形成有限、连续的地址空间），查找时根据对应关系经过一步计算得到key在散列表的位置。

在数学上， 原Key叫做原像，由映射函数h(key)映射的存储位置叫做像；在IT领域，以上存储位置叫哈希地址（散列地址），这个映射过程叫做哈希/散列。

故我们可以预见：

　　① 不同的key值，由哈希函数h(x) 作用后可能映射到同一个哈希地址， 这就是哈希冲突，冲突发生的概率取决于 定义的哈希函数

　　② 由哈希表作用后的哈希地址需要空间存储，这一系列连续相邻的地址空间叫哈希表、 散列表。 

　　处理哈希冲突可分为两大类：

　　（1）开散列法发生冲突的元素存储于数组空间之外。可以把“开”字理解为需要另外“开辟”空间存储发生冲突的元素， 又称【链地址法】

　　（2）闭散列法发生冲突的元素存储于数组空间之内。可以把“闭”字理解为所有元素，不管是否有冲突，都“关闭”于数组之中，闭散列法又称【开放定址法】，意指数组空间对所有元素，不管是否冲突都是开放的

 　　哈希表是用数组实现的一片连续的地址空间，两种冲突解决方案的区别在于发生冲突的元素是存储在这片数组的空间之外还是空间之内

2. 看图说话

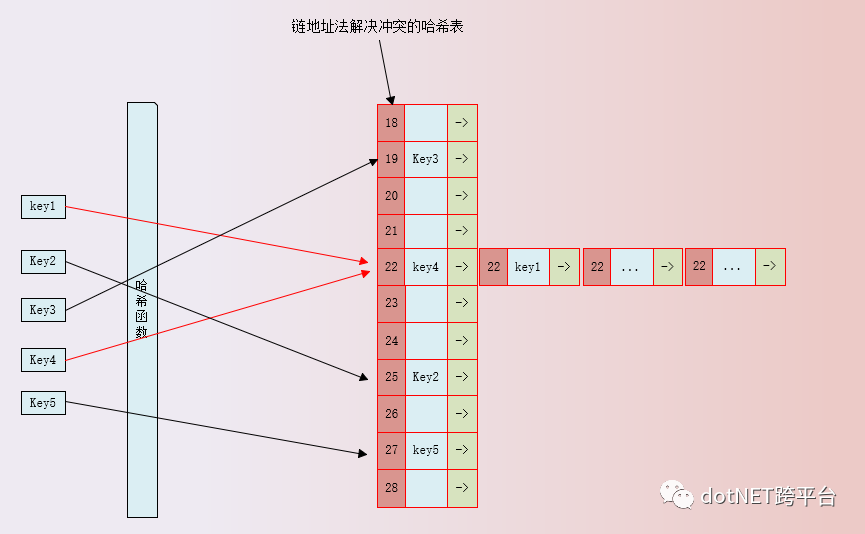
---以下是开散列法（链地址法）解决冲突的示意图------

　　从图上看实现【哈希】过程分两部分：

① 哈希函数

　　收敛函数，不可避免会冲突，需要思考设定一个均衡的哈希函数，使哈希地址尽可能均匀地分布在哈希地址空间

②  构造哈希表 + 冲突链表

　　装填因子loadfactor ：所谓装填因子是指哈希表中已存入的记录数n与哈希地址空间大小m的比值，即 α=n / m ，α越小，冲突发生的可能性就越小；α越大（最大可取1），冲突发生的可能性就越大。

　　另一方面，α越小，存储窨的利用率就越低；反之，存储窨的利用率就越高。为了既兼顾减少冲突的发生，又兼顾提高存储空间的利用率，通常把α控制在0.6～0.9的范围之内

哈希在.Net中的应用

　　Object基类中有GetHashCode方法，HashCode是一个数字值，用于在【基于哈希特性的集合】中插入和查找某对象；GetHashCode方法为需要快速检查对象相等性的算法提供此哈希代码；

　　Do not test for equality of hash codes to determine whether two objects are equal. (Unequal objects can have identical hash codes.) To test for equality, call the ReferenceEquals or Equals method.  （重要的话要读3遍）

单纯判断【逻辑相等】时，本无所谓重写 GetHashCode方法；但若在基于hash的集合中快速查找/插入某元素，则一定要重写GetHashCode方法。

? 我们看一个实锤：

　　统计参加Footabll,Basketball 两个球队的所有成员，自然会想到对 footabllTeam, basketballTeam 成员使用Union方法求并集 （A∪B）

　　观察Union源码计算A,B并集的实现，内部会构造哈希表Set<TElement> 快速查找和插入并集元素，故我们需要给元素编写合适的哈希函数。

public static IEnumerable<TSource> Union<TSource>(this IEnumerable<TSource> first, IEnumerable<TSource> second, IEqualityComparer<TSource> comparer)

{

    if (first == null) throw Error.ArgumentNull("first");

    if (second == null) throw Error.ArgumentNull("second");

        return UnionIterator<TSource>(first, second, comparer);

}

static IEnumerable<TSource> UnionIterator<TSource>(IEnumerable<TSource> first, IEnumerable<TSource> second, IEqualityComparer<TSource> comparer)

{

      Set<TSource> set = new Set<TSource>(comparer);

      foreach (TSource element in first)

          if (set.Add(element)) yield return element;      //  Set 便是Union方法内部构造的哈希表

      foreach (TSource element in second)

           if (set.Add(element)) yield return element;

}

Union方法入口

 

高潮来了，不是总说没处理过哈希冲突吗？结

合

【知识储备】

围观链地址法处理哈希冲突：

因此有最佳实践: 当两对象重写Equal方法返回true时， 请务必重写GetHashCode方法为对象返回相同的hashcode。

话虽如此，写一个合适、均衡的哈希函数还是比较考验算法的。

在一般场景中，经验会帮助你编写哈希函数， 比如以上Person类中，字符串类型Name的HashCode总是相等的。

That‘all   看完了通篇文章的同栈猿，应该就可以回答文章引言 5大提问。