工作中我们经常会遇到一些一些功能需要实现造作日志，数据修改日志，对于这种业务需求如果我们以同步的方式实现，难免会影响到系统的性能。如下我列出集中解决方案。

• 使用Thread异步处理。

• 使用线程池或Task异步处理。

以上两种方案确实能解决我们此场景的需求，但是同时也带来了问题。

第一种方式，使用thread的情况下我们无法控制创建的线程数量，要知道创建线程是一个很耗性能的操作。

第二种方式，使用线程池或者Task我们虽然可以通过设置线程池的最大线程数量来限制线程最大数，但是这个设置由于是全局的，就会造成所有使用线程池或Task的地方都会受到此设置的限制。

当然，第二种方式肯定是优于第一种方式的，我们都是有追求的程序员，做事情当然是追求精益求精。基于此思想的驱动我实现了一个轻量级的多线程队列。她有如下特点：

• 可以设置线程数量，空闲睡眠次数，空闲睡眠时间。空闲睡眠次数和空闲睡眠时间共同控制线程的销毁。

• 可以设置任务的优先级，提供三种优先级：LOWEST，NORMAL，HIGHEST。

• 可以设置多线程的模式是使用Thread还是使用Task.

• 可以提高任务的优先级。

当然首先要说的是使用方法，当我设置使用一个线程的时候如下代码：

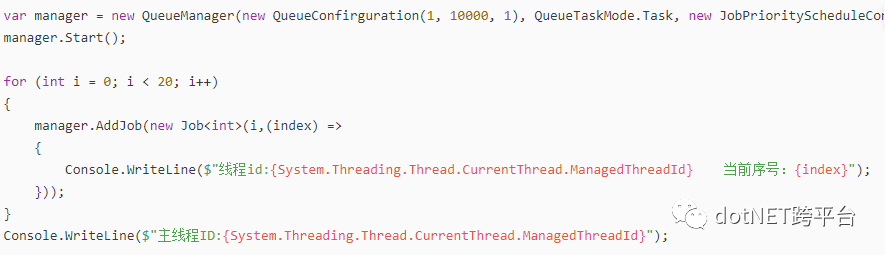
输出结果如下

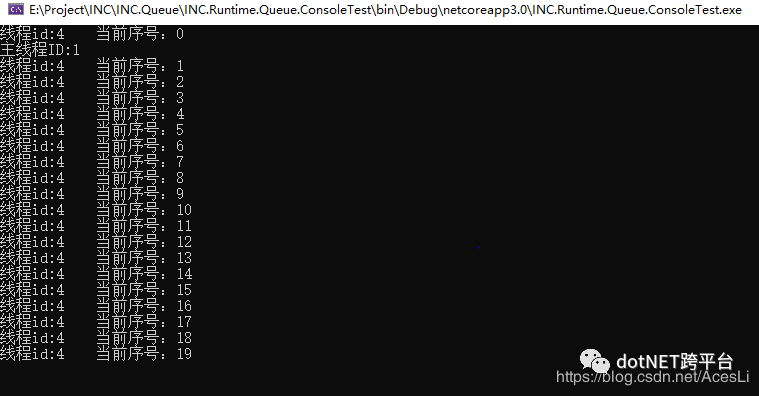
可以看到使用QueueManager类的线程都是id=4的线程上执行，这是由于我们设置的是一个线程，主线程的id为1，并且可以看到Job中的代码是异步执行的。当我们将线程数设置成2的时候输出如下

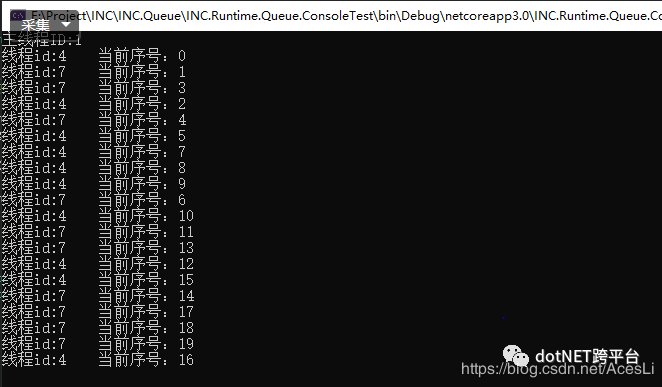
使用其它是不是很简单？？

那么我分别来讲一下QueueManager类的参数

1. QueueConfirguration类，结构如下。

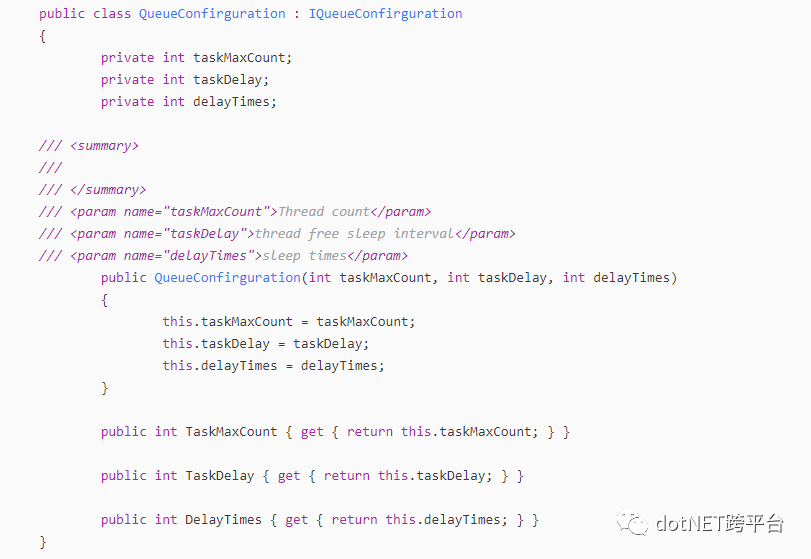
TaskMaxCount：线程数量，TaskDelay：为空闲时线程睡眠时间（ms单位），delayTimes：睡眠次数

2. QueueTaskMode:枚举类型，提供两种多线程使用方式Thread和Task

3.JobPriorityScheduleConfig:实现接口IJobPriorityScheduleConfig，用来提升Job的优先级。

各位朋友可能也看到了我使用了一个Job类，目前总共有三种Job类型

• Job：无参数无返回

• Job<T>：有参数无返回

• Job<T1, T2> ：有参数有返回， 同时提供执行完成之后返回参数的callback事件。

当然，代码中还有很多地方可以优化，譬如：

1. 当线程处于睡眠中时，有Job需要执行时的interrupt.

2. AddJob方法可以加一些重载。

3. 实现中的事件可以修改为委托，以达到减少一些委托类型的定义。

具体代码可以访问我的github仓储：https://github.com/Roger3Lee/INC.Runtime.Queue 查看。如果喜欢还请Star一下,当然也希望各位同仁能提供意见，谢谢。

原文链接：https://blog.csdn.net/AcesLi/article/details/98998592

---

.NET社区新闻，深度好文，欢迎访问公众号文章汇总 http://www.csharpkit.com