前言：本系列博客又更新了，是博主研究很长时间，亲自动手实践过后的心得，k8s集群是购买了5台阿里云服务器部署的，这个集群差不多搞了一周时间，关于k8s的知识点，我也是刚入门，这方面的知识建议参考博客园大神edisonchou的系列文章《.NET Core on K8S学习实践系列文章索引(Draft版)》，为什么我要写该系列的文章，是因为我之前 工作的几家公司应用都已经容器化了，.net framework 应用也在慢慢迁移到.net core 上，.net core 从1.0就开始使用了，作为开发人员，有些细节上的东西对开发人员是封闭的，我们只知道项目开发完成通过Jenkins构建，构建完成把镜像推送到HarBor，然后在禅道上建个发布任务，贴上镜像的地址，发给运维就好了。我就对这个过程很好奇，业余时间也在研究这方面的东西。好了，暂且聊到这里，下面我就分享一下自己在搭建k8s集群的心得，有说的不对的地方还请纠正。

我们都知道Kubernetes自身，侧重稳定性、可扩展性、安全性；核心策略的变化小；周边生态持续爆发。k8s搭建的方式有三种：（1）社区方案：杂乱、不可靠、升级难（2）kubeadm：优雅、简单、支持高可用、升级方便、不易维护、文档不够细致 （3）二进制部署，建议初学者使用二进制搭建，因为可以快速放弃，哈哈哈，玩笑归玩笑，二进制的方式易于维护、灵活、升级方便。我的k8s集群使用的是二进制搭建的，5台阿里云的配置 如下：

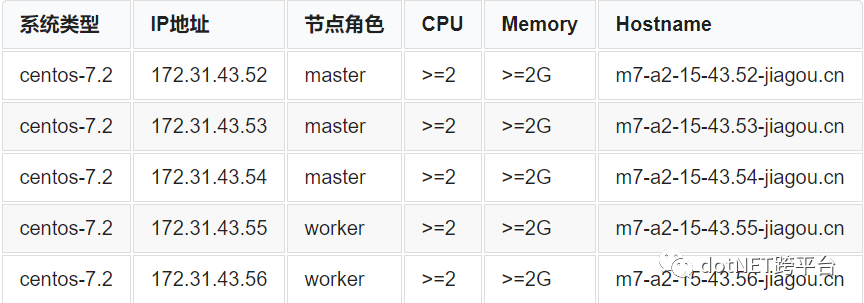
环境参数：k8s 1.14.0  Docker 17.03.1-ce  Harbor 1.6.0  Jenkins v2.150.2，一定 要注意版本问题，

注意：使用云服务器的，跳过keepalived的配置，不要用虚拟ip（云环境一般都不支持自己定义虚拟ip）就直接把虚拟ip设置为第一个master的ip就可以了。

 PS：如果是一定要高可用的话可以购买云商的负载均衡服务（比如阿里云的SLB），把backends设置成你的三个master节点，然后虚拟ip就配置成负载均衡的内网ip即可。

具体的集群搭建细节，我就不列出来了，因为不是重点。

• 准备Deployment YAML

这个YAML文件，引用自Edison Zhou（https://www.cnblogs.com/edisonchou/p/aspnet_core_on_k8s_firststudy_part3.html），在这里我们使用了Edison Zhou的镜像仓库 

apiVersion: apps/v1
kind: Deployment
metadata:
  name: k8s-demo
namespace: aspnetcore
  labels:
    name: k8s-demo
spec:
  replicas: 2
  selector:
    matchLabels:
      name: k8s-demo
  template:
    metadata:
      labels:
        name: k8s-demo
    spec:
      containers:
- name: k8s-demo
        image: edisonsaonian/k8s-demo
        ports:
- containerPort: 80
        imagePullPolicy: Always

---

kind: Service
apiVersion: v1
metadata:
  name: k8s-demo
namespace: aspnetcore
spec:
  type: NodePort
  ports:
- port: 80
      targetPort: 80
  selector:
    name: k8s-demo

这里这个deploy.yaml就会告诉K8S关于你的API的所有信息，以及通过什么样的方式暴露出来让外部访问。

　　需要注意的是，这里我们提前为要部署的ASP.NET Core WebAPI项目创建了一个namespace，叫做aspnetcore，因此这里写的namespace : aspnetcore。

　　K8S中通过标签来区分不同的服务，因此这里统一name写成了k8s-demo。

　　在多实例的配置上，通过replicas : 2这个设置告诉K8S给我启动2个实例起来，当然你可以写更大的一个数量值。

　　最后，在spec中告诉K8S我要通过NodePort的方式暴露出来公开访问，因此端口范围从上一篇可以知道，应该是 30000-32767这个范围之内。

• 通过kubectl 部署到k8s

需要先后执行以下命令：

kubectl create namespace aspnetcore // 创建一个命名空间“aspnetcore”

cd aspnetcore/
vim deploy.yaml  //将上面的配置写入该文件中
kubectl create -f deploy.yaml

[root@m7-a2-15-43 aspnetcore]# kubectl get svc -n aspnetcore
NAME       TYPE       CLUSTER-IP       EXTERNAL-IP   PORT(S)       AGE
k8s-demo   NodePort   10.254.180.117   <none>        80:8671/TCP   4h55m

可以看到在命名空间aspnetcore下，就有一个k8s-demo的服务运行起来了，并通过端口号8671向外提供访问。

• 验证WebAPI是否可以访问

首先，在浏览器中访问API接口，看看是否能正常访问：http://公网IP:8671/api/values

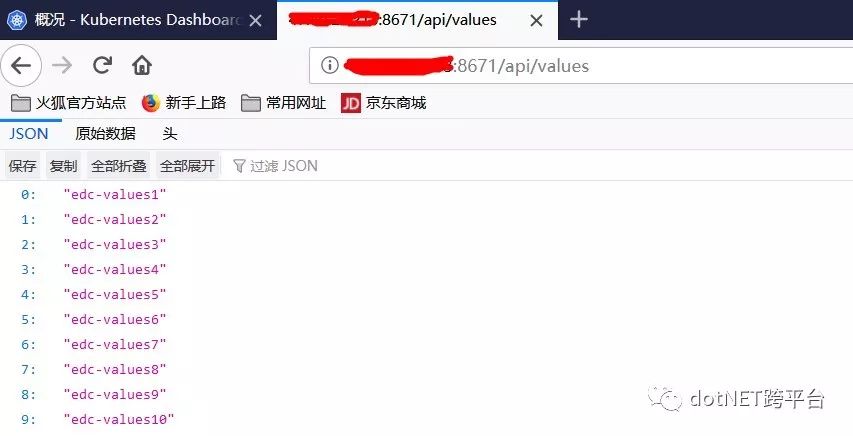
然后，我们再到Dashboard中，看看k8s-demo的状态：

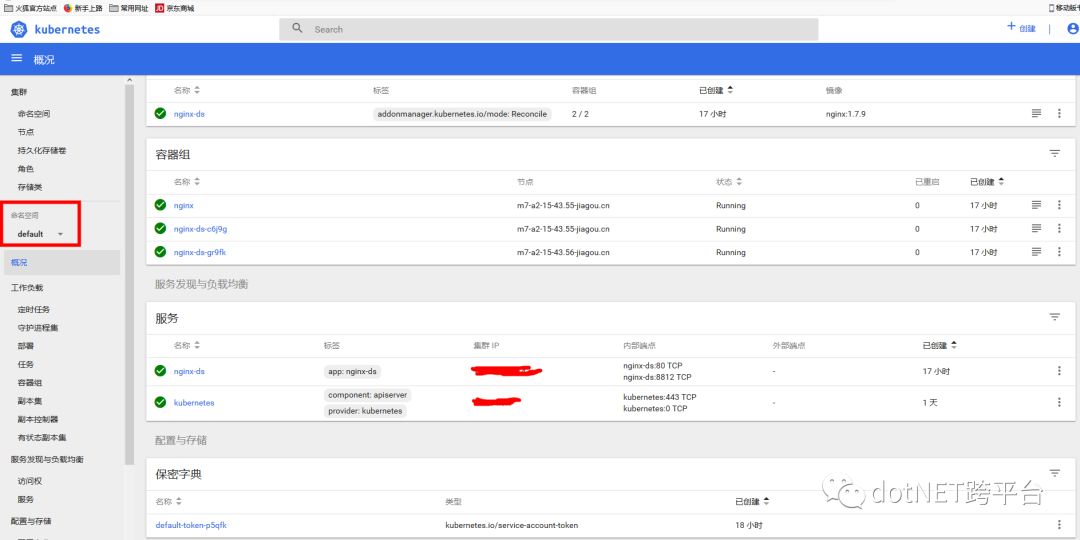
我们点击命名空间，选择：aspnetcore

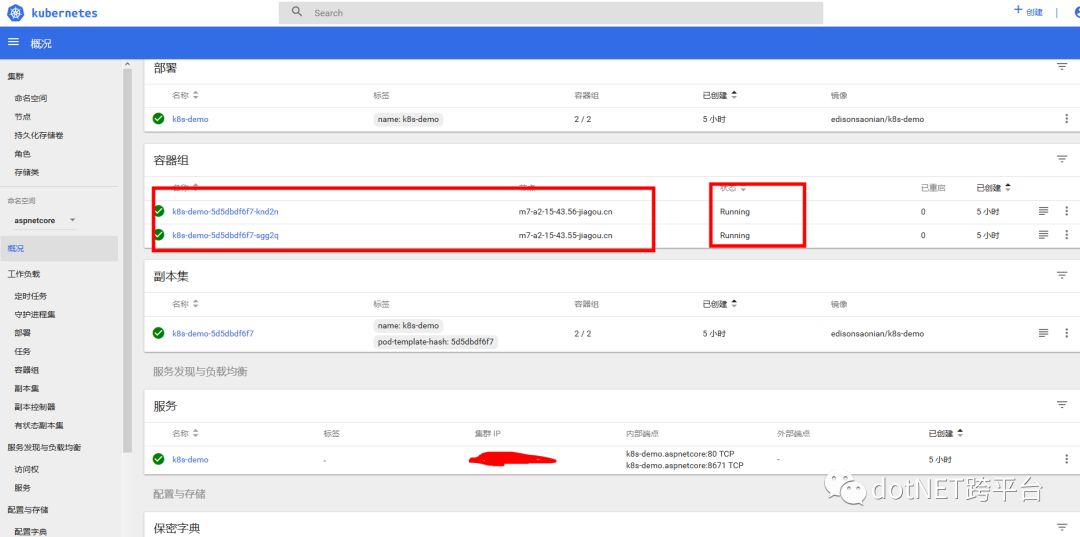
当然了，你也可以直接点击：“集群”选项下面的“命名空间”，点击对应的名称，里面可以看到详细的信息。从Dashboard中可以看到更为详细的信息，包括运行的Deployment、容器组（由于我们设置的replicas=2，因此会有2个容器运行起来）、副本集等等，也可以通过Dashboard实时初步地监控我们的API的运行情况。

• 通过Dashboard伸缩WebAPI

在Dashboard中，我们可以可视化地对我们的Deployment进行容器实例的伸缩，具体操作可以参考：https://www.cnblogs.com/edisonchou/p/aspnet_core_on_k8s_firststudy_part3.html，这里我就不再多说了。

本文，简单总结了一下使用阿里云部署高可用k8s集群，可能有同学说怎么不详细写一下部署的过程呢？由于时间仓促，部署的过程文档还在整理中，况且，部署的过程和该系列文章的主题不符，大家可以参考其他文章，关于Dashboard，一般企业内部是不会使用的，都是自研的，只需要了解即可。该篇文章的目的，是 想让大家体验一下所谓的容器编排，以及asp.net core on k8s。笔者也是刚接触，有很多东西需要学习，这只是k8s的一点点，因为还没用到生产 环境，需要观察一段时间，后期，我把部署的过程整理一下，再分享给大家。提前预告一下篇博客的主题：Jenkins+k8s，实现CI/CD，敬请期待。

这是该系类博客要使用的项目：https://github.com/guozheng007/asp.net-core2.1-miaosha-project

Edison Zhou：https://www.cnblogs.com/edisonchou/p/aspnet_core_on_k8s_firststudy_part3.html

刘果国：https://coding.imooc.com/class/335.html（付费课程366.00）

原文链接：https://www.cnblogs.com/runningsmallguo/p/11345620.html

---

.NET社区新闻，深度好文，欢迎访问公众号文章汇总 http://www.csharpkit.com