这里是Z哥的个人公众号

每周五11：45 按时送达

当然了，也会时不时加个餐～

我的第「86」篇原创敬上

俗话说的好，不以规矩，不成方圆。

但是有些时候，可能破坏规则反而是一个更有效的方式，这个时候到底该不该打破规则办事呢？

比如前几天发生在Z哥身边的一个例子。

公司有一个临时的事需要处理，针对其中的在系统上做单子该由那边进行产生了分歧。

这项工作呢，按照岗位职责来说是部门A来负责做，但是在这个临时的事情中，部门A觉得部门B直接来做的话，效率更高。

因为这个临时工作的主导方是部门B，并且在这件事中，部门A做单子的工作需要依赖部门B提供的数据进行，所以部门A索性建议部门B自己来做。（其实部门B对怎么做单子并不熟悉，但是这个比较容易学会）

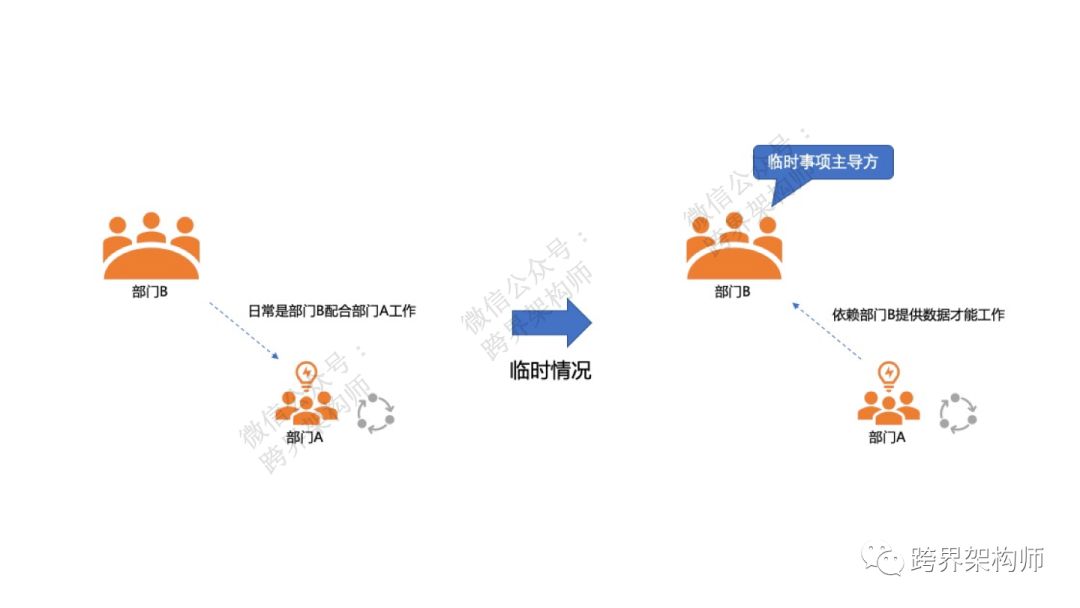
这就是一个典型的短期利益和原有规则冲突的例子。

到底该选择“短视”（非贬义）？还是坚守规则？可能没有统一的标准答案，但是该如何思考这个问题才比较合理，还是有深入挖掘的意义的。

为什么“短视”的决策更容易作出

上面的例子中，部门A给出的建议看上去是针对当下这个问题的最优解。哪怕真的是这样，本质上还是一个“短视”的决定，因为考虑的范围仅限于“当下”。

有一个实验揭示了「我们为什么更容易作出“短视”的决定」背后的一些奥秘。

2004年，普林斯顿大学做了一项研究，通过扫描人类大脑的方式观察面对短期利益和长期利益时，大脑的表现。

• 当实验对象接受即时奖励时，他们的大脑边缘区高亮，也就是这一区域产生了大量的神经活动。

• 当研究者向实验对象承诺未来给予他们某些奖励时，实验对象的大脑边缘完全不亮。进一步研究后发现是由大脑的前额叶皮质发动的。

是不是很有意思。

说明我们作出的决定是不是“短视”，并不是由一个中心节点控制的，而是分别由两个不同的节点控制的，哪一边胜出，决定了你的选择是“短视”还是“不短视”。

然而，大脑边缘系统的“辈分”可比前额叶老的多。

前者在原始社会就已存在，是“短视”、“冲动”的主人，它又被称作“蜥蜴脑”；而后者是相对现代的结构，负责抽象思维、解决复杂问题、保持理性。

所以，以后你有个理由可以说了，我“短视”也是不得已，生理反应：D

哈哈，开个玩笑：D。

其实从我们人类的进化过程来看，前额叶皮层的“壮大”就是我们有别于其它灵长类动物的地方。

之所以会这样，是因为「长期主义」正在逐渐主导着我们的思考方向，不断的刺激和训练前额叶皮层。

如果我们只是乐于追求短期的快感，那么其实和其它的动物无异，根本不会存在相互合作的可能性。因为，单是决定谁先迈出第一步，就足以让合作陷入僵局。

想改变自己短视的“生理反应”，让自己变得更加理性，培养「长期主义」思想，首先得对“短视”的副作用，有更深的认识。

短视的副作用

首先，大多数情况下，短期利益与长期利益是冲突的。所以，“短视”会损害长期的利益。

这一点是广为人知的。

有多少企业因为选择了赚快钱而透支未来，导致陷入困境。

有多少人又因为选择了高薪，而做着自己并不擅长，或者并不敢兴趣的工作，导致未来的职业道路越走越窄，落得一个焦虑的中年期。

其次，原先的规则起到平衡作用被打破。这必然导致了打破规则后，有人获益，有的人则利益受损。

大家都遵守规则在排队，一个人来插队，这个人自身是赚了，但是其它的利益则受损害了。

最后，更严重的是，“短视”行为会引导更多人一起选择“短视”。心理学中的「破窗效应」很好阐述了这个后果。

以一幢有少许破窗的建筑为例，如果那些窗没修理好，可能将会有破坏者破坏更多的窗户。最终他们甚至会闯入建筑内，如果发现无人居住，也许就在那里占领、定居或者纵火。

又或想像一条人行道有些许纸屑，如果无人清理，不久后就会有更多垃圾，最终人们会视为理所当然地将垃圾顺手丢弃在地上。

维基百科

因为既然有人选择了“短视”，并且还得益了，那么知道这件事的人不选它，其它对他来说就是一个“损失”。

人性又是厌恶损失的，导致了在大脑的思想斗争中，「大脑边缘」会占据上风。

随着作出这样选择的人越多，越会激发人性的另一个特点——「从众效应」，加速进入到一个“不可收拾”的境地。

生活中，「破窗效应」的例子也有很多。比如，行人穿马路，每次红灯变绿灯的前几秒（特别是车少的时候），人们就开始蠢蠢欲动。当第一个人一旦开始闯红灯，后面的人也会立马跟上。这个景象在早些年更加严重。

还有诸如，排行榜靠买量刷量，公司业绩靠造假等等大量“短视”行为逐渐形成一种风气的情况。按规则办事的人往往会吃亏，甚至连“汤都喝不到”。

“短视”的长期副作用

这种打破规则的事情如果一直不被重视的话，长期以往，造成的后果会更严重。

首先会对制定规则的公共组织的公信力造成影响。而建立信任的成本是非常高的，像爬楼梯一样，降低起来很快，但增长起来则困难得多。

并且，一个公共组织的公信力一旦不足，那么后续制定的规则，会被人认为是形式主义，而不受重视。

这个惯性一旦形成，再想逆转就难了。

其次，个体做事风格的随意性增大。大家都按照自己的想法来做事就好了，反正是可以不安规则来的，但是呢每个人对同一件事的看法又是有或多或少的差别的。

此时，人与人之间协作的内耗开始快速增加，开始相互推诿，做一件事的成本可能反而远大于之前遵守看似冗长的规则的好多倍。选择“短视”所带来的短期利益会消失殆尽，甚至倒亏。

那应该怎么来考虑这个问题呢？

一点思路和建议

首先我们一定要心里有一个信念。就是，任何问题如果只是在一个维度上考虑，大多是不对的。

因为任何事物都有两面性，甚至是多面性的。

所以，当你因为一个因素就得出了一个结论或者观点，首先要停下来考虑一下。“我是不是短视了？”。

最简单，也是最容易被忽略的两个考虑的维度，就是「时间」和「空间」。

如果说一个问题是一个点，那么时间就是基于这个点的一条纵线，空间就是基于这个点的条横线。

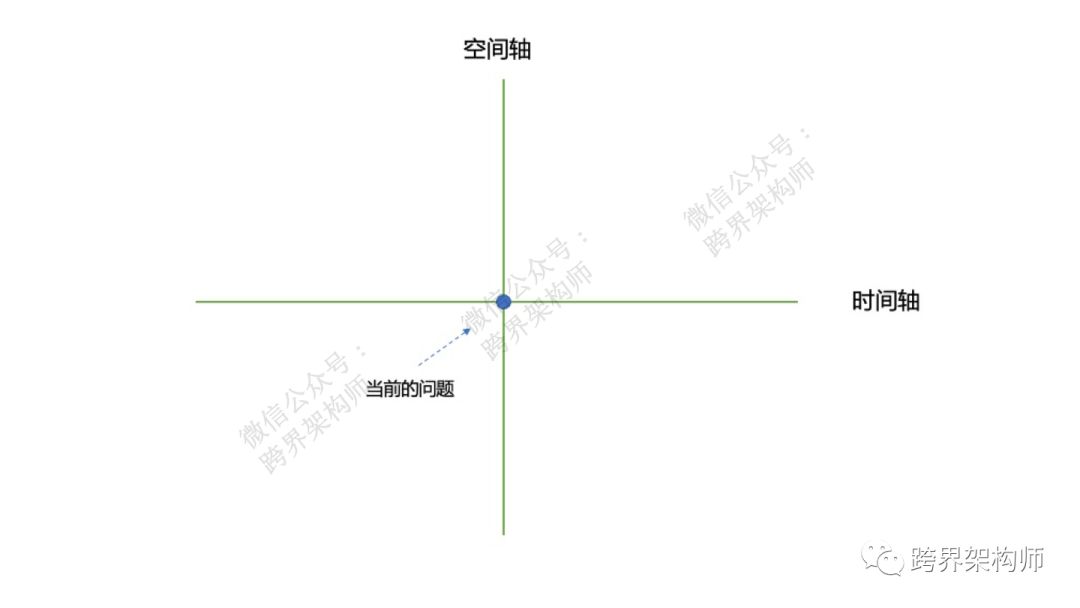
先来说说「时间」，还是拿文章最开始的例子。

比如，我们可以考虑一下，如果这么干了，后续发生一些相关的问题，排查问题起来成本是不是会增加？

毕竟当时临时做这事的人不是专业的，出错的概率也会增加。

除此之外，后续排查相关问题的沟通成本也会增加，多了一个干系人。而且这个干系人还有可能离职了，又因为临时做事，也没有留下什么交接的信息。

如果站在「空间」维度的话，可以再思考一下这样的决定是否会对其它方面产生影响？

比如，部门B要临时接的这个活，是否完全覆盖了原本部门A要做的。如果其中还涉及到一些原本部门A要和部门C、部门D沟通的事情，也要转由给部门B去沟通。这个影响面会不会太大，不确定性会不会太高？反而得不偿失？

Z哥我从这两个维度出发，帮你提炼了两个最佳实践：

1. 一个规则所涉及的范围越大（组织规模呈正相关），越不应该为了短期利益被破坏。

2. 如果坚守规则所损失的短期利益可以承受，还是选择按规则办事。毕竟规则中蕴含着前人的思想结晶，不应该如此轻易的否定它、打破它。

破坏规则的另一面

不过，破坏规则的好处也是显而易见的，更快速、更方便、更高效、更低的成本等等。

在我们的生活中，也能感受到它的好处。比如，

• 「托关系」办事的文化，的确打破了规则，但是减少了建设信任、过滤筛选的环节，让不熟悉的两个人之间协作的成本大大降低了。其实也就是减少了资源浪费。

• 早晚高峰时期，交警和交管通过人为的干预，对车流进行效率最大化的实时管控，从而避免了拥堵的车道在“干等”空闲车道的绿灯的情况。

所以，到底是什么方式最好，没有放之四海而皆准的标准。很大程度上也和每个人的价值观有关。

有的人就觉得过好眼前更重要，未来会怎么样还不知道呢？而有的人则可能更倾向先苦后甜，现在的坚持为的是更好的未来。

不过，如果发现一个规则经常被用同一种方式打破，那么可以考虑一下将它作为新的规则，来指导后续的思考、做事的方向。

总结

好了，总结一下。

这篇我们讨论了到底「该不该破坏规则」的问题。

首先，聊了很多关于破坏规则的副作用，短期的和长期的。

随后，分享了我建议的考虑两个视角，时间和空间。

明白了这些之后，相信你对「该不该破坏规则」的把握就更有谱了。

希望对你有所启发。

推荐阅读：

• 一句话概括4本管理著作

• 一份好的工作总结才能帮你升职加薪

原创不易，如果你觉得这篇文章还不错，就「在看」或者「分享」一下吧。鼓励我的创作 ：）