常用开发模式

一、瀑布式开发

　　瀑布式开发是在1970年提出的软件开发模型，是一种较老的计算机软件开发模式，也是典型的预见性的开发模式，在瀑布式开发中，开发严格遵循预先计划的需求分析、设计、编码、集成、测试、维护的步骤进行，步骤的成果作为衡量进度的方法。瀑布式开发最早强调系统开发应有完整的周期，且必须完成完整地经历每个周期内的每个阶段，并系统化地考量分析所设计的技术、时间与资源等。

　　瀑布式开发的主要问题是它严格分级导致自由度降低，在需求不明确并且在项目进行过程中可能有变化的情况下基本上是不可行的。

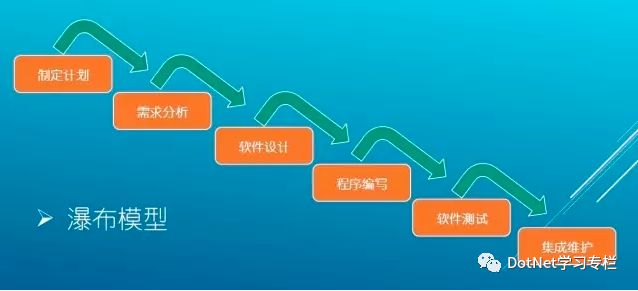
（瀑布式开发模式图）

二、迭代式开发

　　迭代式开发也称迭代增量式开发，是一种与瀑布式开发相反的软件开发过程，它弥补了瀑布式开发方式的一些弱点，有更高的成功率。在迭代式开发中，整个开发工作被组织成一系列短小的、固定长度的小项目，每次迭代都包括需求分析、设计、实现与测试。采用迭代式开发时，工作可以在需求被确定之前启动，并在一次迭代中完成系统的一部分功能或业务，再通过客户的反馈来细化需求，并开始新一轮的迭代。

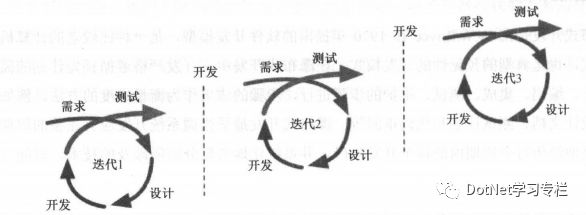（迭代式开发模式图）

　　迭代式开发有以下的特点：

　　　　1）每次只设计和实现产品的一部分

　　　　2）一步一步地完成

　　　　3）每次设计和实现一个阶段，这叫作迭代

三、螺旋式开发

　　螺旋式开发兼顾了快速原型的迭代特征及瀑布模型的系统化和严格监控，其最大的特点是引入了其他模型不具备的风险分析，使软件在无法排除重大风险时有机会停止，以减少损失。同时，在每个迭代阶段构建原型是螺旋模型用来减少风险的方法。螺旋模型更适合大型的高昂的系统级的软件开发，一开始应用的规模很小，当项目被定义得更好、更稳定时逐渐展开。其核心在于不需要在刚开始时就把所有的事情都定义清楚，可以先定义最重要的功能去实现，然后听取客户的意见再进行下一个阶段，如此不断循环、重复，直到得到满意的产品。螺旋模型在很大程度上是一种风险驱动的方法体系，因为在每个阶段及经常发生的循环之前，都必须先进行风险评估。

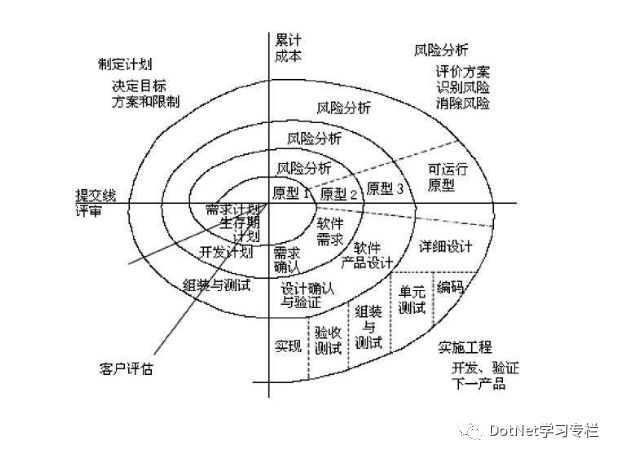（螺旋模型图）

　　螺旋模型具有如下的特点：

　　　　1）制定计划：确定软件目标，选定实施方案，搞清楚项目开发的限制条件

　　　　2）风险分析：分析、评估所选方案，考虑如何识别和消除风险

　　　　3）实施工程：实施软件开发和验证

　　　　4）客户评估：评价开发工作，提出修正意见。制定下一步计划

四、敏捷软件开发

　　敏捷软件开发又成敏捷开发，是一种从1990年开始逐渐引起人们广泛关注的新型软件开发方式，具有应对快速变化的需求的软件开发能力，相对于非敏捷开发，更强调程序员团队与业务专家之间的紧密协作及面对面沟通，比单纯通过书面文档沟通更有效，能更频繁地交付新的软件版本，使自我组织、自我约束的团队能够更好地适应需求的变化，也更关注软件开发过程中人的作用。

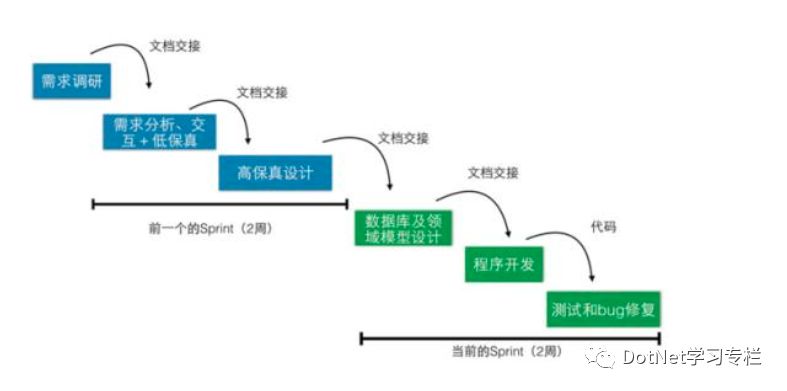
　　敏捷软件开发有如下特点：

　　　　1）首要任务是尽早地、持续地交付可评价的软件，使得客户满意

　　　　2）乐于接受需求变更，即使在开发后期也是如此，敏捷软件开发能够驾驭需求的变化，从而为客户赢得竞争优势

　　　　3）频繁交付可使用的软件，交付的间隔越短越好，可以从几个月缩减到几个星期

　　　　4）在整个项目开发期间，业务人员和开发人员必须朝夕工作在一起

　　　　5）围绕那些有推动力的人们来构建项目。给予他们所需的环境和支持，并且相信他们能够把工作做好

　　　　6）可使用的软件是进度的主要衡量指标

　　　　7）提倡可持续发展

　　　　8）为了增强敏捷能力，应持续关注技术上的杰出成果和良好的设计

　　　　9）简洁，最小化那些没有必要投入的工作量是至关重要的

　　　　10）最好的架构、需求和设计都源于自我组织的团队

 　　对比以上4种开发模式，总结如下：

　　　　1）瀑布式开发：在从需求到设计、从设计到编码、从编码到测试、从测试到提交的每个开发阶段都要做到最好，特别是在前期阶段设计得越完美，提交后的损失就越少。然而现在的系统很复杂且多变，所以很难在现实中应用瀑布式开发。 

　　　　2）迭代式开发：不要求每个阶段的任务都做到最好，可以容忍一些不足，先不去完善它，将主要功能先搭建起来，以最短的时间及最少的损失完成一个不完美的成果直至提交，然后通过客户或用户的反馈，在这个不完美的成果上逐步进行完善。 

　　　　3）螺旋开发：在很大程度上是一种风险驱动的方法体系，因为在每个阶段及经常发生的循环之前，都必须先进行风险评估。 

　　　　4）敏捷开发：和迭代式开发相比，两者都强调在较短的开发周期内提交软件，但是敏捷开发的周期可能更短且更强调队伍中的高度协作。敏捷方法有时被误认为是无计划性和纪律性的方法，实际上更确切的说法是敏捷方法强调适应性而非预见性，适应性的方法主要用于快速适应需求的变化。当项目的需求有变化时，团队能够迅速应对新的需求 。 

　　在一般公司里，采用敏捷开发和不断迭代开发的方式较多，而且效率高、效果明显。因为之前做的系统业务单一、逻辑简单、用户量少，项目团队的规模一般在10-30人，现在的系统要面对不同用户的定制化开发，业务变得越来越复杂，功能越来越多，如果整个系统耦合在一起，必定会牵一发而动全身，导致系统维护困难，同时每个公司面临着人员的频繁流动、系统文档不完善或多次转手丢失等情况，以至于新来的人员很难快速上手。因而，人们开始思考如何高效地解决复杂的大型系统开发模式。

 

说明：

　　1、参考书籍：《分布式服务架构：原理、设计与实战》《微服务架构与实践》

　　2、如有不合适的地方请反馈。综合后更改。

　　3、文中图片来源于百度图片