今天（北京时间 2019 年 9 月 5 日），微软发布了 Visual Studio Code 1.38 版本。此版本主要更新的内容包括：

• Preserve case for global search and replace - 进行全局替换字符串时保留大小写。

• Settings editor string array validation - 在配置编辑器中进行字符串数组的验证：最小值，最大值，enum 以及 glob。

• Adjust cursor surrounding lines - 设置在滚动时光标选中的行数。

• Copy and revert in the diff editor - 在 diff editor 中方便地复制或者恢复被删除的内容。

• Go to Line supports negative line numbers - 快速跳转到文件末尾。

• MDN Reference link for HTML and CSS - 在 IntelliSense 中显示 MDN 文档。

• Add missing await Quick Fix - 在异步代码中，快速修复缺失的 await 代码。

• Debugging data breakpoints - 当跟踪的变量变化时，中断调试器。

• VS Code icon repository - 官方图标库发布。

• Alpine Linux distro support - 远程开发支持 Alpine Linux。

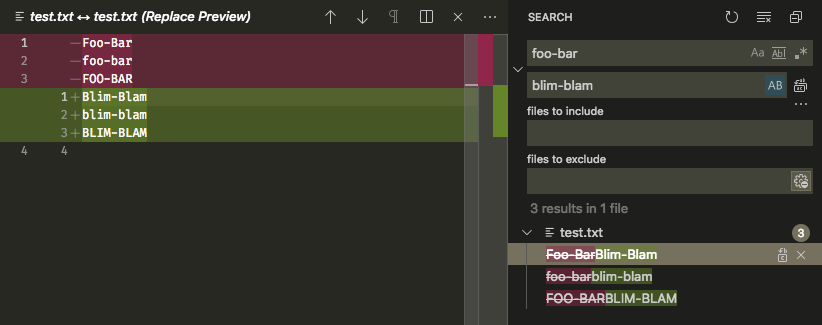
替换字符串时保留大小写

在 1.37 版本中，支持了替换字符串时保留大小写。如今，在进行全局替换字符串时，大小写也会保留。同时，现在也支持保留连字号分隔的单词。

光标行数设置 (scrollOff)

现在，可以通过 editor.cursorSurroundingLines 来设置在滚动时，光标所选中的行数。这就是 Vim 编辑器的 scrollOff 功能。

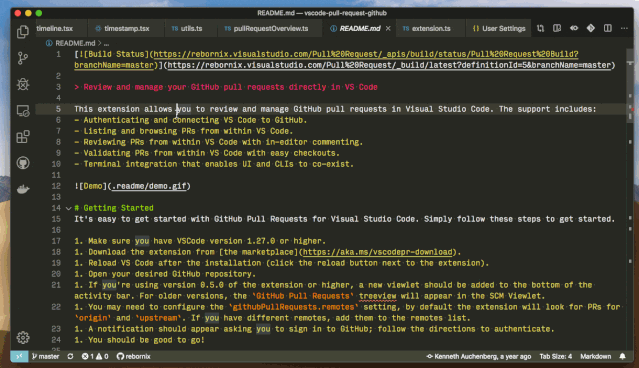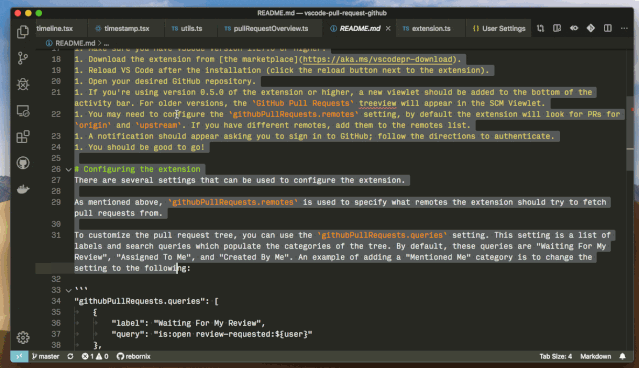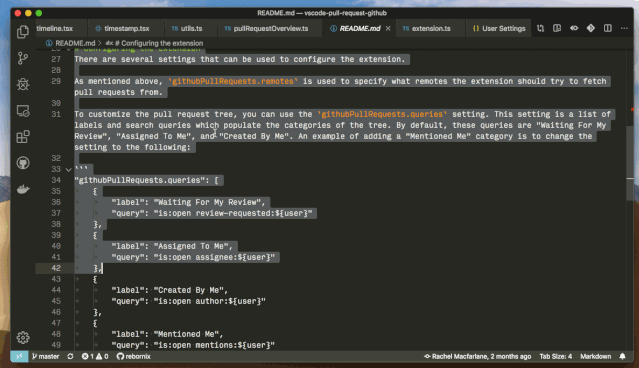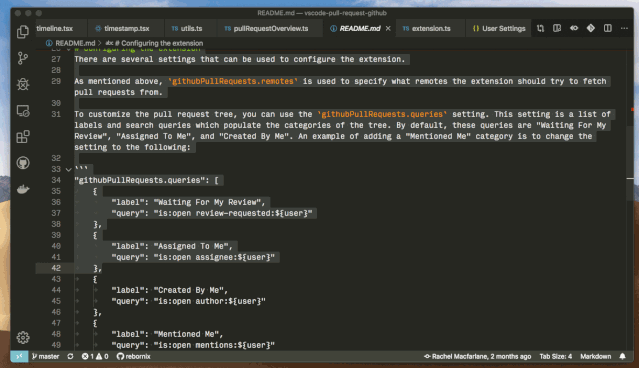
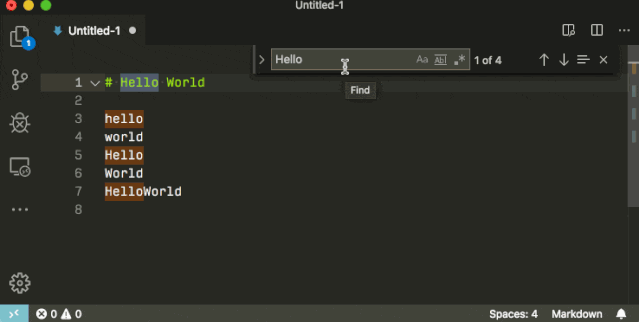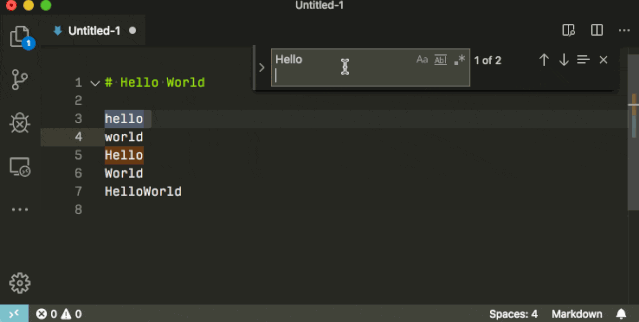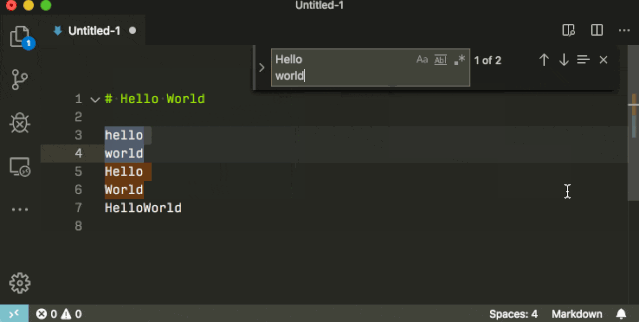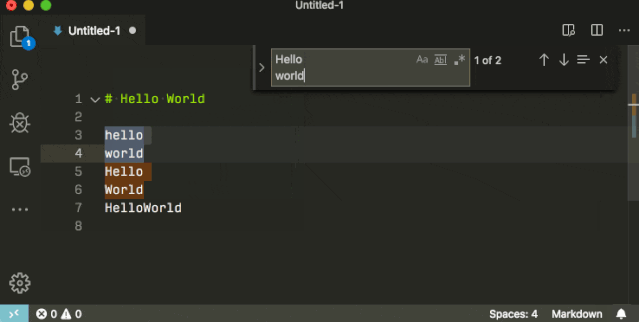
多行搜索

通过 Ctrl+Enter，你可以在搜索框里换行，然后进行多行搜索。

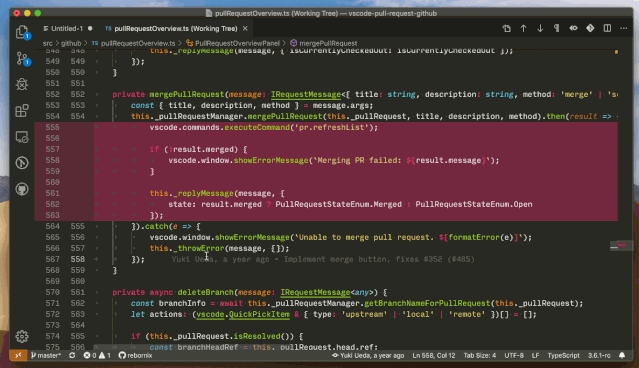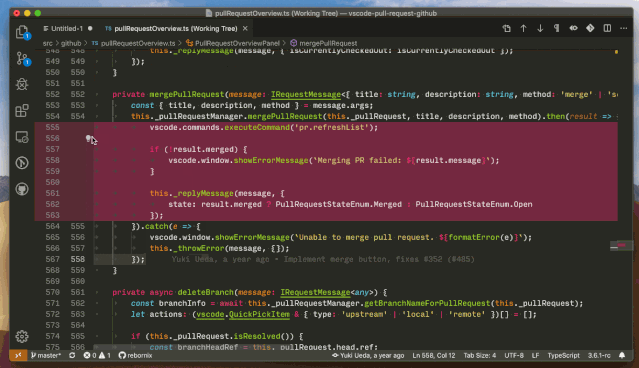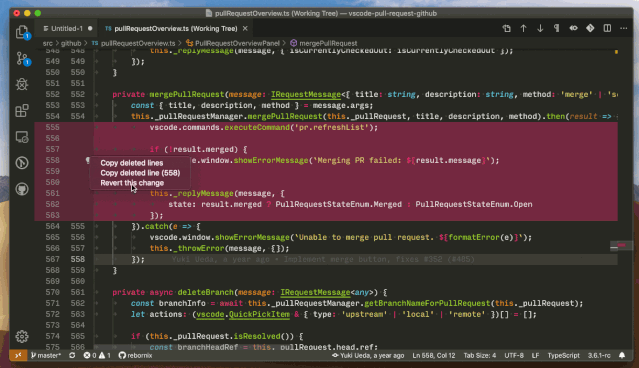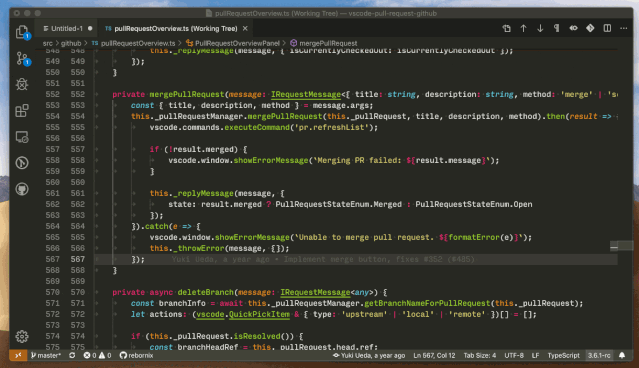
在 diff editor 中复制或恢复

HTML 和 CSS 的 MDN 参考文档

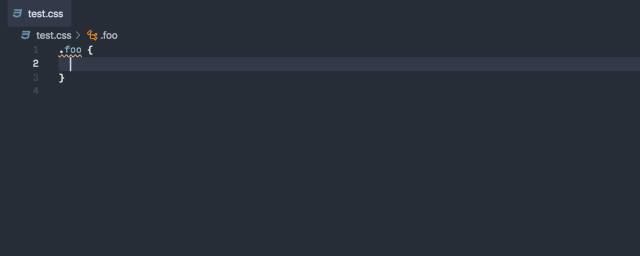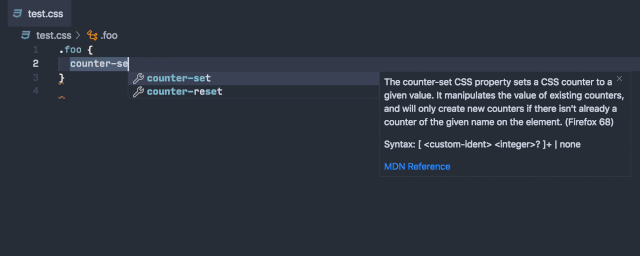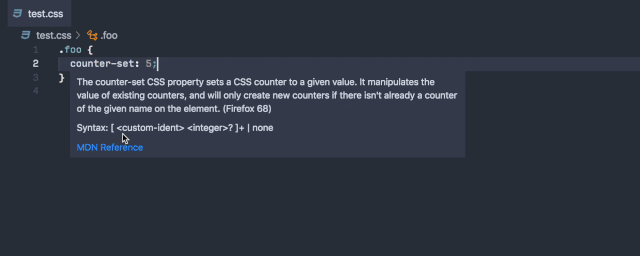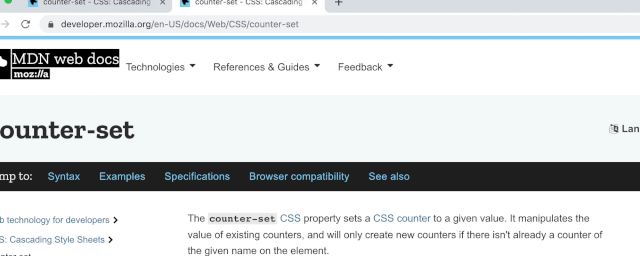
在编写或者悬停在 HTML/CSS 时，会有一个指向 MDN 文档的链接。

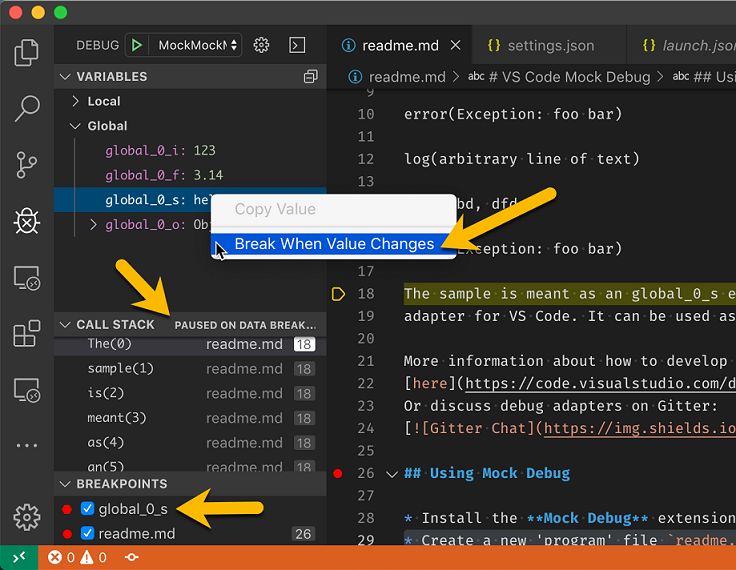
Data Breakpoints

可以针对一个变量添加断点。当跟踪的变量变化时，中断调试器。

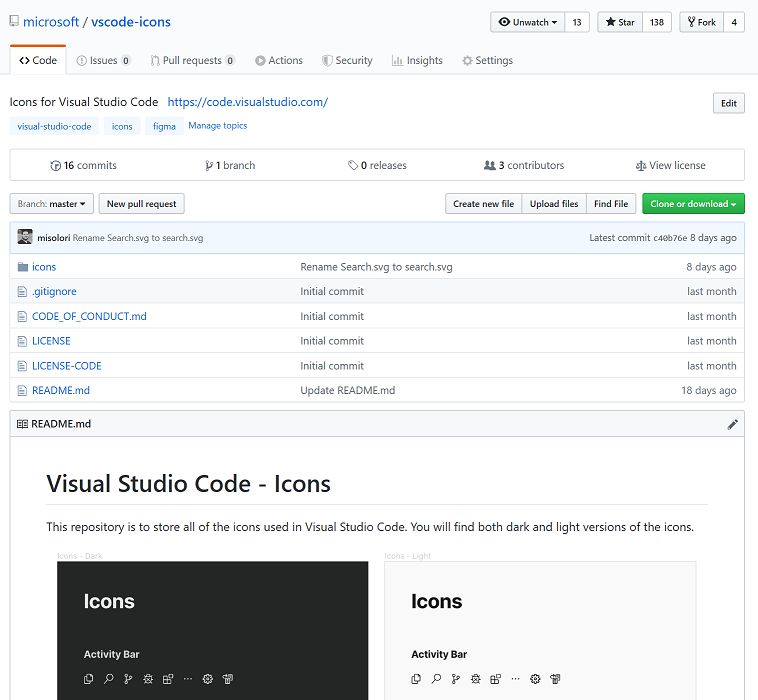
VS Code 图标库

https://github.com/microsoft/vscode-icons

更多完整内容，请查看 VS Code 官网的 Release Notes：

https://code.visualstudio.com/updates/v1_38