最近感悟天命，偶有所得，故而打算收徒若干，以继吾之传承。

有缘者，可破瓶颈，职场巅峰指日可待。

 

入门基本要求：

---

 1、工作经验：1年或以上。

 2、拜师费用：3999元（RMB）。

 

传承说明：

---

1、收徒人数：限10人。

2、1vs1指导：1个月内让您学会4.1~4.7中所有内容

3、出师：精通.NETCore，精通前后分离与Window负载均衡技术；提高职场竞争力。

4、教学成果 (精通如下技术) 

4.1、.NETCore、.NETCore WebApi

4.2、Vue、前后分离开发技术，ELE-UI设计

4.3、JwtToken认证

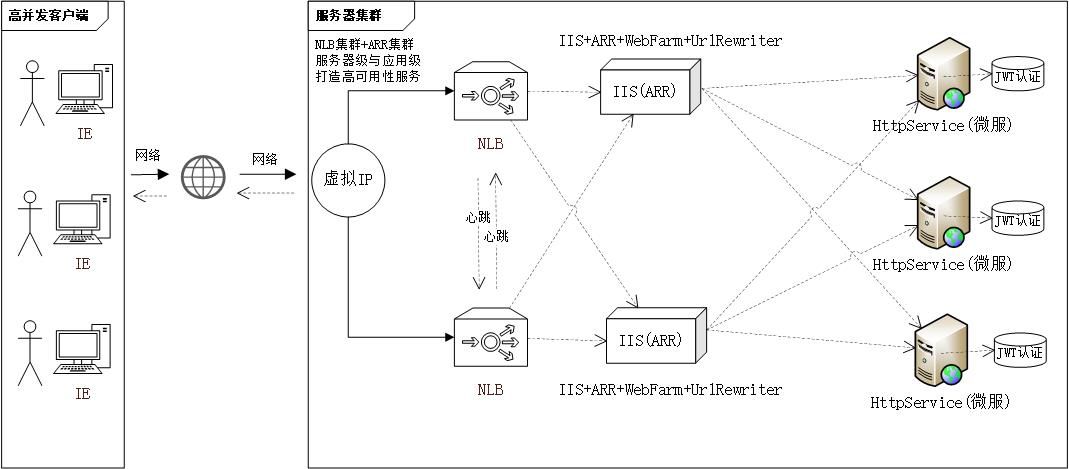
4.4、IIS负载均衡高级技术

4.5、服务器集群技术

4.6、DapperORM技术

4.6、分布式主键算法

4.7、给予.NETCore开发框架系统（Window负载均衡-通用版本）源码一套，用于深度研究。（声明：仅限个人学习与研究用途、不得转发他人或网络上）

.NETCore开发框架系统（Window负载均衡架构-通用版）演示视频如下：http://agile.letyouknow.net

 

联系方式：

---

扫码联系我，备注：.NET拜师

 

备注：

心不诚者，喜欢问来问题去，勿扰。

对我来说，错过你，也就是一次师徒缘份的问题，但却省了时间和精力。

对你来说，错过我，就是失去一次往更高可能职位的机会。

 

有缘者来，无缘者去；

众生皆客，唯传承留。