一、关于RPC的调用

　　1. 调用者（客户端Client）以本地调用的方式发起调用；
　　2. Client stub（客户端存根）收到调用后，负责将被调用的方法名、参数等打包编码成特定格式的能进行网络传输的消息体；
　　3. Client stub将消息体通过网络发送给服务端；
　　4. Server stub（服务端存根）收到通过网络接收到消息后按照相应格式进行拆包解码，获取方法名和参数；
　　5. Server stub根据方法名和参数进行本地调用；
　　6. 被调用者（Server）本地调用执行后将结果返回给server stub；
　　7. Server stub将返回值打包编码成消息，并通过网络发送给客户端；
　　8. Client stub收到消息后，进行拆包解码，返回给Client；
　　9. Client得到本次RPC调用的最终结果。

　　参考https://www.cnblogs.com/FG123/p/10261676.html

　　参考https://www.jianshu.com/p/bb9beca7f7bc 第四节

二、关于RPC调用方式的思考（为什么要用代理类）

RPC的方便之处我们已经看到了，

假设在系统中要调用多个服务，如果写一个函数，每次将这个服务的名字，参数，和其他信息通过一个方法来调用远程服务，假设这个方法叫做getService(methodname,object[],参数3，参数4)    

我们在各个消费类中来调用这个方法似乎也能得到结果。

在每个调用远程服务的地方都要反射出 类的方法名称，参数等其他信息以能传给getService 是不是很麻烦？

要知道远程服务每个服务返回的结果不会是一样的类型，那我们在客户端还要每次都转换getService的结果，是不是很麻烦？

有没有好的解决方案？

　　--请使用代理类，我们在代理类中反射代理接口得到这个方法的各种属性（名称&参数&其他），远程调用传递给远程服务，并转换得到的结果。看起来这种方法和上文的getService 差不多嘛！那我们为什么要使用代理类呢？（我也不知道，但看起来很吊的样子。）这看起来并没有很好的样子，况且如果有多个类要调用远程服务，那岂不是要写很多代理类？

思考：调用getService 后每次都要在消费类中转换结果，使用代理类后将这个转换过程放入了代理类中，这样消费类就不用关注RPC的调用结果的类型的转换了。

于是人们发明了动态代理   _{--来自《鲁迅先生说革命》}

人们发现每个类都要写个代理。现在小明要在项目中写1000个代理类，直接气炸了，对！炸了!。

经过了N代的小明客户钻研和发现，总结了一套可以很省力气的方法。--动态代理

简单的来说：动态创建代理类（https://www.cnblogs.com/netqq/p/11452374.html），这样就不用给每个消费类都写一个代理类了，是不很爽

三、动态代理与RPC

 在网上找到了一个简单的RPC 示例，非常适合初学者学习  https://github.com/Coldairarrow/DotNettyRPC 

 下载项目后先运行 Server 项目，再运行client项目

看到再server的控制台上输出了hello 字符串。这是客户端程序调用了server的IHello.SayHello()的服务输出的。

我们来看下作者的客户端调用

 

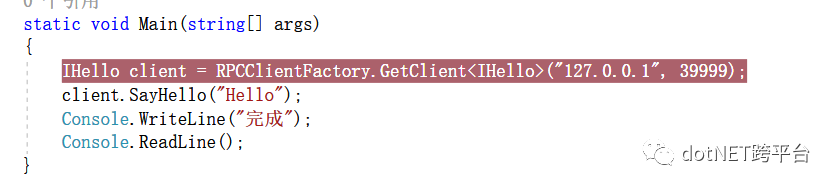
RPCClientFactory源码如下

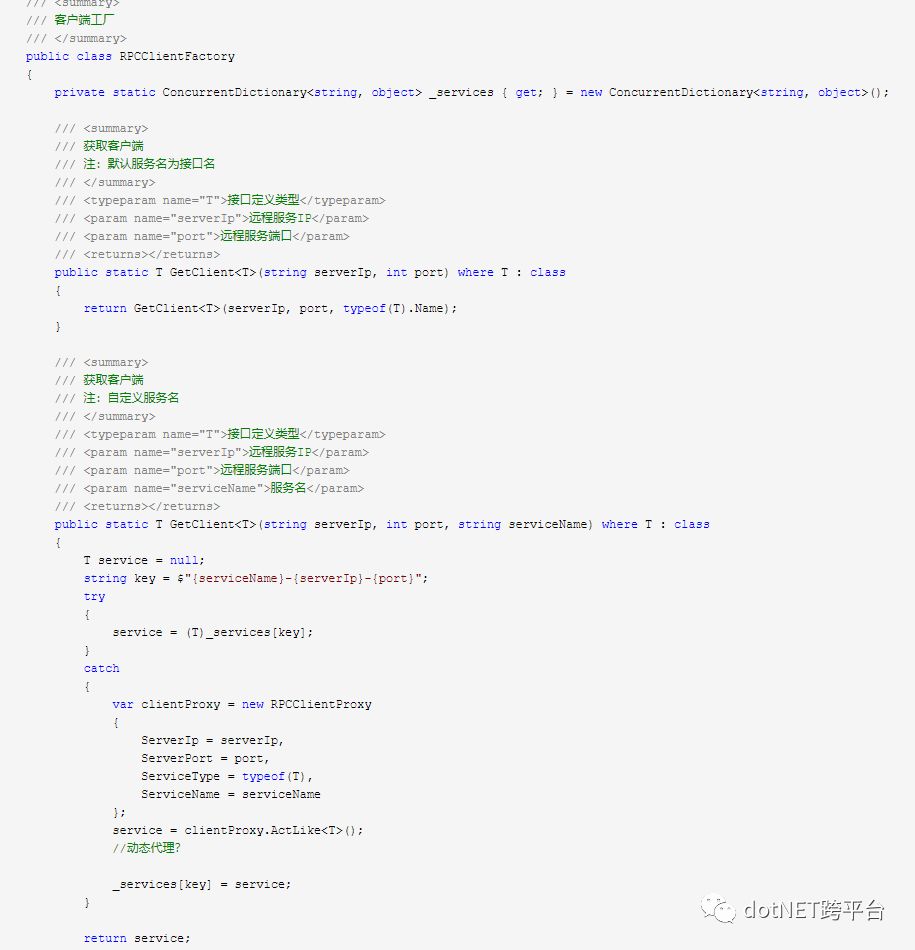
在示例中，程序调用的GetClient 

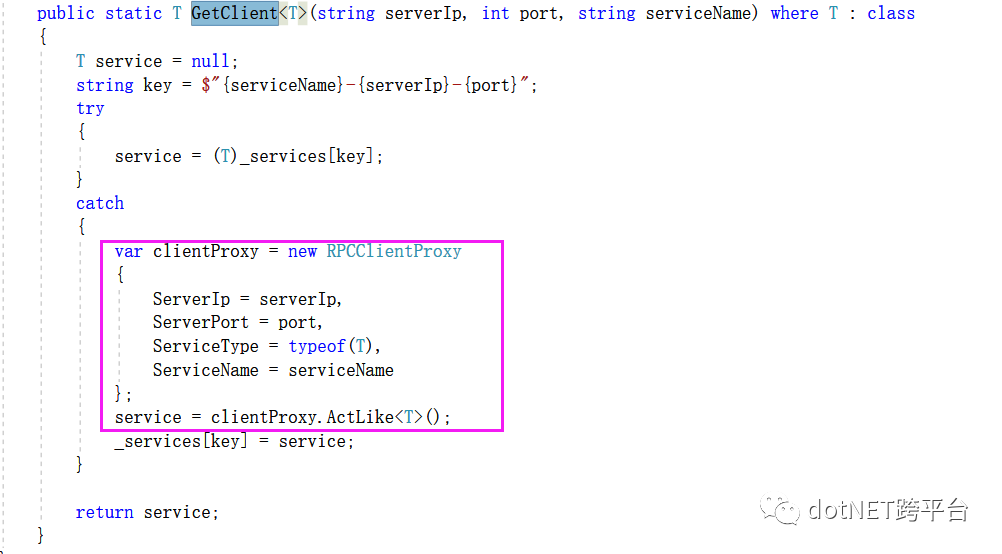
 实际上也是动态生成的代理类，返回了IHello类型的对象。

我们先抛开该作者的程序，用我们自己的动态代理类来实现相同的效果。

在DotNettyRPC项目中添加ProxyDecorator<T> 类。   需要nuget下载System.Reflection.DispatchProxy.dll

在添加ProxyDecorator 和编译的时候会遇到问题，我们将server、 client项目和DotNettyRPC  转为NETCORE项目才能正常执行 ，因为 System.Reflection.DispatchProxy.dll 只NETCORE 类库，不支持NET Framework项目

ProxyDecorator<T>  源码

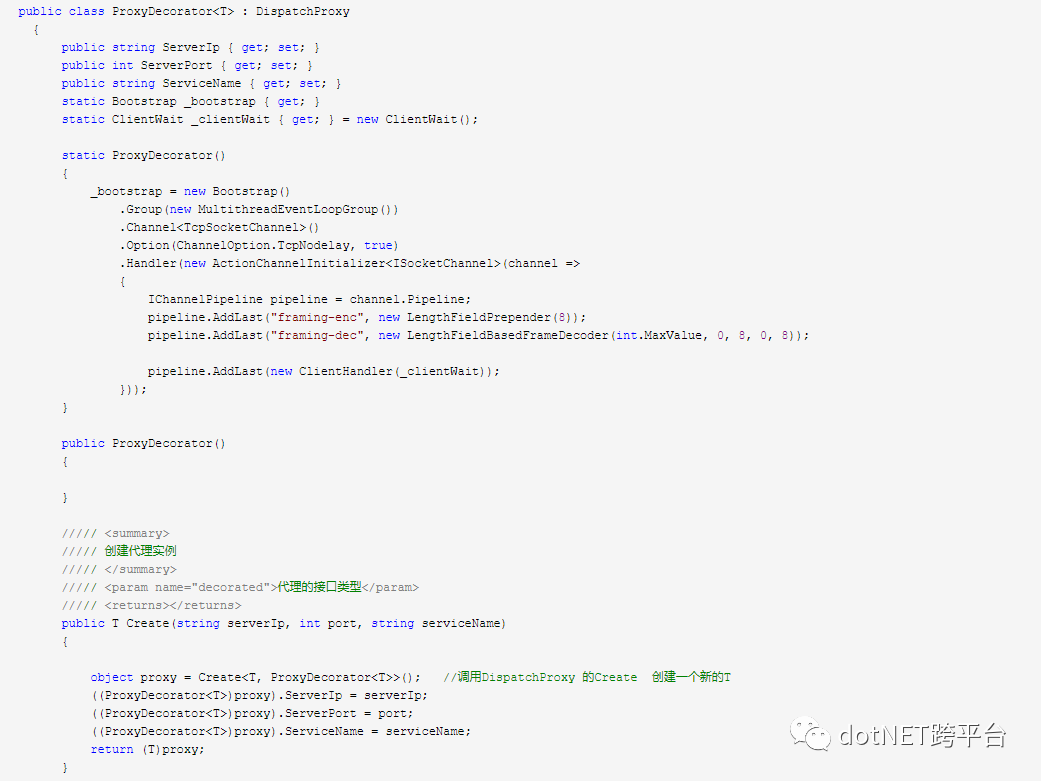
这个类的源码与上一篇反向代理文章中所讲的核心区别是 Invoke 的实现，上篇文章中其调用的是本地的一个类实体的方法，本文中其调用的是远程服务中的类实体的方法

client调用代码如下

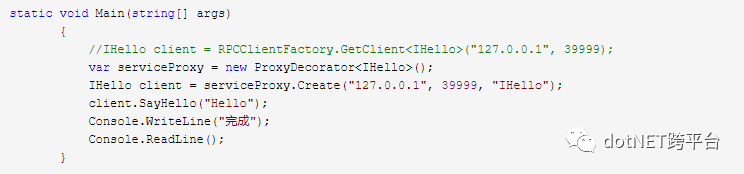
 重新启动Server 和Client 执行效果如下

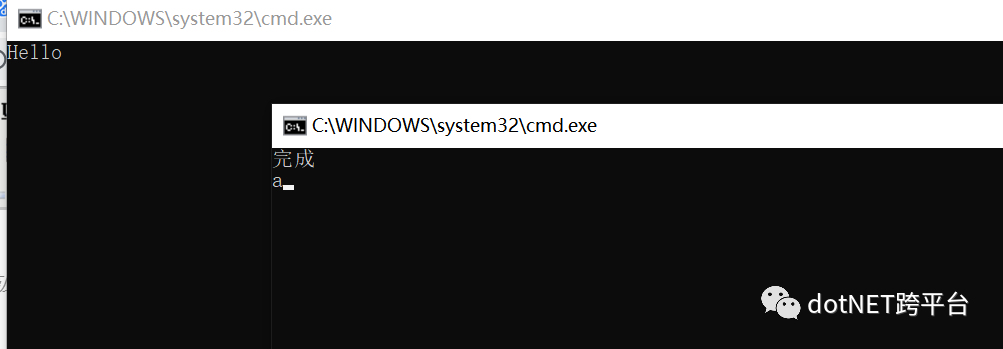
和原作者的执行结果一致，那么我们换个接口来试试：创建IMail  和Mail两个类，并包含一个成员string  Send(string  name)//IMail和Mail的成员  

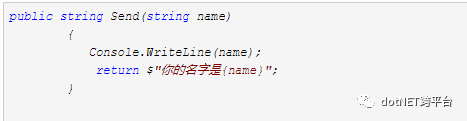
Client端调用代码

服务端添加服务监控

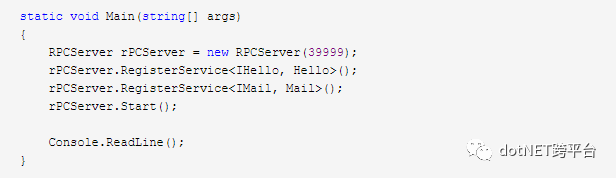
预计客户端输出：

你的名字是张三丰

完成 

服务端输出是：

张三丰

我们先后启动server 和 client 两个端来看看

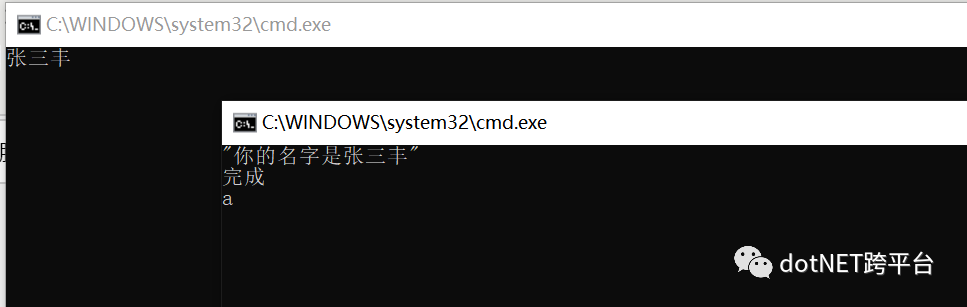
至此动态代理的应用示例已经演示完毕。

在查看   寒空飞箭   git 源码时候我们发现  RPCClientProxy 类和我们的ProxyDecorator<T> 类  实现了相同的效果，寒空飞箭的实现方式也是很令人振奋，独辟蹊径，非常值得学习。下篇文章将会分析他的用法。感兴趣的可以自行查看作者的源码。

参考文献：

https://www.cnblogs.com/coldairarrow/p/10193765.html

 说明：

RPC功能的实现是直接引用作者 寒空飞箭 的代码，对此向 寒空飞箭 表示感谢

相关文章：

• netcore 之动态代理（微服务专题）

原文链接：https://www.cnblogs.com/netqq/p/11462054.html

---

.NET社区新闻，深度好文，欢迎访问公众号文章汇总 http://www.csharpkit.com