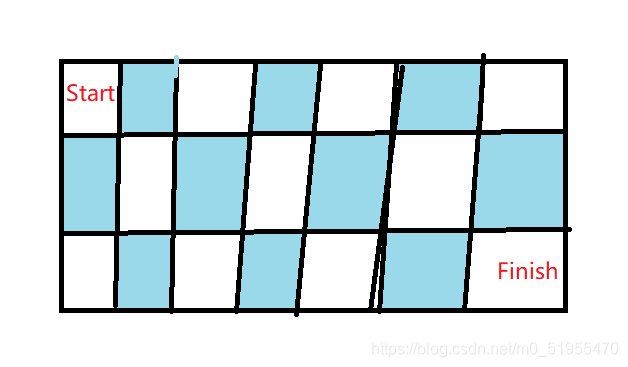
一个机器人位于一个 n * m 网格的左上角 （起始点在下图中标记为“Start” ）。(n表示行，m表示列)

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

问总共有多少条不同的路径？

数据范围：
n <= 100,m <= 100;

解题思路：
首先我们定义dp[i][j]表示机器人走到（i,j）这个位置的走法总数，
然后我们想到机器人每次只能向下或者向右移动一步，那么这个位置只可能来自上面走下来的，或者左边走过来的，故容易想到关系表达式为dp[i][j] = dp[i-1][j]+dp[i][j-1]，然后我们想想初始化问题，假如i = 0，那么i-1就会为负数，数组会越界，我们可以这样初始化：

for (int i = 0; i < n; i++)dp[i][0] = 1;//相当于最左边那一列，机器人只能往下走，故走法只有一种for (int i = 0; i < m; i++)dp[0][i] = 1;//相当于最上面那一行，机器人只能往右走，故走法只有一种

代码如下：

#include <iostream>
using namespace std;
const int N = 1010;
int dp[N][N];int main() {int n, m;cin >> n >> m;for (int i = 0; i < n; i++)dp[i][0] = 1;for (int i = 0; i < m; i++)dp[0][i] = 1;for (int i = 1; i < n; i++)for (int j = 1; j < m; j++) {dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}cout << dp[n - 1][m - 1] << endl;return 0;
}