题目描述
把1~16的数字填入4x4的方格中，使得行、列以及两个对角线的和都相等，满足这样的特征时称为：四阶幻方。
四阶幻方可能有很多方案。如果固定左上角为1，请计算一共有多少种方案。
比如：
1 2 15 16
12 14 3 5
13 7 10 4
8 11 6 9
以及：
1 12 13 8
2 14 7 11
15 3 10 6
16 5 4 9
就可以算为两种不同的方案。
输出
请提交左上角固定为1时的所有方案数字

刚开始，以为又是水题，然后…原来15个数的全排列这么大，next_permutation的做法不行！！！
代码如下：

#include <iostream>
#include <algorithm>
using namespace std;
int b = 1;
int a[] = {2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16};
int ans;bool check() {int r1 = b + a[1] + a[2] + a[3];int r2 = a[4] + a[5] + a[6] + a[7];int r3 = a[8] + a[9] + a[10] + a[11];int r4 = a[12] + a[13] + a[14] + a[15];int r5 = b + a[5] + a[10] + a[15];int r6 = a[3] + a[6] + a[9] + a[12];if (r1 == r2 && r1 == r3 && r1 == r4 && r1 == r5 && r1 == r6 &&r2 == r3 && r2 == r4 && r2 == r5 && r2 == r6 &&r3 == r4 && r3 == r5 && r3 == r6 && r4 == r5 && r4 == r6 &&r5 == r6 ) {return true;}return false;
}int main() {do {if (check()) {ans++;}} while (next_permutation(a, a + 15));cout << ans << endl;return 0;
}

所以我们只能用dfs了，还需要剪枝不然会超时。

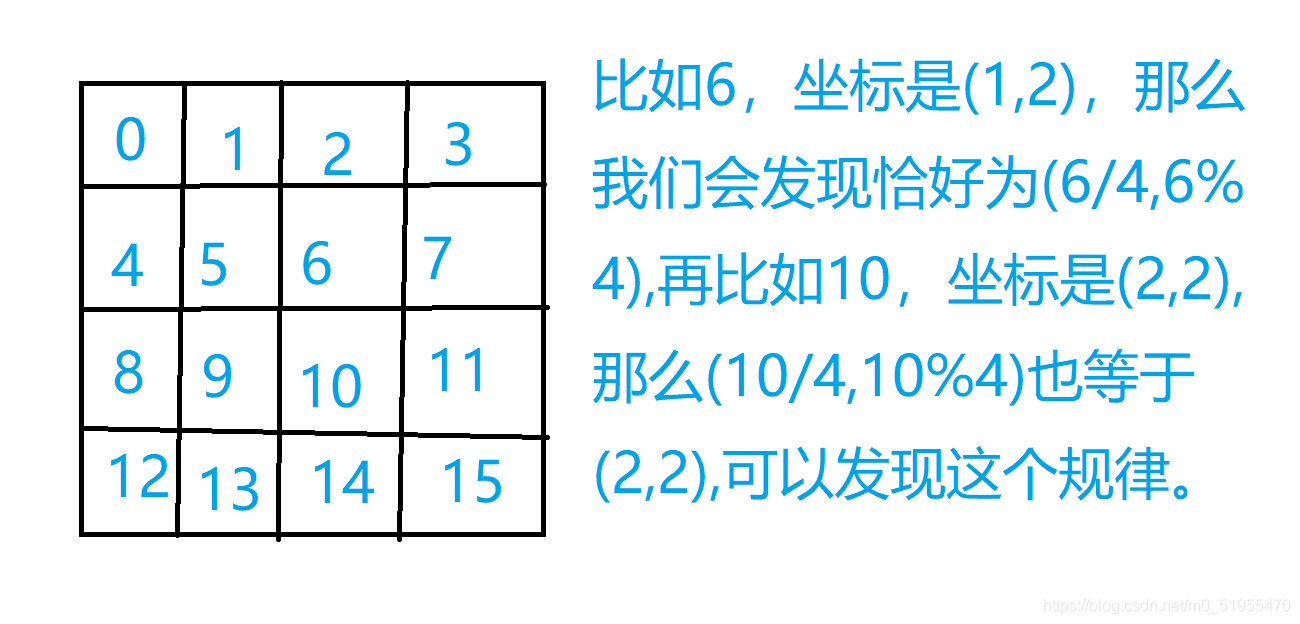
解题思路：
事实上，n阶幻方，都有其各自的固定值(每行相加或者每列相加或者某一条对角线相加的和)，4阶幻方的和为34，故我们可以这样剪枝，当最开始的这一行填满后，每次填满一行后判断上一行每个数相加是否等于34，然后，在接下来的check环节，也可以判断某一行，某一列看是不是等于34，不是就return false

代码如下：

#include <iostream>
using namespace std;
const int res = 34;
const int N = 20;
int a[N][N];
int ans;
bool st[N];bool check_row(int n) {//判断行int sum = 0;for (int i = 0; i <= 3; i++) {sum += a[n][i];}return sum != res;
}bool check() {int sum = 0;sum += a[0][0] + a[1][1] + a[2][2] + a[3][3];//对角线if (sum != res)return false;sum = 0;sum += a[0][3] + a[1][2] + a[2][1] + a[3][0];//对角线if (sum != res)return false;for (int i = 0; i <= 3; i++) {//行if (check_row(i))return false;}for (int i = 0; i <= 3; i++) {//列int sum = 0;sum += a[0][i] + a[1][i] + a[2][i] + a[3][i];if (sum != res)return false;}return true;
}void dfs(int u) {if (u == 16) {if (check()) {ans++;}return ;}if (u % 4 == 0) {//剪枝,判断上一行是是否等于34if (check_row(u / 4 - 1))return ;}for (int i = 2; i <= 16; i++) {if (!st[i]) {st[i] = true;a[u / 4][u % 4] = i;dfs(u + 1);st[i] = false;}}}int main() {a[0][0] = 1;dfs(1);cout << ans << endl;return 0;
}