利用栈实现队列

• 上一节中说明了栈的特点 后进先出，我们用数组的方式实现了栈的基本操作api，因此我们对栈的操作是不考虑排序的，每个api的操作基本都是O(1)的世界，因为不考虑顺序，所以找最大，最小值，需要O(n)时间
• 还有与栈相对于的一种数据结构，那就是队列了，队列特点是先进先出，即第一个进去队列的元素会第一个出来，
• 栈和队列虽然特点上相反，当他们也有相互联系，我们利用栈解决如下队列的问题：

问题

• 用两个栈实现一个队列，队列的声明如下：实现两个函数append，del，分别完成队尾插入节点， 队列头部删除节点的功能。
• 队列对象定义：

/*** @author liaojiamin* @Date:Created in 11:37 2021/3/9*/
public class MyQueue {private MyStack<Integer> myStack1;private MyStack<Integer> myStack2;private boolean isAdd;public MyQueue(){myStack1 = new MyStack<>();myStack2 = new MyStack<>();isAdd = false;}public boolean isAdd() {return isAdd;}public void setAdd(boolean add) {isAdd = add;}public MyStack<Integer> getMyStack1() {return myStack1;}public void setMyStack1(MyStack<Integer> myStack1) {this.myStack1 = myStack1;}public MyStack<Integer> getMyStack2() {return myStack2;}public void setMyStack2(MyStack<Integer> myStack2) {this.myStack2 = myStack2;}
}

分析

• 我们需要通过stack1与stack2实现先进先出的队列MyQueue，我们用一个实际案例来分析，
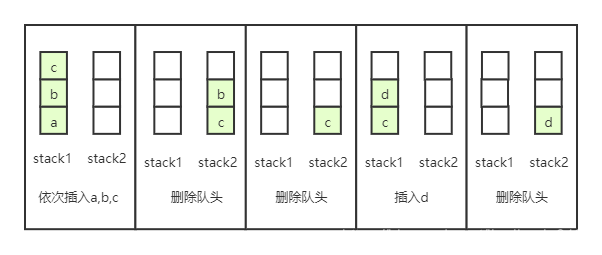
• 首先add 一个元素a到stack1中，在接着，b，c还是到stack1中，此时stack1 中有{a,b,c}，stack2是空的，如下图：
• 此时我们需要删除一个元素。按队列先进先出原则，a需要比b，c先出去，但是此时stack1中c是在栈顶。我们需要反转stacl1
• 如上分析，我们将stack1 中所有元素弹出并依次加入stack2，那么就完成反转的功能，在弹出stack2 中第一个元素。实现删除功能
• 继续删除我们还是直接操作stack2即可
• 这时候再来添加操作，因为需要添加到队尾，此时不能添加到stack2，我们只能再次反转，添加到stack1 中。
• 总结：每次add操作或者del操作之前，判断上次操作是add还是del，如果是不同操作，则反转在对非空栈进行操作，如果是相同操作类型，则直接对非空栈进行操作，无需反转

• 代码实现：

/*** 利用两个栈实现队列* @author liaojiamin* @Date:Created in 11:35 2021/3/9*/
public class StackImpleQueue {private MyQueue myQueue = new MyQueue();/*** 添加元素到队列* */public void append(Integer item){if(isEmpty()){myQueue.getMyStack1().push(item);return;}//上次是append，无需changeboolean needChange = !myQueue.isAdd();MyStack<Integer> notEmpty = change(needChange);notEmpty.push(item);}/*** 从队列中删除位置* */public Integer del(){if(isEmpty()){return -1;}//上次是add则需要changeMyStack<Integer> notEmpty = change(myQueue.isAdd());return notEmpty.pop();}/*** 队列是否为空*/public boolean isEmpty(){return myQueue.getMyStack1().isEmpty() && myQueue.getMyStack2().isEmpty();}/*** 将非空栈中数据弹出并添加到另一个栈* */public MyStack<Integer> change(boolean needChange){if(isEmpty()){return myQueue.getMyStack1();}MyStack<Integer> emptyStack = myQueue.getMyStack1().isEmpty() ? myQueue.getMyStack1() : myQueue.getMyStack2();MyStack<Integer> notEmptyStack = myQueue.getMyStack1().isEmpty() ?  myQueue.getMyStack2() : myQueue.getMyStack1();if(needChange){while (!notEmptyStack.isEmpty()){emptyStack.push(notEmptyStack.pop());}//切换操作标记位myQueue.setAdd(!myQueue.isAdd());return emptyStack;}return notEmptyStack;}public static void main(String[] args) {StackImpleQueue stackImpleQueue = new StackImpleQueue();stackImpleQueue.append(1);stackImpleQueue.append(2);stackImpleQueue.append(3);System.out.println(stackImpleQueue.del());System.out.println(stackImpleQueue.del());stackImpleQueue.append(4);System.out.println(stackImpleQueue.del());System.out.println(stackImpleQueue.del());}}

上一篇：数据结构与算法–简单栈实现及其应用
下一篇：数据结构与算法–链表实现以及应用