再谈递归与循环

• 在某些算法中，可能需要重复计算相同的问题，通常我们可以选择用递归或者循环两种方法。递归是一个函数内部的调用这个函数自身。循环则是通过设置计算的初始值以及终止条件，在一个范围内重复运算。比如，我们求累加1+2+3+…n，这个既可以用循环也可以用递归

 /*** 递归实现* */public Long addFrom1N(long n){return n <= 0 ? 0 : n + addFrom1N(n-1);}/*** 循环实现* */public long addForm1N_interative(long n){if(n <=0){return 0;}long result= 0;for (long i = 1; i < n; i++) {result +=i;}return result;}

• 如上案例实现，递归代码简洁，循环代码比较多，同样的在之前的文章二叉树实现原理在树的前序，中序，后序遍历的代码中，递归实现也明显比循环实现要简洁的多，所以我们尽量用递归来表达我们的算法思想。

• 递归的缺点：

  • 递归优点显著，由于是函数自身的调用，而函数调用有时间与空间的消耗：每一次调用都需要内存栈分配空间保存参数返回地址以及临时变量，而往栈里压入与弹出数据也需要时间，那就自然递归实现的效率比同等条件下循环要低下了
  • 另外递归中可能有很多计算是重复的，这个比较致命，对性能带来很大影响。
  • 除了效率，递归还有可能出现调用栈溢出问题。因为每个进程栈空间有限，当递归次数太多，超出栈容量，导致栈溢出。

案例分析：斐波那契数列

• 题目：写一个函数，输入n，求斐波那契（Fibonacci）数列的第n项。斐波那契数列的定义如下：

f(n) = f(n-1) + f(n-2) , n>1
f(n) = 0 , n=0
f(n) = 1 , n=1

斐波那契数列递归实现

• 记得谭浩强版本的C语言中讲解递归的时候就是用的斐波那契数列的案例，所以对这个问题非常的熟悉。看到之后自然就能提供如下代码：

 /*** f(n) = f(n-1) + f(n-2)* n > 2* n=1 : f(1) = 1* n=2 : f(2) = 1* f(3) = f(1) + f(2) = 1 + 1 = 2;*/public static Long getFibonacci(int n) {if (n <= 0L) {return 0L;}if (n == 1L || n == 2L) {return 1L;}return getFibonacci(n - 1) + getFibonacci(n - 2);}

• 教科书上只是为了讲解递归，这个案例正好比较合适，并不表示是最优解，其实以上方法是一种存在严重效率问题的解法，如下分析：
  • 我们求解f(10) 需要求解f(9)，f(8)，继而需要先求解f(8)，f(7)，…我们可以用树形结构来说明这种依赖求解关系：

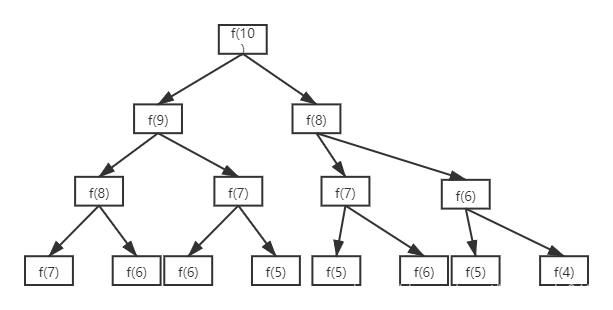
• 如上图中分解，树中很多节点是重复的，而且重复的节点数会随着n的增大指数级别的增大，我们可以用以上算法测试第100项的值，慢的你怀疑人生。

我认为的最优解：动态规划（循环实现）

• 改进方法并不复杂，上述代码中是因为大量重复计算，我们只要避免重复计算就行了。比如我们将已经计算好的数列保存到一个临时变量，下次计算直接查找前一次计算的结果，就无须重复计算之前的值。
• 例如我们从下往上算，根据f(0) 和f(1) 求f(2)， 继续f(1)，f(2) 求f(3)，依次类推得出第n项。很容易得出解。而且时间复杂度控制在O(n)
• 如下代码实现：

 /*** 动态规划求值* */public static Long getFibonacciGreat(int n) {if (n <= 0L) {return 0L;}if (n == 1L || n == 2L) {return 1L;}Long answer = 1L;Long last = 1L;Long nextLast = 1L;for (Long i = 0L; i < n - 2; i++) {answer = last + nextLast;nextLast = last;last = answer;}return answer;}

时间复杂度更优O（logn）但是复杂度过于高的解法

• 一般以上解法是最优解，但是如果在追求时间复杂度最优的算法场景下，我们有更快的O(logn)的算法。由于这种算法需要一个比较生僻的数学公式（离散数学没学好的代价），因此很少有人会去写这种算法，此处我们只介绍该算法，不递推数学公式（不会），如下：
• 先介绍数学公式如下：

$$\left[\begin{array}{cc}f(n)& f(n-1)\\ f(n-1)& f(n-2)\end{array}\right]={\left[\begin{array}{cc}1& 1\\ 1& 0\end{array}\right]}^{n-1}$$

• 如上数学公式可以用数学归纳法证明，有了这个公式我们只需要求如下矩阵的值，既可以的到f(n)的值，
  $${\left[\begin{array}{cc}1& 1\\ 1& 0\end{array}\right]}^{n-1}$$

• 那么我们只需要求，基础矩阵的乘方问题。如果只是简单的从0~n循环，n次方需要n次运算，那么时间复杂度还是O(n)，并不比之前的方法快，但是我们可以考虑乘方的如下性质
  $$\left[\begin{array}{cc}1& 1\\ 1& 0\end{array}\right]$$

• 情况一
  $$a^n=a^{n/2}\ast a^{n/2},n为偶数$$

• 情况二
  $$a^n=a^{(n-1)/2}\ast a^{(n-1)/2}\ast a,n为奇数$$

• 从上面公式我们看出，要求n次方，我们可以先求n/2次方，再把n/2次方平凡就可以。这可以用递归的思路来实现。

• 我们用如下方式实现，因为存在矩阵的计算，用代码实现比较繁琐，如下：

/*** 矩阵对象定义* @author liaojiamin* @Date:Created in 15:21 2021/3/16*/
public class Matrix2By2 {private long m_00;private long m_01;private long m_10;private long m_11;public Matrix2By2(){this.m_00 = 0;this.m_01 = 0;this.m_10 = 0;this.m_11 = 0;}public Matrix2By2(long m00, long m01, long m10, long m11){this.m_00 = m00;this.m_01 = m01;this.m_10 = m10;this.m_11 = m11;}public long getM_00() {return m_00;}public void setM_00(long m_00) {this.m_00 = m_00;}public long getM_01() {return m_01;}public void setM_01(long m_01) {this.m_01 = m_01;}public long getM_10() {return m_10;}public void setM_10(long m_10) {this.m_10 = m_10;}public long getM_11() {return m_11;}public void setM_11(long m_11) {this.m_11 = m_11;}
}*** 获取斐波那契数列* @author liaojiamin* @Date:Created in 12:06 2021/2/2*/
public class Fibonacci {/*** 矩阵乘法求值* */public static Matrix2By2 matrixMultiply(Matrix2By2 matrix1, Matrix2By2 matrix2){return new Matrix2By2(matrix1.getM_00()*matrix2.getM_00() + matrix1.getM_01()*matrix2.getM_10(),matrix1.getM_00()*matrix2.getM_01() + matrix1.getM_01()*matrix2.getM_11(),matrix1.getM_10()*matrix2.getM_00() + matrix1.getM_11()*matrix2.getM_10(),matrix1.getM_10()*matrix2.getM_01() + matrix1.getM_11()*matrix2.getM_11());}/*** 矩阵乘方实现* */public static Matrix2By2 matrixPower(int n){if( n<= 0){return new Matrix2By2();}Matrix2By2 matrix = new Matrix2By2();if(n==1){matrix = new Matrix2By2(1,1,1,0);}else if(n%2 == 0){matrix = matrixPower(n/2);matrix = matrixMultiply(matrix, matrix);}else if(n%2 == 1){matrix = matrixPower((n-1)/2);matrix = matrixMultiply(matrix, matrix);matrix = matrixMultiply(matrix, new Matrix2By2(1,1,1,0));}return matrix;}public static long getFibonacciBest(int n){if(n == 0){return 0;}if (n <= 0) {return 0;}if (n == 1) {return 1;}Matrix2By2 powerNminus2 = matrixPower(n-1);return powerNminus2.getM_00();}public static void main(String[] args) {System.out.println("-------------------------1");System.out.println(System.currentTimeMillis()/1000);System.out.println(getFibonacci(40));System.out.println(System.currentTimeMillis()/1000);System.out.println("-------------------------2");System.out.println(System.currentTimeMillis()/1000);System.out.println(getFibonacciGreat(40));System.out.println(System.currentTimeMillis()/1000);System.out.println("-------------------------3");System.out.println(System.currentTimeMillis()/1000);System.out.println(getFibonacciBest(40));System.out.println(System.currentTimeMillis()/1000);}
}

• 时间复杂度：设为f(n)，其中n 是矩阵的幂次。从上述代码中不难得出f(n) = f(n/2) + O(1) 。利用主定理，可以解得f(n) = O(${\log }^n$)

• 空间复杂度：每一次递归调用时新建了一个变量matrixPower(n/2)。由于代码需要执行${\log }_2^n$次，即递归深度是${\log }_2^n$ ，所以空间复杂度是O(${\log }^n$)

解法比较

• 用不同方法求解斐波那契数列的时间效率有很大区别。第一种基于递归的解法，时间复杂度效率低，时间开发中不可能会用
• 第二种将递归算法用循环实现，极大提高效率
• 第三种方法将斐波那契数列转换炒年糕矩阵n次方求解，少有这种算法出现，此处只是提出这种解法而已

变种题型

• 处理斐波那契数列这种问题，还有不少算法原理与斐波那契数列是一致的，例如：

• 题目：一只青蛙一次可以跳一个台阶，也可以跳两个台阶。求解青蛙跳上n个台阶有多少中跳法

• 分析

  • 最简单情况，如果总共只有一节台阶，只有一种解法，如果有两个台阶，有两种跳法，
  • 一般情况，n级台阶看出是n的函数，记f(n), 当 n> 2 时候，第一次条就有两种不同选择，
  • 第一种跳1级，此时后面的台阶的跳法等于f(n-1) ,那么总的跳法是 1 * f(n-1) = f(n -1)
  • 第二种跳2级，此时后面的台阶跳法等于f(n-2) ,那么总的跳法是 1*f(n-2) = f(n-2)
  • 所以n级台阶的不同跳法是 (n) = f(n-1) + f(n-2)，实际上就是斐波那契数列

上一篇：数据结构与算法–查找与排序另类用法
下一篇：数据结构与算法–位运算