数据结构与算法--查找与排序另类用法-旋转数组中的最小数字

查找与排序

查找

查找与排序都在程序设计中常被用到的算法。查找相对而言简单，一般都是顺序查找，二分查找，哈希表查找，和二叉排序树查找。其中二分查找是我必须熟悉的一种。
哈希表和二叉排序树主要点在于他的数据结构而不是算法。哈希表主要的优点是我们利用他能在O(1)的时间查找某个元素，是效率最高的查找方式。但是缺点是需要额外空间来实现哈希表
二叉排序树查找算法对应的数据结构是二叉搜索树（或者叫二叉查找树），之前我们已经着重讨论过这种数据结构原理以及自己的实现。

排序

排序比查找要复杂，例如经常选择一种排序算法的时候经常会对各种排序算法进行比较：插入排序，冒泡排序，归并排序，快速排序等不同算法的优劣。而这些都是必须掌握的排序算法，我们必须能从空间福再度，时间复杂度等方面去分析他们的优缺点。其中快速排序是重中之重。可见的几种排序算法在之前的章节中也用动图的方式给出来详细的解释，实现。

实际案例

快排是重要的排序算法，但是在具体场景下我们需要选择最优最合适的算法，例如下情况：
- 实现一个排序算法，实际复杂度，空间复杂度必须不超过O(n)，对公司所有员工年龄进行排序。
- 分析上题中，重点空间复杂度，实际复杂度O(n)
- 排序对象，员工年龄，我们假设员工都是100 岁以下，量级也不大，一个公司最多也就10万
- 这种情况，数组区间范围是固定的，而且基数不大最理想的排序算法是计数排序

另类用法：旋转数组中的最小数字

题目：将数组最开始的若干个元素搬到数组的末尾，我们称为数组的旋转。输入一个递增数组的旋转，输出旋转数组的最小元素，例如数组{3,4，1,5,1，2}是{1,2，3,4，5}的一个旋转，明显最小值是1，

分析

直观来看找最小值一次遍历就能搞定，时间复杂度O(n)，但是这个并没有利用这个数组的特性，已排序，旋转后两部分有序肯定有更优解
旋转后，两部分数组都有序，并且递增，必然有序部分后面大于前面
然后分界处必然是最小值的特点
由上部分分析我们自然想到二分查找寻找最小值。
流程如下：
- 定义指针min，max分别指向数组两端，按题意，第一个元素应该大于等于最后一个元素，因为旋转过。
- 接着找中间元素mid =（max+ min）/2, 如果中间元素大于min，则min到mid之间处于递增，则最小值必然在中间元素后面
- 此时我们将min指针移动到mid位置
- 同样如果中间元素mid 小于min，则表示最小值在mid或者mid的左边，
- 此时我们将max指针移动到mid位置
- 依次对min，max之间的数组部分进行如上流程，直到 max - min = 1 为止，此时最大，最小是相邻，则找出最小值
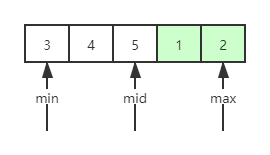
如下实际案例{3,4，5,1，2}，
- min指针指向第0个元素 3 ，max指向最后一个2，中间元素5
- 5 > 3，min移动到mid位置，也就是min指向5
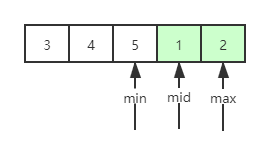
- 再次，中间元素变为1,1<5,此时，最小值在min右边
- 将max移动到mid位置，也就是max指向1 ，
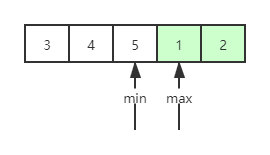
- 此时max - min = 1，得到最小值max位置。

在这里插入图片描述

代码实现

/*** @author liaojiamin* @Date:Created in 11:39 2021/3/16*/
public class FindRotateMin {public static int findMin(int[] array){if(array == null || array.length <= 0){return -1;}if(array.length == 1){return array[0];}if(array.length == 2){return array[0]> array[1] ? array[0] : array[1];}int index1 = 0;int index2 = array.length -1;int indexMin = index1;while (array[index1] >= array[index2]){if(index2 - index1 == 1){indexMin = index2;break;}indexMin = (index2 + index1)/2;if(array[indexMin] >= array[index1]){index1 = indexMin;}else if(array[indexMin] <= array[index1]){index2 = indexMin;}}return indexMin;}public static void main(String[] args) {int[] array = {3,4,5,0,1,2};System.out.println(array[findMin(array)]);}
}

问题：上述代码中我们每次判断都会有等于的情况，当index1， index2,两个相同的时候，并且他们中介的数字indexMin也相同，这个时候，我们符合第一个判断，将indexMin赋值给了index1，此时默认最小数字在后面，其实不一定对，如下反例
数组{1,0，1,1，1} 和数组{1,1，1,0，1} 都可以看成递增排序{0,1，1,1，1}的旋转，但是下图中最小值分别在左边和右边：

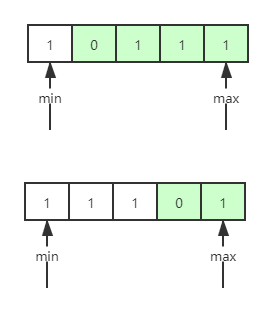
在这里插入图片描述

如上情况，首尾数字，中介位置数字都是1 ，但是却有两种不同的最小值位置，因此这种特殊情况：当两个指针数字以及中间数字都一样的时候，无法判断最小值的位置，我们不得不采取遍历的方式。
修改代码如下

/*** 二分排序另类用法* Created by jiamin5 on 2021/3/15.*/
public class FindRotateMin {public static int finMin(int[] array){if(array.length <= 0){return -1;}if(array.length == 1){return array[0];}if(array.length == 2){return array[1];}int index1 = 0;int index2 = array.length -1;int indexMin = index1;while (array[index1] >= array[index2]){if(index2 == index1 +1){indexMin = index2;break;}indexMin = (index1+index2)/2;if(array[index1] == array[index2] && array[indexMin] == array[index1]){return findMinList(array, index1, index2);}if(array[index1] <= array[indexMin]){index1 = indexMin;}else if(array[indexMin] <= array[index2]){index2 = indexMin;}}return array[indexMin];}public static int findMinList(int array[], int index1, int index2){int result = array[index1];for (int i = index1; i <= index2; i++){if(array[i] < result){result = array[i];}}return result;}public static void main(String[] args) {int[] array = {4,5,6,7,8,0,1,1,1,2,2,2,3,3,3,3,4,4};System.out.println(finMin(array));}
}