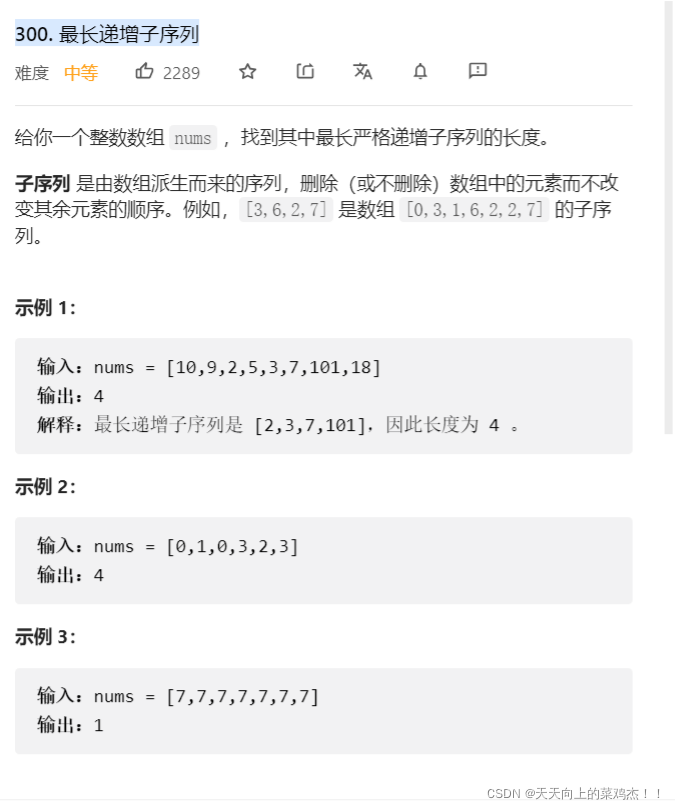
一:题目

二:上码

class Solution {
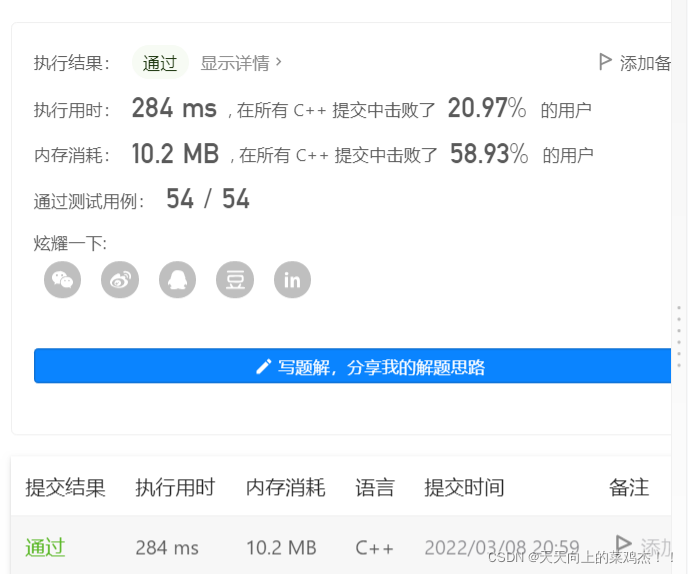
public:/**思路:1.分析题意:我们在求取答案的过程中;我们的结果是动态的;  如果从某个数有一个递增序列 但是在这个数的后面又有一个数又可以是递增的 而且可能还比起长 2.动态规划五步走1>:确定dp数组的含义以及下标的含义dp[i] 表示的是 i 之前的数 且包括i的 最长上升子序列长度这里就是 i 之前的数到最后下标会有一个递增序列 但是我们要取得是最长的  2>:确定dp数组的状态转移方程if(nums[i] > nums[j]) dp[i] = max(dp[j]+1,dp[i]);当出现nums[i] > nums[j] 的时候 我们就需要注意的是 那么dp[j]的值就需要改变了 因为后面又出现一个比其要大的值,所以我们需要跟当前的dp[i]进行比较从[0,i-1]的遍历过程中（也就是内循环）我们需要知道的是dp[i]是动态变化的eg: 0 1 2 3 4 5  6 6 7 8 9 2 3 10.... 当i为6的时候 nums[i] = 10  比前面的数都大,dp[i] = 1 //初始值j = 0  dp[i] = 2j = 1  dp[i] = max(dp[i],dp[j]+1) = 3//这里我们需要知道的是 dp[1] =2 dp[2] = 3 因为我们是从//前往后遍历的j= 2   dp[i] = max(dp[i],dp[j]+1) = 4//这里max中dp[6] = 3 但是dp[2] + 1 = 4j = 3  dp[i] = 5j= 4   dp[i] = max(dp[i],dp[j]+1) = 4//这里的dp[j=4] = 1  但是我们的dp[i] = 4的//这也就是回归到我们的dp[i]含义上了 也就是序列//[0,i]中的最长增长序列 3>:确定dp数组的初始化	无论哪个数都是14>:确定dp数组的遍历顺序我们的dp[i]是比较其前面的几个数的最大值的遍历i在外层  j在内层for(int i = 1; i < nums.size(); i++) {for(int j = 0; j < i; j++) {if(nums[i] > nums[j])dp[i] = max(dp[j]+1,dp[i]); //dp[i] 表示的是i之前且包括i的最大值}}5>:举例验证0 1 0 3 2 0   1   2   3   4 初始化   1   1   1   1   1i=1     1   2    1   1   1i=2     1   2    1   1   1i=3     1   2    1   3    1  //关于这里的3 我们需啊哟注意的是我们是遍历完[0,i-1]后取的最值i=4     1   2    1   3    3*/int lengthOfLIS(vector<int>& nums) {vector<int> dp(nums.size(),1);for (int i = 1; i < nums.size(); i++) {//这里我们先需要从1开始  因为我们的是要计算从[0,i-1]之前的最大值for (int j = 0; j < i; j++) {if(nums[i] > nums[j]) dp[i] = max(dp[i],dp[j]+1);}}int ans = 0;for(auto num: dp) {ans = max(ans,num);}return ans;}
};