| #include <iostream>
|
//
知树的前序遍历,后序遍历,怎么求中序遍历?
通过对同一棵二叉树三种遍历方式的分析,概括出由前序、中序或由中序、后序遍历结果快速还原二叉树的方法。
二叉树是最为常用的数据结构,它的实际应用非常广泛。二叉树的遍历方式有三种,前序遍历、中序遍历、后序遍历。先序遍历的顺序为:NLR,即先根结点,然后左子树、右子树;中序遍历顺序为:LNR先左子树,然后根结点、右子树;后序遍历顺序为:LRN先左子树、然后右子树、根结点。由前序和中序遍历、由中序和后序遍历序列可以唯一确定一棵二叉树,而由前序和后序遍历序列不能唯一确定一棵二叉树。
二叉排序树对二叉树作了进一步的限定:根结点的权值大于(或小于)左子树中所有结点的权值;根结点的权值小于(或大于)其右子树中所有结点的权值。
那么如何根据三种遍历序列之间的关系及二叉排序树来快速还原一棵二叉树?下面以二叉树的前序和中序遍历序列为基础,利用二叉排序树的性质,给出快速还原二叉树的方法。
1由给定前序和中序序列或中序和后序序列还原二叉树的方法
例:前序序列:ABDECFGH 中序序列:DEBACGFH (后序序列:EDBGHFCA)
(1)给中序序列中的每个结点从小到大、从左到右赋以权值,如下:
D(1)E(2)B(3)A(4)C(5)G(6)F(7)H(8)
(2)还原时读入的序列为前序序列,从左到右依次读入序列中的各个结点值和相应的权值;
(3)由读入的序列,根据第1)步中给定的权值按照二叉排序树的构造规则构造二叉排序树。第一个读入的结点为根结点,其他结点分别为左右子树中的结点。设根结点为TT,权值为NN,当前读入结点为SS,权值为MM,若MM
(4)将SS插入到TT的左子树或右子树的过程中,仍然遵循3)中的规则,直至左子树或右子树为空时止。
(5)读入序列结束时,二叉树还原成功。
6)对于由中序序列和后序序列还原二叉树是,读入的序列为后序序列,从右向左读入,构造规则同上。还原结果与上述结果完全一致。
2还原方法的确定依据
二叉树遍历过程中,在中序序列中,根结点的左子树中的所有结点都在根结点的左侧,根结点的右子树中的所有结点都在根结点的右侧,这个特点恰好与二叉排序树具有相同的性质;在读入序列时,前序序列则从左向右读,这恰好与遍历二叉树的顺序相同;后序序列从右向左读,则按照根结点、右子树、左子树的顺序还原。
(1)设二叉树共有N个结点(N为大于1的正整数),我们按照还原方法给中序序列中的这N个结点分别赋予权值1,2…N,设根结点的权值为M(1
(2)由二叉树的遍历规则可知,权值为1,2…M-1的结点为根结点的左子树中的结点,而权值为M+1,…N的结点为根结点的右子树中的结点。
(3)将这N个结点划分成3个子集AA=(1,2…M-1)BB=(M)CC=(M+1,…N),由于前序序列第一个读入的结点必定为二叉根的根结点,所以BB为根结点,AA集为左子树,CC集为右子树。
(4)同理不断读入前序序列中的结点,依次递归还原BB对应的左子树和CC对应的右子树,最后将三棵子树合并成以BB为根结点、AA的根结点为BB的左子树、CC的根结点为BB的右子树的一棵二叉排序树。
(5)同理可以得出,由中序序列和后序序还原二叉树的规则也成立。
(6)在还原过程中,读入序列的顺序也遵循也先根结点,后子树的规律。
3总结
在二叉树的一些应用中,如平衡二叉树、红黑树等,常常要观察二叉树的形态,对其进行判断并调整。根据遍历序列和二叉排序树的性质快速还原出二叉树对于研究相关的问题有很大的帮助。
上面可以得出前序扩展序列 ABD/E///C//FG//H
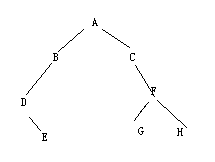
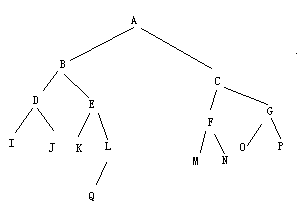
后序为 ED##B###G##HFCA
void PreCreate(Node* p)
{
if(line == end)
return;
if(line == “/”)
p = NULL;
else{
p = new NOde();
p->data = line;
PreCreate(p->Left);
PreCreate(p->Right);
}
}
本文转自博客园知识天地的博客,原文链接:二叉树的前序、中序、后序遍历与创建,如需转载请自行联系原博主。




![[CQOI2012]模拟工厂 题解(搜索+贪心)](http://pic.xiahunao.cn/[CQOI2012]模拟工厂 题解(搜索+贪心))














