目录
一、卷积神经网络
1、卷积神经的作用
2、LeNet
1)数据库准备——minst
2)模型·
二、关于卷积神经网络结构的一些术语定义
1、特征图(Feature map)
2、height(长度)、width(宽度)、Channel(通道)
3、卷积核(convolution kernel、filter)
4、步长(stride)
1)步长刚好使得卷积核遍历图像
2)步长不能使得卷积核遍历图像
问题1:原始图像有一些数据没有被卷积核训练怎么解决?
5、小结——原始图像大小、卷积核大小、步长核特征图像大小之间有什么关系
三、LeNet卷积神经网络结构
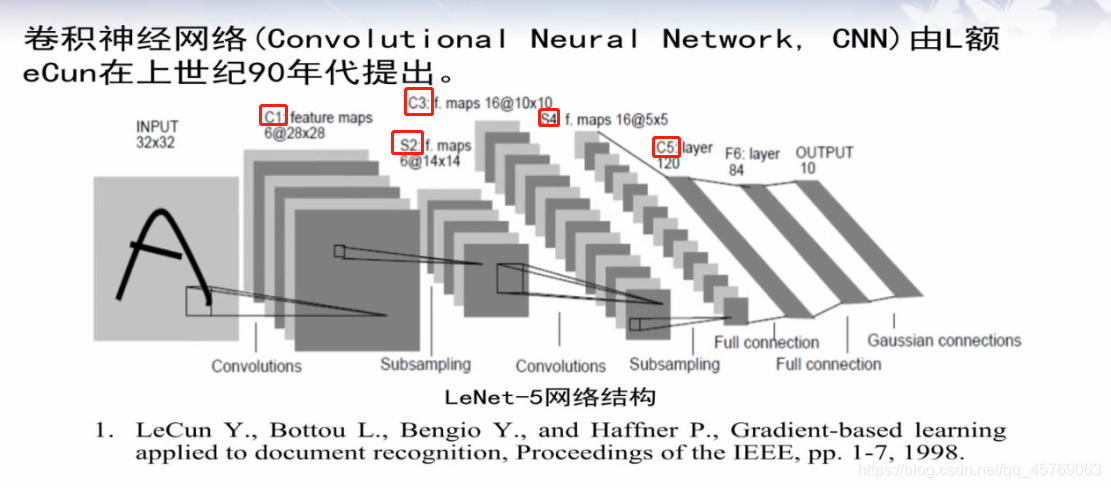
1、LeNet卷积神经网络结构模型
2、LeNet第一层卷积层 convolution
1)LeNet第一层卷积层模型
2) LeNet第一层卷积层待求参数个数
3)共享权重(weight sharing)
问题2:上图的神经网络和之前学习人工神经网络(常规神经网络)有什么区别?
2、LeNet第二层池化层 (subsampling)
问题3:卷积后进行后向传播时按照正常的BP即可,但是池化后的层进行进行后向传播到池化前的层呢?
3、LeNet第三层卷积层 (convolution)
4、全连接层(full connection)
1)全连接层的模型和定义
2)全连接层的待定参数
5、输出层(OUTPUT)
1)目标函数E
问题4:什么是SoftMax?
6、LeNet卷积神经网络结构参数计算
四、TENSORFLOW实现LeNet-5
图 LeNet卷积神经网络结构前接:《机器学习——深度学习之数据库和自编码器》
一、卷积神经网络
1、卷积神经的作用
由手工设计卷积核转换为自动学习卷积核
卷积公式有很多:如傅里叶变换、小波变换等
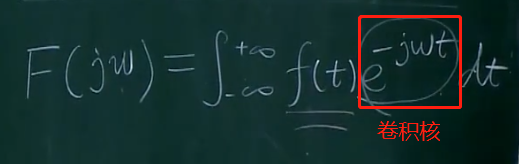
卷积核主要的作用就是将元素先乘再加(积分的本质就是加)
2、LeNet
1)数据库准备——minst

2)模型·
二、关于卷积神经网络结构的一些术语定义
1、特征图(Feature map)
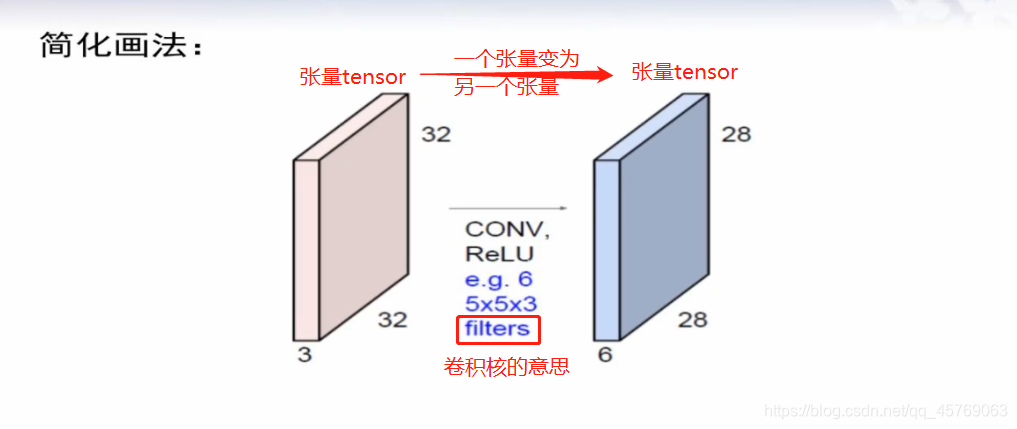
原图像经过卷积核作用得到的图像称为特征图,如图 LeNet卷积神经网络结构所示
2、height(长度)、width(宽度)、Channel(通道)
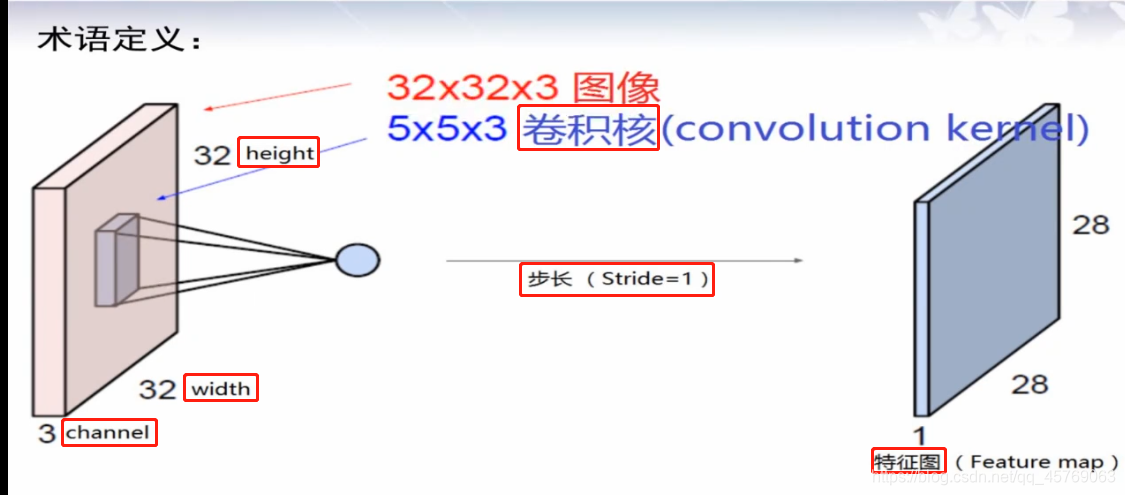
height和width定义了图像(我们叫做tensor张量)的大小,长宽
channel定义了图像的颜色,如果是彩色channel=3,表示rgb三原色,如果是黑白二值图,则channel=1
如图 LeNet卷积神经网络结构,图像的大小为32*32,具体的单位应该是像素,颜色为彩色因为channel=3
3、卷积核(convolution kernel、filter)
如图 LeNet卷积神经网络结构,卷积核的大小为5*5,也是彩色,这里的卷积核可以理解为是一个小的图像,活动范围是32*32*3的长方体内,按照一定的规律,卷积核可以对图像进行扫描
以二值图为例进行说明
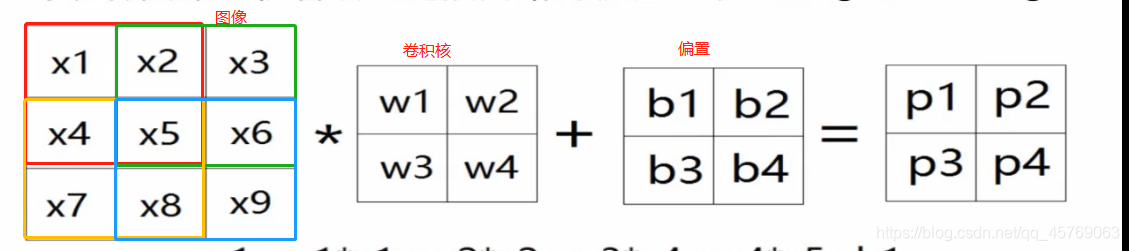
二值图像大小为3*3*1,卷积核为2*2*1,用卷积核从左上角开始进行扫描,按照一行一行进行,将卷积核与扫描重合的图像对应的参数进行相乘然后再相加,得到卷积核在该位置的卷积数,如上图的Pi,上图还有一个偏置(大家可以按照人工神经网络的模型去理解这里的b),上图图像处每一个颜色框代表卷积核扫描的一个地方,扫描的地方就是在进行卷积,最后会得到如下图所示的公式。每移动一个地方,就对应得到了特征图的一个参数
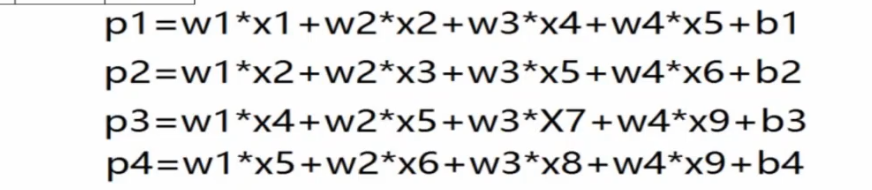
那么卷积核究竟该按照什么规律去移动呢,这就涉及到了步长这个概念。
4、步长(stride)
步长顾名思义就是每一步移动的长度,这里的步长控制的是卷积核扫描的长度,如stride=【1,1】表示的是卷积核每一步向右移动一个单位长度,换行时也是在纵向上移动一个单位长度
如下图移动的步长就是【1,1】

1)步长刚好使得卷积核遍历图像
图像5*5*3
卷积核2*2*3
步长【1,1】
特征图像4*4*1
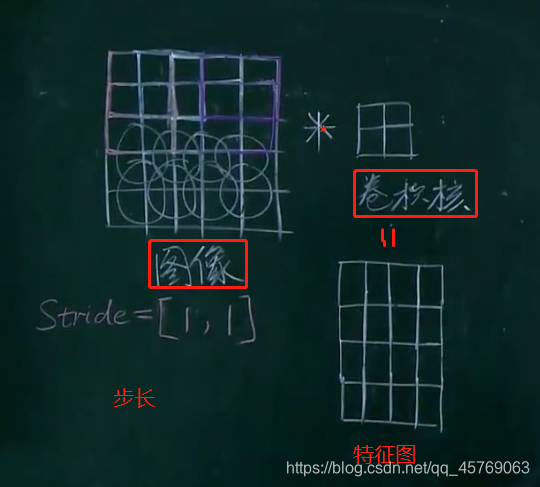
2)步长不能使得卷积核遍历图像
图像5*5*3
卷积核2*2*3
步长【2,2】
特征图像2*2*1

由上图可知原始图像没有被卷积核全部遍历(上图红色框图部分)
问题1:原始图像有一些数据没有被卷积核训练怎么解决?
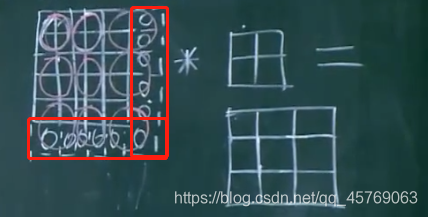
答:补零法(zero-padding)
如下图所示将原始图像两边用零补齐,使得原始图像的原有特征能够全部被卷积核所卷积
最多补零数为四周均不加一层零
5、小结——原始图像大小、卷积核大小、步长核特征图像大小之间有什么关系
假设有:
原始图像大小:M*N*3
卷积核大小:m*n*3
步长:(u,v)
特征图像大小:K*L*1
则有:
K<=(M-m)/u + 1
L<=(N-n)/v + 1

三、LeNet卷积神经网络结构
1、LeNet卷积神经网络结构模型
分为5层
第一层卷积层——convolution
第二层池化层——subsampling
第三层卷积层——convolution
第四层池化层——subsampling
第五层:
全连接层——full connection
全连接层——full connection

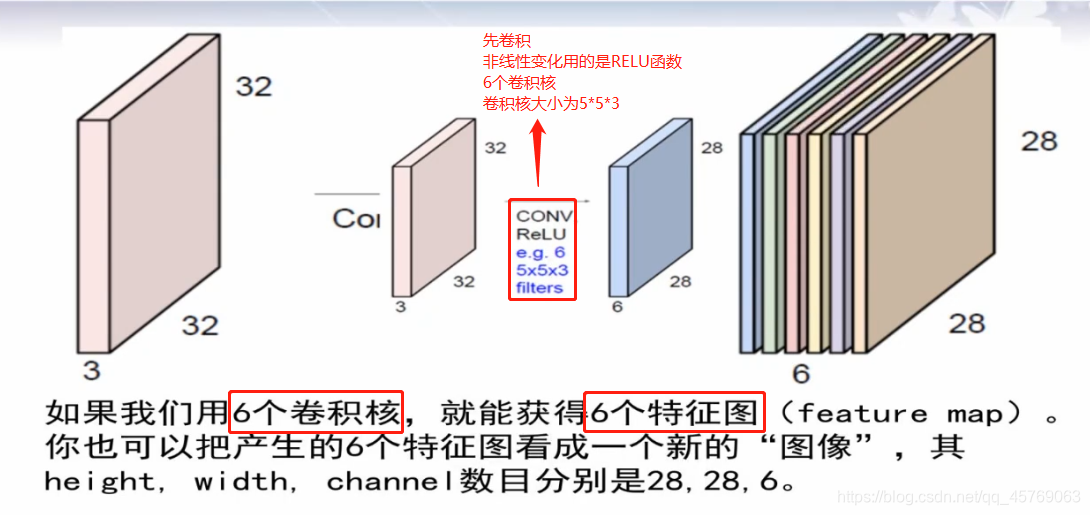
2、LeNet第一层卷积层 convolution
32*32*3——28*28*6
1)LeNet第一层卷积层模型
特征图的个数和卷积核的个数是一样的,具体点就是特征图像的channel的值和卷积核的个数相同
注意:非线性转换不会改变图像的大小,只是对图像的每一个特征进行非线性变化,最后得到的大小和非线性变换前是一样的
2) LeNet第一层卷积层待求参数个数
首先是一个卷积核中的参数个数为:
m=5*5*3 = 75
在LeNet中有6个卷积核则:6m = 75*6=450
注意:以上的参数的个数没有偏置,一般一个卷积核是会自带一个偏置的,即b,所以有卷积核参数为:
6*(m+1)=6*76=456,有没有偏置有自己定义
实际上b是一个和卷积核大小一样的矩阵,但是一般将其作为一个参数来进行处理

其实偏置的形式可以通过原始图像大小、卷积核大小、步长核特征图像大小之间的关系来进行确定的,先计算出特征图像的大小(K,L),这样的话偏置的形式和特征图像的大小是一样的
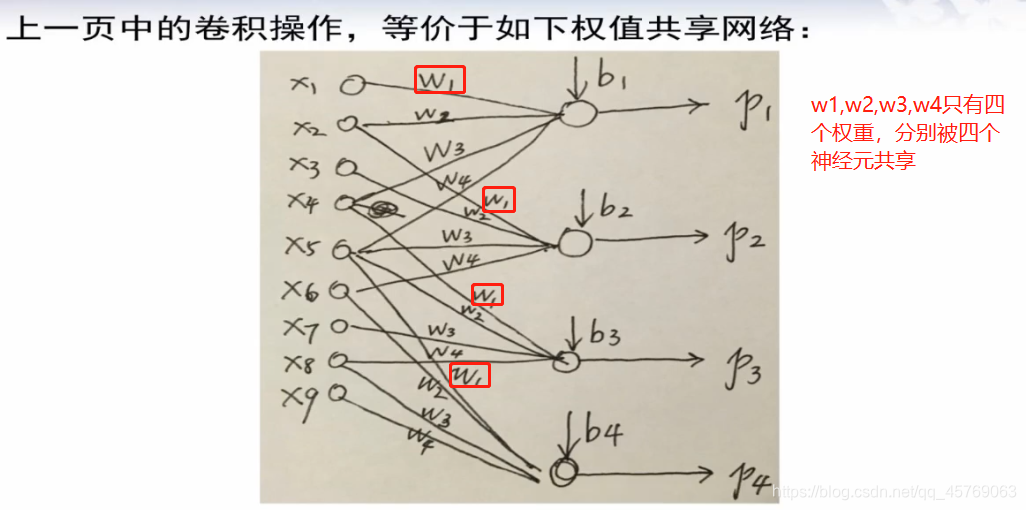
3)共享权重(weight sharing)
共享权重就是同一个权重被不同的神经元之间所共享,或者说不同的神经元之间的权重有相同的
这里可以用类似于神经网络的方法来表示以下图的关系

问题2:上图的神经网络和之前学习人工神经网络(常规神经网络)有什么区别?
答:两个区别:
不本质区别:上图中,并不是所有的输入神经元和下一层的神经元都有权重,即只有部分神经元之间进行了连线,而常规的神经网络是每个神经元之间都有需要连线的即有权重,但是这个区别我们把没有连线之间神经元的权重看成是0即可,因此此为不本质区别
本质区别:上图神经网络的权重是共享的

2、LeNet第二层池化层 (subsampling)
28*28*6——14*14*6
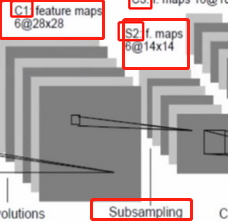
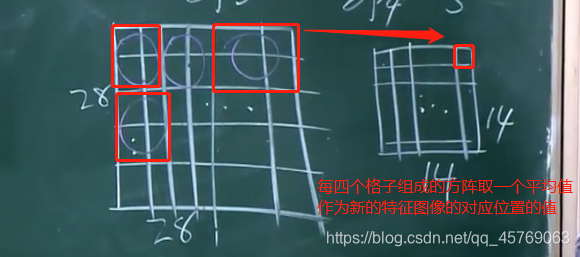
做的事情就是降维采样,即将第一层得到的特征图像中的大小分成若干份,将这若干份每一份中的参数特征取一个平均值,作为这一份的新的参数,这个过程叫做池化,最后组合成一个新的特征图像
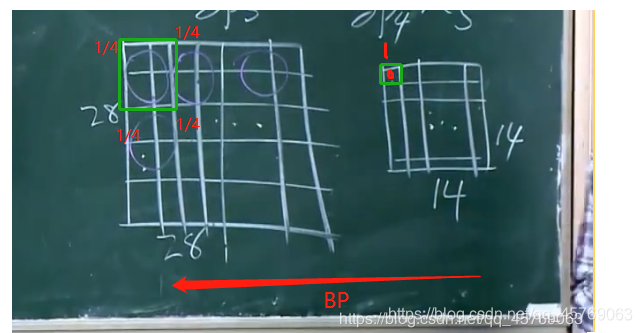
问题3:卷积后进行后向传播时按照正常的BP即可,但是池化后的层进行进行后向传播到池化前的层呢?
答:因为池化的过程就是将4个格子取了一个平均值作为池化后的一个格子,那当我们进行后向传播时,我们将池化后的层的一个格子的1/4梯度作为池化前的4个格子的每一个格子的梯度即可
3、LeNet第三层卷积层 (convolution)
14*14*6——10*10*16
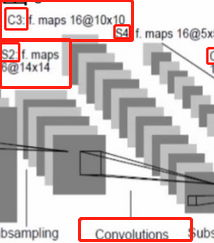

利用和图像同channel的卷积核去卷积图像得到的特征图像的channel=1,这里用了16个和图像同channel的卷积核去卷积图像,因此得到的特征图像的channel=16,至于为什么是10,可以通过《原始图像大小、卷积核大小、步长核特征图像大小之间的共关系》来进行求得,(14-5)/1 + 1 = 10
4、全连接层(full connection)
这一部分按照人工神经网络去理解就好了
1)全连接层的模型和定义
在全连接前之前还有一层池化层,这里不再赘述,与第一层的池化层原理一样
全连接层其实即使常规的神经网络层了,和卷积层的区别就是:
不本质区别:上图中,并不是所有的输入神经元和下一层的神经元都有权重,即只有部分神经元之间进行了连线,而常规的神经网络是每个神经元之间都有需要连线的即有权重,但是这个区别我们把没有连线之间神经元的权重看成是0即可,因此此为不本质区别
本质区别:上图神经网络的权重是共享的
说简单一点就是:全连接层的相邻两层的神经元是全部都会相互连接的,且权重不会共享,每一对神经元之间的权重是独立的
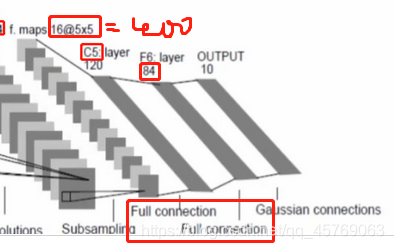
2)全连接层的待定参数
由上图可知,第一层全连接层的输入为池化层的输出,其特征参数为:5*5*16=400,也就是说全连接层的输入层的神经元个数为400个,输出层神经元个数为120,则有参数(400+1)*120个,其中加1是因为还有一个偏置;
同理·可得第二层全连接层的输入层即使第一层全连接层的输出,有神经元个数120个,输出层有神经元个数80,则参数的个数为:(120+1)*84
还有最后一层就是全连接层到输出层(output),易得参数个数为:(84+1)*10

5、输出层(OUTPUT)
这一层主要就是将前面通过卷积、池化、全连接得到的预测值输出,在LeNet卷积神经网络中,使用的数据库是Mnist库,共有10类,因此输出层为10个神经元。属于哪一类那么哪一类神经元的输出值为1,其余9个神经元的输出为0

这样就回到我们熟悉的人工神经网络问题上去了!
具体可见:《【机器学习】神经网络BP理论与python实例系列》
但是需要注意的是:目标函数发生了改变
1)目标函数E
交叉熵的方式
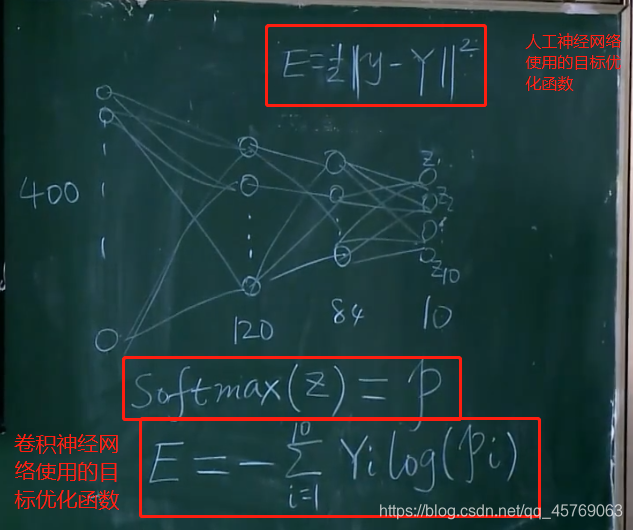
问题4:什么是SoftMax?
答:可见文章:《小白都能看懂的softmax详解》
6、LeNet卷积神经网络结构参数计算

注:计算速度取决于卷积层(乘法多)——运行速度,参数个数取决于全连接层——存储空间
四、TENSORFLOW实现LeNet-5
用户只需要编写前向计算就可以,后向传播是tensorflow包自动计算的,并且tensorflow的数据和神经网络的描述是分开的,先是对神经网络进行描述,然后再将数据参数带入到神经网络中进行训练测试等。




主要参数详述)



—— xyz_attrib_to_object_model_3d)

——AlexNet卷积神经网络结构)


的使用)


—— calibrate_sheet_of_light_calplate.hdev)






