我貌似和所有的数据结构都有些误会。。。。。。
在处理一些修改查询问题的时候,我们可以利用分治的思想,比如说把一个线性的数据不断分成一棵二叉树,也就是我们所说的线段树,这样我们就可以在logn的时限里做到修改和查询。同理我们也可以把数据分成一个只有两层的树(算上根节点三层),每个节点分成sqrt(该节点大小)个节点,这就是我们所说的分块了。
这里我们主要讲解分块的思想:
话不多说先上一张图:
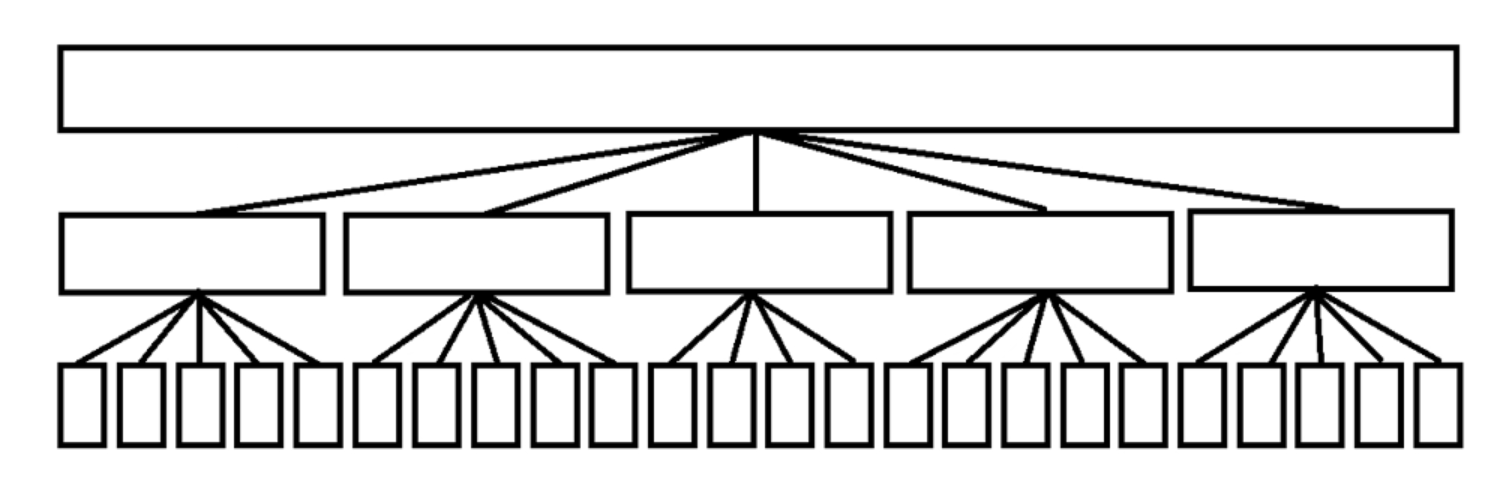
如图,我们这就是一个分好块的结构。
那么,这个结构有个什么用呢?很明显,我们可以用它维护单点修改与查询,区间的修改,查询。。。
看上去有些眼熟,是不是,想起来了些什么?
没错,就是线段树那几个操作。那么现在我们继续,可以发现分块的修改和查询操作都是O(sqrt(n))的。那还要分块有个什么用??
我们先来看这么一道题:
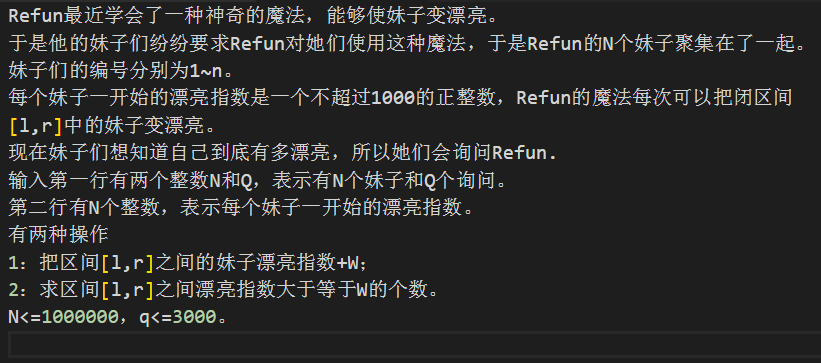
我们刚开始看的时候可能觉得可以用数据结构实现,什么线段树主席树平衡树都可以想一想,不过一会你就会发现,它们都不可行,过了一会,你会发现有一种线段树套平衡树的方法或许可做,只不过代码复杂度很高,而且估计要调不短的时间吧。这个时候就是分块出场的时候了。
为什么这个题不能通过线段树实现,原因就在于第二个操作过于烦人,线段树维护的区间信息无法找出单点的,如果要查找一个区间中的所有点,无法得到一个让人满意的复杂度。那么为什么分块就可以令人满意了呢??
首先我们说明几个接下来经常会说的名词:
整块:查询范围内完全包括的块,也就是范围内第二层的块。
零散块:查询范围内除了整块其他的部分,是第三层的块,也就是一个一个的点。
接着声明几个变量:

那么我们再修改的时候,对于区间内所有的整块,我们O(1)的打上加法标记即可。
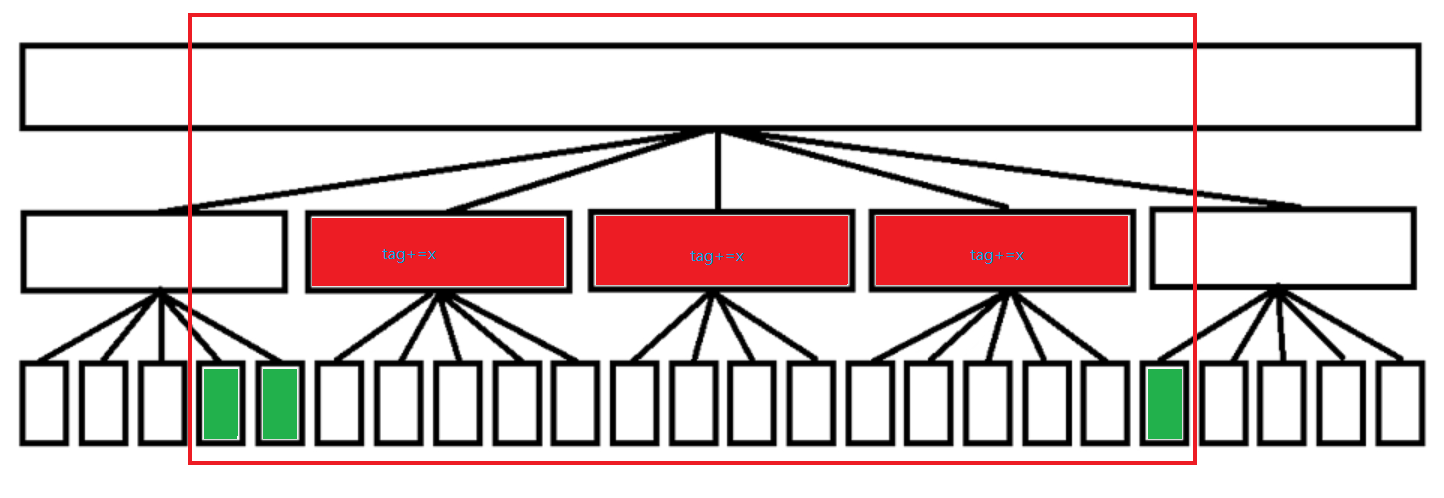
那么对于所有的零散块呢?
我们发现,我们最多有两个部分的零散块,其中每个部分里最多有不超过sqrt(n)个点,我们直接暴力枚举下标修改即可,那么整个修改操作的复杂度就是O(sqrt(n));
那么我们再查询的时候,对于每个整块,我们可以知道它是完全有序的,所以我们可以直接二分查找返回。对于零散块,我们仍然选择暴力枚举,那么查询操作的复杂度就是O(sqrt(nlogn))。
所以整个操作我们就可以在O(qsqrt(nlogn))的复杂度内完成了。
笔者秉承懂了算法不看模板的法则,自己手动实现了一下这个题目。接下来分块讲述一下代码的意义:
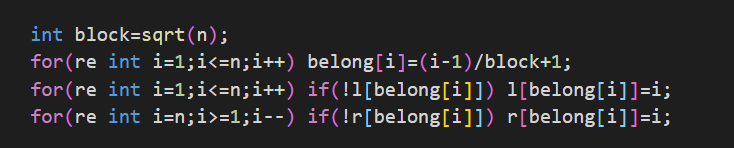
这一部分就是预处理并且分块的部分,和块的左右区间的处理。
然后在你的分块主体开始之前,必须要有的一条语句:

这条语句就是先把b数组的每一个块中的数据排好序,这样要不然很有可能找的时候由于每一块的b数组还没有排序导致查找错误。
然后就是分块的主体部分,我们分成修改和查询分别看一下:
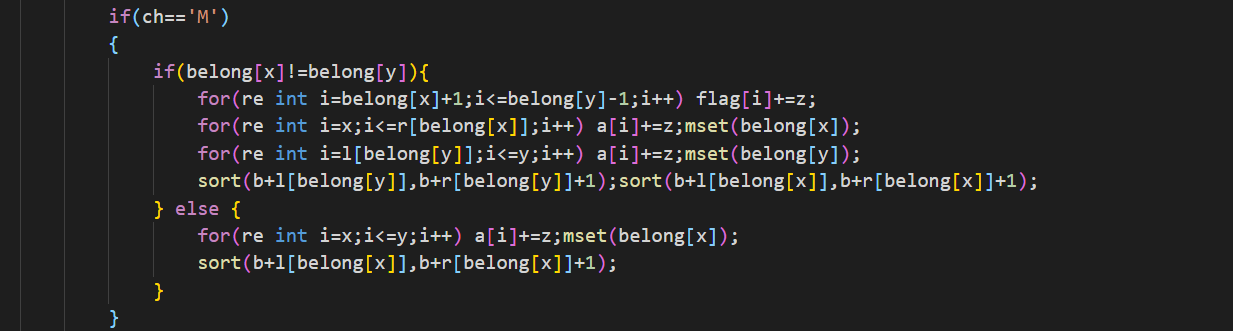
这个就是修改操作。要注意的是,在读入的x和y点属于同一个块的时候我们要特殊操作。
如果不在同一个块里,我们就遍历包含的所有整块,打上标记。然后对于左右那两个零散块,我们直接枚举就可以了。为什么用的是a数组而不是b数组?因为b数组在排完序之后下标代表的意义是数的大小顺序,而不是我们一开始读入的顺序,不能直接修改b数组。还有一个就是,这里笔者为了打上去方便,修改b数组的时候用了sort,这样我们的复杂度就增加了一个sqrt(logn)但是我们使用归并重构零散块的话还是可以达到sqrt(n)的。对于 在同一个块里的,我们也是直接暴力枚举就可以了。
为什么这些零散块可以暴力枚举,复杂度不会很高么?不会的,在修改每一个零散块的时候,我们最多也就修改sqrt(n)个点,所以并不会有特别高的额复杂度。
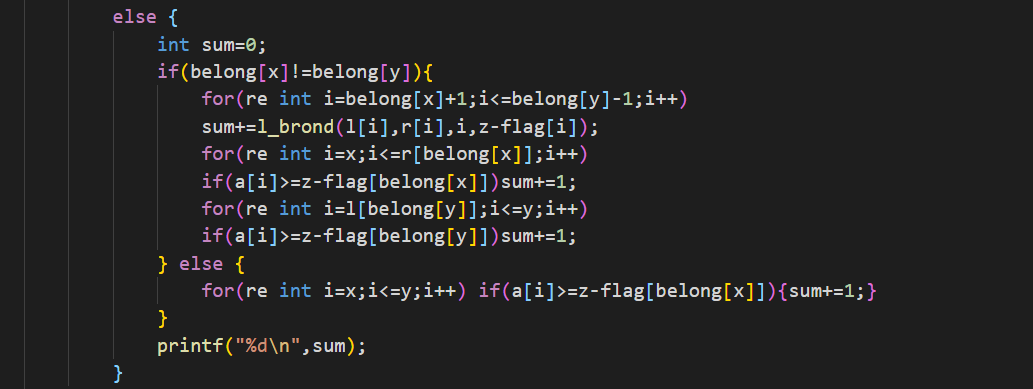
这个是查询操作,怎么查找刚才都已经说过了,同样零散块我们就暴力枚举即可。
那么这道题就这么完成了。
纯粹让你用分块完成的题目比较少,但是我们可以用这东西水一水分,毕竟这玩意比线段树什么的好写多了。








![BZOJ2333 [SCOI2011]棘手的操作 【离线 + 线段树】](http://pic.xiahunao.cn/BZOJ2333 [SCOI2011]棘手的操作 【离线 + 线段树】)










