包围体是一个简单的几何空间,里面包含着复杂形状的物体。为物体添加包围体的目的是快速的进行碰撞检测或者进行精确的碰撞检测之前进行过滤(即当包围体碰撞,才进行精确碰撞检测和处理)。包围体类型包括球体、轴对齐包围盒(AABB)、有向包围盒(OBB)、8-DOP以及凸壳。如图1所示。
图1 依次是球体、AABB、OBB
可以看到图1是3D包围体,在2D包围体如图2所示:
图2 依次是球体、AABB、OBB
OBB
方向包围盒(Oriented bounding box),简称OBB。方向包围盒类似于AABB,但是具有方向性、可以旋转,AABB不能旋转。如图3所示。
图3 矩形和矩形投影检测的四条轴
要计算两个OBB是否碰撞,只需要计算他们在图3上的4个坐标轴上的投影是否都发生重叠,如果是,则两多边形有接触。这也可以扩展到任意多边形,如图4所示。
图4 矩形和三角形投影检测的五条轴
投影轴来自于多边形自身边的垂线。
判定方式:两个多边形在所有轴上的投影都发生重叠,则判定为碰撞;否则,没有发生碰撞。
OBB存在多种的表达方式,这里使用最常用的一种:一个中心点、2个矩形的边长、两个旋转轴(该轴垂直于多边形自身的边,用于投影计算)。代码如下所示:
(function (window) {var OBB = function (centerPoint, width, height, rotation) {this.centerPoint = centerPoint;this.extents = [width / 2, height / 2];this.axes = [new Vector2(Math.cos(rotation), Math.sin(rotation)), new Vector2(-1 * Math.sin(rotation), Math.cos(rotation))];this._width = width;this._height = height;this._rotation = rotation;}window.OBB = OBB;
})(window);
其所依赖的Vector2这个类如下所示:
(function (window) {Vector2 = function (x, y) {this.x = x || 0;this.y = y || 0;};Vector2.prototype = {sub: function (v) {return new Vector2(this.x - v.x, this.y - v.y)},dot: function (v) {return this.x * v.x + this.y * v.y;}};window.Vector2 = Vector2;
} (window))
然后基于这个数据结构,进行OBB之间的相交测试。为OBB扩展一个方法,即或者在任意轴上的投影半径:
OBB.prototype = {getProjectionRadius: function (axis) {returnthis.extents[0] * Math.abs(axis.dot(this.axes[0])) + this.extents[1] * Math.abs(axis.dot(this.axes[1]));}
}
这里你可能需要读者了解Vector2.dot的几何意义:若b为单位矢量,则a与b的点积即为a在方向b的投影。
有了这些,就可以进行相交检测。由上面的判定方式,可以得出,两个矩形之间的碰撞检测需要判断四次(每个投影轴一次)。完整检测代码如下所示:
(function (window) {var CollisionDetector = {detectorOBBvsOBB: function (OBB1, OBB2) {var nv = OBB1.centerPoint.sub(OBB2.centerPoint);var axisA1 = OBB1.axes[0];if (OBB1.getProjectionRadius(axisA1) + OBB2.getProjectionRadius(axisA1) <= Math.abs(nv.dot(axisA1))) return false;var axisA2 = OBB1.axes[1];if (OBB1.getProjectionRadius(axisA2) + OBB2.getProjectionRadius(axisA2) <= Math.abs(nv.dot(axisA2))) return false;var axisB1 = OBB2.axes[0];if (OBB1.getProjectionRadius(axisB1) + OBB2.getProjectionRadius(axisB1) <= Math.abs(nv.dot(axisB1))) return false;var axisB2 = OBB2.axes[1];if (OBB1.getProjectionRadius(axisB2) + OBB2.getProjectionRadius(axisB2) <= Math.abs(nv.dot(axisB2))) return false;return true;}}window.CollisionDetector = CollisionDetector;
})(window)
这里拿两个OBB的中心点连线在坐标轴上的投影长度和两个矩形投影半径之和进行对比,如果半径之后都小于或者等于中心连线之后才判定为碰撞,否则判定为分离状态。
怎样判断平面上一个矩形和一个圆形是否有重叠?
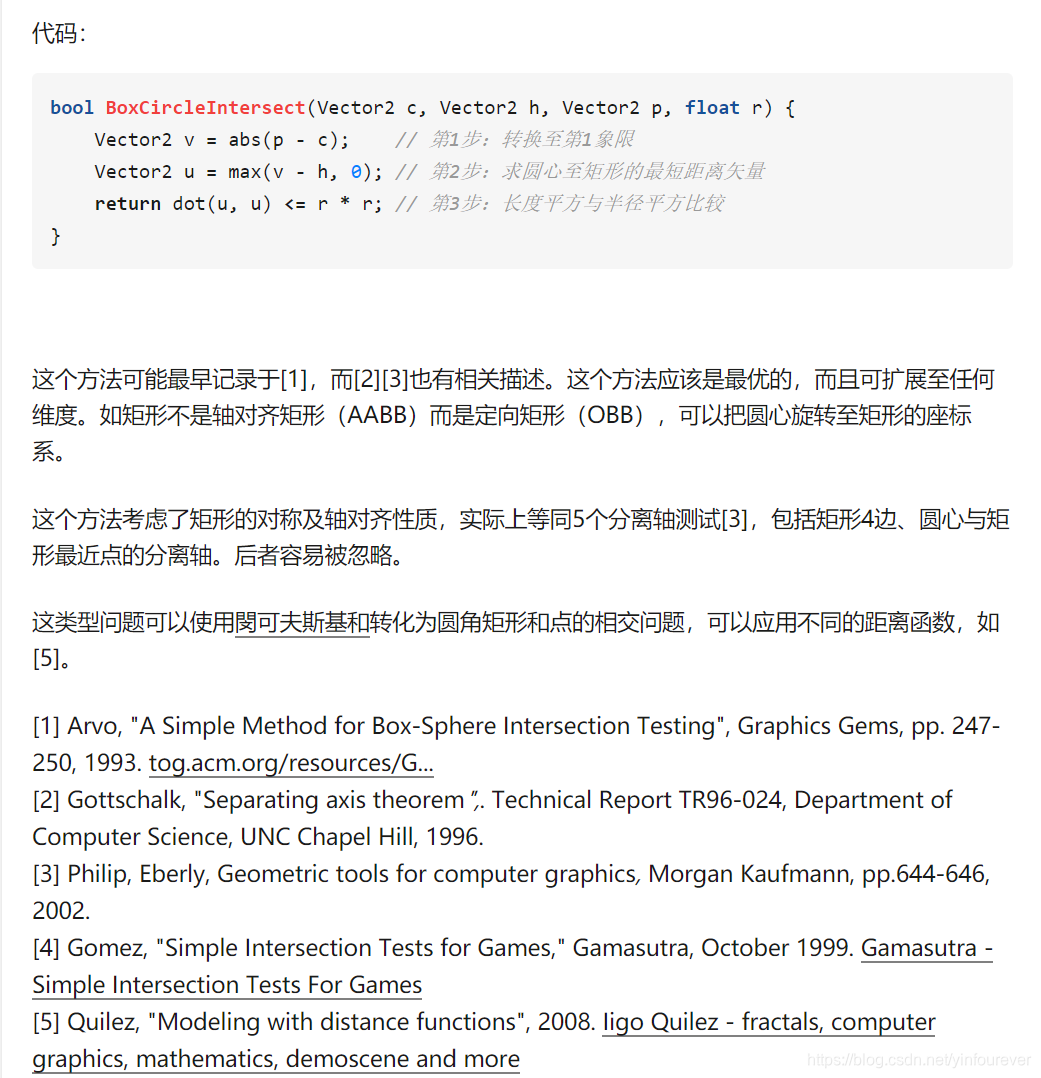
设c为矩形中心,h为矩形半長,p为圆心,r为半径。
计算方法是先找到矩形上离圆形最短距离u,然后再比较u是否小于圆形的半径r
1. 首先利用绝对值把 p - c 转移到第一象限,下图显示不同象限的圆心也能映射至第一象限,这不影响相交测试的结果:
2. 然后,把 v 减去 h,负数的分量设置为0,就得到圆心与矩形最短距离的矢量 u。下图展示了4种情况,红色的u是结果。
3. 最后要比较 u 和 r 的长度,若距离少于 r,则两者相交。可以只求 u 的长度平方是否小于 r 的平方。
转自知乎https://www.zhihu.com/question/24251545
方向包圍盒碰撞檢測
https://www.cnblogs.com/iamzhanglei/archive/2012/06/07/2539751.html
射线与平面的相交检测(Ray-Plane intersection test)
https://www.cnblogs.com/graphics/archive/2009/10/17/1585281.html
判断点是否在三角形内
https://www.cnblogs.com/graphics/archive/2010/08/05/1793393.html
射线和三角形的相交检测(ray triangle intersection test)
https://www.cnblogs.com/graphics/archive/2010/08/09/1795348.html
)
)




)










)

 Job System总览和多线程)