本文是一些关于齐次坐标知识的整合。

https://www.sohu.com/a/258317807_100007727

http://www.songho.ca/math/homogeneous/homogeneous.html

https://blog.csdn.net/VenoBling/article/details/87794400

https://www.cnblogs.com/csyisong/archive/2008/12/09/1351372.htm

在涉及到计算机视觉的几何问题中，我们经常看到齐次坐标这个术语。本文介绍一下究竟为什么要用齐次坐标？使用齐次坐标到底有什么好处？

什么是齐次坐标？

简单的说：齐次坐标就是在原有坐标上加上一个维度：

 

使用齐次坐标有什么优势？

齐次坐标的使用能够大大简化在三维空间中的点线面表达方式和旋转平移等操作，具体分如下几点进行说明。

1. 能非常方便的表达点在直线或平面上

在2D平面上，一条直线 l 可以用方程 ax + by + c = 0 来表示，该直线用向量表示的话一般记做

我们知道点p = (x, y)在直线 l 上的充分必要条件是 ax + by + c = 0 如果使用齐次坐标的话，点p的齐次坐标就是

p'=(x, y, 1)

那么 ax + by + c = 0 就可以用两个向量的内积（点乘）来表示：

因此，点p在直线l上的充分必要条件就是 直线l 与p的齐次坐标p'的内积：

是不是很方便呢！

同理，我们知道 三维空间的一个平面A可以用方程 ax + by + cz + d = 0 来表示，三维空间的一个点P=(x, y, z) 的齐次坐标 P'=(x, y, z, 1)，类似的，点P在空间平面A上可以用两个向量的内积来表示，如下：

因此，点P在平面A上的充分必要条件就是平面A 向量与P的齐次坐标P'的内积（点乘）：

2. 方便表达直线与直线，平面与平面的交点

先给出结论，后面再具体解释：

结论：在齐次坐标下，可以用两个点 p, q 的齐次坐标叉乘结果来表达一条直线 l，也就是

l = p x q

也可以使用两条直线 l, m 的叉乘表示他们的交点 x

x = l x m

见下面示例图。

之所以可以这么简洁的表示交点是因为采用了齐次坐标的表示方式。那么这是为什么呢？先介绍一下叉乘（也称叉积、外积）的概念：

两个向量 a和b 的叉乘仅在三维空间中有定义，写作 a x b.  a x b 是与向量 a, b都垂直的向量，其方向通过右手定则（见下图）决定。

其模长等于以两个向量为边的平行四边形的面积（见下图）。

叉乘可以定义为：其中 θ表示a, b的夹角（0°到180°之间），||a||, ||b||是向量a, b的模长,n则是一个与向量a, b所构成的平面垂直的单位向量.

根据叉乘定义：向量自身叉乘结果为0，因为夹角为0。也就是说三维向量 a x a =0, b x b = 0而点乘（也称点积，内积）的定义是

a * b = ||a||* ||b|| *cos(θ)

根据定义：如果两个向量垂直，cos(θ) = 0，点积也为0。好了，经过上面点乘和叉乘定义的铺垫。下面来推导一下上面的结论：

为什么两条直线 l, m 的叉乘 l x m 等于它们的交点 p，也就是 p = l x m？

原因如下：首先，根据前面叉乘的定义，l x m 的结果向量（记为 p = l x m） 与 l 和 m都垂直，根据点乘的定义，垂直的向量之间的点积为0，因此可以得到：

因此，根据前面点在直线上的结论，可以看到p既在直线l 上又在直线m上，所以 p = l x m 是两条直线的交点。此处 p 是齐次坐标。同样的，可以证明，两点p, q 的叉乘 可以表示 过两点的直线l，即 l = p x q。

3.能够区分一个向量和一个点

(1)从普通坐标转换成齐次坐标时

如果(x,y,z)是个点，则变为(x,y,z,1);

如果(x,y,z)是个向量，则变为(x,y,z,0)

(2)从齐次坐标转换成普通坐标时

如果是(x,y,z,1)，则知道它是个点，变成(x,y,z);

如果是(x,y,z,0)，则知道它是个向量，仍然变成(x,y,z)

具体解释见：http://www.cnblogs.com/csyisong/archive/2008/12/09/1351372.html

4.能够表达无穷远

每个人都熟悉的知识：在欧几里得空间，一个平面的两条平行直线永不相交。但在投影空间却不是这样的。

例如，图里的铁轨随着远离视线而变得越来越窄，最终在无限远处相交于一点 

欧几里得和笛卡尔空间描述3D或2D几何结构的方式不适用于投影空间（事实上欧几里得空间是投影空间的一个子集）
在笛卡尔坐标系里用（x,y）来表示一个点，当这个点变得无限远的时候怎么表示呢？可以用（∞，∞）来表示。这样的点在欧几里得空间没有意义。两条平行线在投影空间的无限远处相交，但在欧几里得空间永远也不相交。数学家们已经发现了解决这个问题的方法。
解决方案：齐次坐标
奥古斯特·斐迪南·莫比乌斯（ August Ferdinand Möbius,1790-1868,德国数学家）引入了齐次坐标，用来在投影空间计算几何图形。齐次坐标是一种用N+1个数字来表示N维坐标系的方法。
在现有的2D坐标里增加一个w，就形成了2维的齐次坐标。因此，笛卡尔坐标（X,Y）就变成了（x,y,w）。而笛卡尔坐标里的X和Y与齐次坐标里x和y的对应关系可以这样来表示：X=x/w, Y=y/w
例如，（1,2）变成了（1,2,1）。当（1,2）移向无穷远（∞，∞），即（1,2,0）。因为（1/0,2/0）≈（∞，∞）。所以无穷远的点就可以不用符号“∞”来表示了。
为什么叫“齐次的”？
前边已经提到过，将齐次坐标（x,y,w）的两个分量x,y除以w就可以得到笛卡尔坐标(x/w,y/w)。一个重要的事实：
（1,2,3）=>（1/3,2/3），（2,4,6）=>（2/6,4/6）···（1a,2a,3a）=>（1/3,2/3）
这些齐次坐标都对应相同的笛卡尔坐标（1/3, 2/3）。因此，这些点是“齐次的（homogeneous，在这里翻译成本质上是相同的）”，因为这些齐次坐标表示都是同一个点（笛卡尔或者欧几里得坐标系）。换句话说，这些齐次坐标是scale invariant（就是说所有分量都乘以一个标量以后表达的值是不变的，标量不变听起来会很奇怪哈）

证明：两个平行线可以相交
笛卡尔空间两个平行直线的方程组：

我们知道在笛卡尔坐标系里面，该方程组无解，因为C ≠ D,如果C=D,两条直线就相同了。

让我们在透视空间里面，用齐次坐标x/w, y/w代替x ,y,

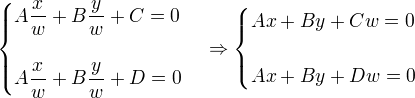
现在我们有一个解(x, y, 0)，两条直线相交于(x, y, 0)，这个点在无穷远处。

5. 更简洁的表达欧氏空间变换

这是齐次坐标最重要的一个优势之一。在以后的学习中你会更加深刻的理解。使用齐次坐标，可以方便的将加法转化为乘法，方便的表达平移。比如我们要完成将2D坐标点x=[u,v]' 平移t=[tu, tv]，如果用非齐次方法的话，是用如下的加法

如果用齐次坐标表示时可以将加法转换为乘法

在欧氏变换中一般有两种操作：旋转和平移。

如果我们想要将向量a进行一个标准的欧氏变换，一般是先用旋转矩阵R进行旋转，然后再用向量t进行平移，其结果a' = R*a + t，这样看起来没什么问题。但是，我们知道SLAM中一般都是连续的欧氏变换，所以会有多次连续的旋转和平移，假设我们将向量a进行了两次欧氏变换，分别为R1, t1 和 R2，t2，分别得到：

b = R1*a + t1, c = R2*b + t2        最终的结果 c = R2*(R1*a + t1) + t2

显然，这样的变换在经过多次后会变的越来越复杂。其根本原因是上述表达方式并不是一个线性的变换关系。此时，齐次坐标就显示出它的魅力了，如果使用齐次坐标来表达 a' = R*a + t 的话可以写为：

旋转和平移可以用一个矩阵T来表示，该矩阵T称为变换矩阵（transform matrix），这样欧氏变换就变成了线性关系，进行多次欧氏变换只需要连乘变换矩阵就行了，比如前面的两次欧氏变换使用齐次坐标就可以表示为：

其中，波浪号代表齐次坐标。一般的，在SLAM中，b = Ta 的形式默认都是齐次坐标。