本节课主要介绍的是数据库系统中的一些Join算法

Nested Loop Join

Naive Nested Loop Join

最简单的Join算法就是遍历两个表中的所有tuple，这会使得内层关系的块被反复读取。假设外层关系R的数据块数量为$M$，tuple数量为$m$，内层关系S的数据块数量为$N$，则总的IO复杂度为$M+m\ast N$。

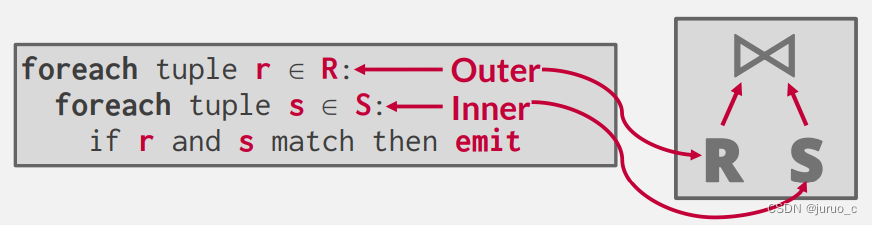
BLock Nested Loop Join

在简单的Naive Nested Loop Join中，没有充分利用内存缓冲页，假设内存缓冲页数量为$B$，则可以一次性加载$B-2$个外层关系R的记录块进行处理，如下图所示。IO复杂度约为$M+\lceil M/(B-2)\rceil \ast N$。

Index Nested Loop Join

在上述两种基本的Nested Loop Join中，性能的瓶颈在于对于外层关系R中的每一个元组，都需要遍历内层关系S中的元组进行判断。可以使用索引对判断进行优化，直接找到内层关系S中符合条件的元组进行输出。具体的做法是，在关系S的连接属性上建立索引，对于R中的每一个元组，根据索引找到对应的S中元组进行连接。假设在索引上查找的代价为$C$，则总IO复杂度为$M+m\ast C$。

Sort-Merge Join

如果两个待连接的关系在连接属性上是有序的，则可以使用合并的方式进行连接。两个关系中的每一个元组均只需遍历一遍，即合并复杂度为$M+N$。如果关系在连接属性上无序，我们可以利用第一节所讲的排序算法进行排序。

Hash Join

Basic Hash Join

基本的Hash Join分为两个阶段：

• Build：遍历外层关系R并在内存中建立哈希表
• Probe：遍历内层关系S，使用已建立的哈希表进行探查

一种常见的优化是使用Bloom Filter。Bloom Filter是一种概率性的数据结构，可以存放于CPU的cache中，用于判断某个Key是否存在于哈希表中。它可能将不存在误判为存在，但是不会将存在误判为不存在。可以在进入哈希表查找之前先查看Bloom Filter。

Partitioned Hash Join

在基本的hash join中，我们需要在内存中对外层关系建立哈希表，当内存不足以存放该哈希表时，可以使用类似聚合的哈希实现方法：

• Build：先使用哈希函数将两个关系的元组分区
• Probe：针对每个分区进行探查处理，可以使用简单的Nested Loop Join

考虑其IO复杂度，Build需要$2\ast (M+N)$，Probe需要$(M+N)$，故总IO复杂度为$3\ast (M+N)$

Conclusion

最后放一张各种算法的对照表