上一篇 文章中, 我们完成了读标注文件和聚类生成 $k$ 个 anchor box, 接下来就是要为特征图的每一个 grid cell $(channels=75)$ 打标签了

上面讲为 每一个 grid cell $(channels=75)$ 打标签 而不为 每一个 anchor box 打标签 , 其实两句话是同一个意思, 但是最终反应到损失函数计算的时候, 其实是计算每个 grid cell 的 $n$ 个通道对应于标签值的损失. 损失函数并不知道什么是 anchor box, 它只管数学上的计算式, 那要计算就需要网络的输出格式与标签格式在数学表达式上的匹配. 将 anchor box 对应的标签信息拉直打平放到 grid cell 的 $n$ 个通道中, 那就是网络输出对应的真值了

在 《保姆级 Keras 实现 YOLO v3 一》 中我们知道网络输出有三个特征图, 三个特征图大小成倍递减, 是为了适应不同尺度的目标. 那一个 ground truth 对应这三个特征图的哪一个呢? 又对应某一特征图中的哪一个 grid cell 呢? 一个 grid cell 中有 $k$ 个 anchor box, 又对应其中的哪一个呢?

一. 分配 anchor box

在 上一篇 文章中, 我们从小到大排列了 $9$ 个聚类出来的 anchor box 尺寸, 有三个特征图, 正好一个特征图可以平均分配三个, 所以前三个就分配给预测小目标的 $52\times 52$ 的特征图, 中间三个就分配给预测中等大小目标的 $26\times 26$ 的特征图, 剩下的三个分配给预测大目标的 $13\times 13$ 的特征图. 这样, 每个特征图的每个 grid cell 就分配到了三个 anchor box

二. 正负样本匹配规则

训练的时候输出是未知的, 我们需要 ground truth 来调整网络的参数, 让输出向 ground truth 靠近. 就需要为每一个输出确定一个靠近的真值用于损失计算

由 YOLO v3 网络结构我们知道在一张图像中有 $13\times 13\times 3+26\times 26\times 3+52\times 52\times 3=10,647$ 个 anchor box, 正负样本的匹配规则如下

• 正样本: 一张图中对于第 $j$ 个 ground truth, 找出包含它的中心点的那个 grid cell 的 $k$ 个 anchor box, 分别计算 $IoU$, 选 $IoU$ 最大的那一个 anchor box 当成正样本. 就算 $IoU$ 低于阈值也当成正样本, 要不然就会出现某个 ground truth 没有对应的 anchor box. 一个 anchor box 只能分配给一个 ground truth
• 负样本: 除正样本外, 对第 $i$ 个 anchor box, 遍历一张图中所有 ground truth, 记录最大的 $IoU$ 值, 如果最大的 $IoU$ 小于阈值, 那这个 anchor box 就是负样本
• 忽略样本: 除正负样本外, 都为忽略样本

按照上面的规则会有一个小问题, 就是正样本会很少, 因为 ground truth 的数量等于正样本的数量, 而一张图中的目标通常是很少的, 所以就会造成样本不均衡. 要解决这个问题就需要修改一下正样本的匹配规则, 修改后如下

• 正样本: 一张图中对于第 $j$ 个 ground truth, 找出包含它的中心点的那个 grid cell 的 $k$ 个 anchor box, 分别计算 $IoU$, 选 $IoU$ 最大的那一个 anchor box 当成正样本. 就算 $IoU$ 低于阈值也当成正样本. 对于剩下的 $k-1$ 个 anchor box, 如果它与第 $j$ 个 ground truth 的 $IoU$ 大于一个较大的阈值, 比如 $0.7$, 都将这些 anchor box 分配为 第 $j$ 个 ground truth 的正样本. 一个 anchor box 只能分配给一个 ground truth

在有一些实现中, 计算正样本的 $IoU$ 时, 将 ground truth 和 anchor box 的一个角移动到相同的位置, 比如下图, 将左上角移动到相同的位置. 计算方式就和聚类时计算 $IoU$ 是一样的

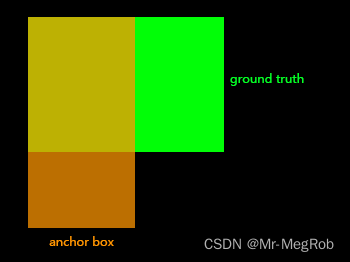
两个方式其实差异不大, 因为 ground truth 和 anchor box 的中心距离并不远, 所以交集面积是差不多的, 甚至大部分计算结果是一样的. 这也就导致了两种计算方式差异不大

三. 为每一个 anchor box 打标签

3.1 anchor box 长什么样?

网络输入是 $416\times 416$, $52\times 52$ 的特征图相比于原图缩小了 $8$ 倍, 所以在原图中每隔 $8$ 个像素放三个最小尺寸的 anchor box, 三个 anchor box 中心重叠. 如下图, 图中一个小格表示一个像素

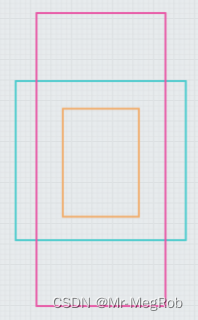
$26\times 26$ 的特征图缩小了 $16$ 倍, 所以就是每隔 $16$ 个像素放三个中等尺寸的 anchor box, 类推 $13\times 13$ 特征图每隔 $32$ 个像素就放最大的三个 anchor box

3.2 每一个 anchor box 标签需要填充的信息有哪些?

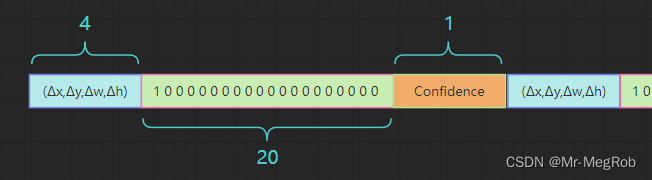
我们要预测 anchor box 的修正量 $(\Delta x,\Delta y,\Delta w,\Delta h)$, 类别($20$ 类), 还有要有一个置信度 $C\in [0,1]$, 所以一个 anchor box 需要的参数有 $25$ 个, 一个 grid cell 有 $3$ 个 anchor box, 所以一个 grid cell 需要 $75$ 个参数, 这 $75$ 个参数就填充一个 grid cell 的 $75$ 个通道, $3$ 个 anchor box 的数据依次排列即可, 你要喜欢也可以按你想的顺序排列

3.3 $(\Delta x,\Delta y,\Delta w,\Delta h)$ 怎么填?

我们要清楚一点, 网络对目标位置预测的是对于 anchor box 变换到 ground truth 的修正量 $(\Delta x,\Delta y,\Delta w,\Delta h)$, 而不是直接预测目标的绝对坐标位置, 现在看图说话

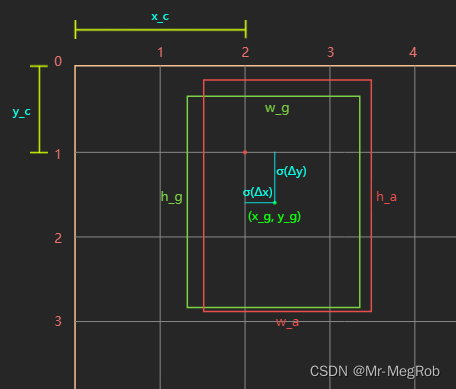
上图中, 绿色框表示 ground truth, 坐标表示形式是 $(x,y,w,h)$, 其中 $x,y$ 表示中心坐标, $w,h$ 表示宽和高, 对应到图中便是 $(x_g,y_g,w_g,h_g)$, 红色框表示一个 anchor box. 它的中心是 grid cell 的坐标 $(x_c,y_c)$, 其宽和高分别是 $w_a,h_a$. 好了, 现在我们用网络的输出 $(t_x,t_y,t_w,t_h)$ 来修正 anchor box, 之所以用 $(t_x,t_y,t_w,t_h)$ 来表示预测值, 是因为我们要用 $(\Delta x,\Delta y,\Delta w,\Delta h)$ 来表示标签值. 不要弄混了. 公式如下
$$\begin{array}{rl}{x}_g& =\sigma (t_x)+x_c\\ y_g& =\sigma (t_y)+y_c\\ w_g& =w_a{e}^{t_w}\\ h_g& =h_a{e}^{t_h}\end{array}$$
其中 $\sigma (x)=1/(1+e^{-x})$, 函数图像如下

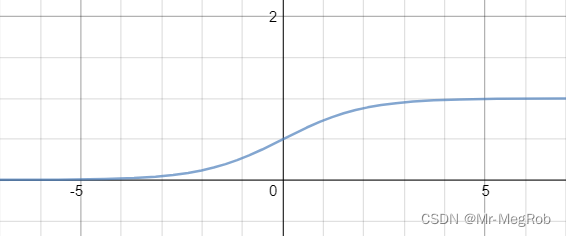
所以 $\sigma (t_x)\in (0,1)$, $\sigma (t_y)\in (0,1)$. 这样就将中心点限制在了 grid cell 内部. 而用 $e$ 指数则可以保证 $w_a{e}^{t_w}$ 和 $h_a{e}^{t_h}$ 大于 0, 因为 $w_g$ 和 $h_g$ 必须大于 0

所以, 我们希望网络的输出 $(t_x,t_y,t_w,t_h)$ 代入上面的公式之后, 能得到或者接近$(x_g,y_g,w_g,h_g)$ , 但是 $(t_x,t_y,t_w,t_h)$ 的值要是多少才合适呢?

$(x_g,y_g,w_g,h_g)$, $(x_c,y_c,w_a,h_a$) 是已知量, 解上面的等式就可以得到 $(t_x,t_y,t_w,t_h)$,
$$\begin{array}{rl}{t}_x& =ln(\frac{x_g-x_c}{1-x_g+c_x})\\ t_y& =ln(\frac{y_g-y_c}{1-y_g+c_y})\\ t_w& =ln(\frac{w_g}{w_a})\\ t_h& =ln(\frac{h_g}{h_a})\end{array}$$
现在, 解出来的 $(t_x,t_y,t_w,t_h)$ 就是标签值 $(\Delta x,\Delta y,\Delta w,\Delta h)$

$x_c,y_c$ 有必要要另外说明一下, 两个都是整数, 因为它们是 grid cell 的坐标, 范围是 $[0,$ 特征图尺寸 $-1]$, 如果哪一个 grid cell 中的 anchor box 负责预测目标, 那么这个 anchor box 的一部分坐标就已知了, 剩下的就是预测这个 anchor box 的中心坐标相对于这个 grid cell 左上角坐标 $(x_c,y_c)$ 的偏移量.

还是以上面的图用具体的数字来说明, 假设上面的图是 $52\times 52$ 的特征图对应的原图, 那一个格子宽度是 8 个像素, 一个格子对应特征图一个 grid cell, 此时 ground truth 绝对坐标是 $(18.82,12.98,17,20)$, anchor box 的尺寸是 $(16,22)$. 从图中可以看到 $c_x=2,c_y=1$, 则 $\sigma (\Delta x)=0.3525,\sigma (\Delta y)=0.6225$, $0.3525$ 和 $0.6225$ 这两个数字怎么来的?

因为 ground truth 中心点绝对坐标是 $(18.82,12.98)$, 相对于 grid cell 左上角的坐标是
$$(18.82-8x_c,12.98-8y_c)=(2.82,4.98)$$
再将 $(2.82,4.98)$ 以步长 $8$ 为分母归一化得到 $(0.3525,0.6225)$, 所以 ground truth 归一化后的中心坐标为 $(2.3525,1.6225)$, 公式中的 $(x_g,y_g)$ 就是归一化后的坐标. 如果要还原成绝对坐标, 将 $(2.3525,1.6225)$ 乘以 $8$ 就可以得到 $(18.82,12.98)$

反解 $\sigma (\Delta x)=0.3525,\sigma (\Delta y)=0.6225$, 再将 $w_g,h_g,w_a,h_a$ 再入
$$\begin{array}{rl}\Delta w& =ln(\frac{w_g}{w_a})\\ \Delta h& =ln(\frac{h_g}{h_a})\end{array}$$
将就可以解出 $(\Delta x,\Delta y,\Delta w,\Delta h)=(-0.608068,0.500173,0.060625,-0.095310)$, 所以这个 anchor box 的关于位置的标签值就是 $(-0.608068,0.500173,0.060625,-0.095310)$

其实将 $\sigma (\Delta x)$ 与 $\sigma (\Delta y)$ 限制在 $(0,1)$ 是有一点问题的, 因为 $\Delta x$ 和 $\Delta y$ 趋于 $-\infty$ 时 $\sigma (x)$ 才能取到 $0$, 趋于 $+\infty$ 时 $\sigma (x)$ 才能取到 $1$. 所以当 ground truth 中心点在 grid cell 边界的时候是学习不到这个值的. 不过这个也不是什么大问题, 当 $|t_x|$ 和 $|t_y|$ 大于 $5$ 后, 就已经很接近了. 但是打标签会有问题, 因为按上面的公式计算出来的值是 $-\infty$ 或者 $+\infty$. 为了解决一个问题, 可以有两种方法, 一是打标签的时候, 把标签值的绝对值限制在某个范围内, 比如 $5$, $\sigma (5)=0.9933071491$, 算是一个比较接近的数了. 另一个更好的方法是在 将 $\sigma (x)$ 修改成
$$k\sigma (x)-b$$
其中 $k>1,b>0$. 假设 $k=2,b=0.5$, 这样的话, 假设 $2\sigma (\Delta x)-0.5=0.99$, 则标签值 $\Delta x=1.072120$, 假设 $2\sigma (\Delta x)-0.5=0.01$, 则标签值 $\Delta x=-1.072120$, 这很合理. 这就是在 YOLO v4 中的改进方法, 本文就选这种方法修正这个问题

3.4 类别标签怎么填?

这个很简单, $20$ 个类别, 只要按 one-hot 编码填进去就可以了, 在 $3.2$ 节的图中就是一个例子

3.5 置信度标签怎么填?

这个更简单, 如果是负样本填 $0$, 正样本就填 $1$, 忽略的样本呢? 这个看你的心情了, 只要不是 $0$ 或者 $1$ 就行, 为了更好的区分, 我就填 $-1$

四. 打标签代码

既然要为 anchor box 打标签, 那首先要生成 anchor box

# 生成 anchor box 函数
# image_size: 图像尺寸
# anchor_size: 聚类生成的 anchor box 尺寸
def create_anchors(image_size, anchor_size):# 生成基础的 k 个 anchor boxbase_anchors = []for s in anchor_size:base_anchors.append((-s[0] // 2, -s[1] // 2, s[0] // 2, s[1] // 2))grid_anchors = len(anchor_size) // 3 # 每个特征图中一个 grid cell 包含的 anchor box 的数量anchor_boxes = [] # 存放各特征图生成的 anchor box 的列表# 生成三种尺寸特征图的 anchor boxfor i, stride in enumerate(STRIDES):# 特征图尺寸feature_rows = image_size[0] // stridefeature_cols = image_size[1] // stride# 中心坐标ax = (tf.cast(tf.range(feature_cols), tf.float32)) * stride + stride // 2ay = (tf.cast(tf.range(feature_rows), tf.float32)) * stride + stride // 2ax, ay = tf.meshgrid(ax, ay)# 变换形状方便下面的 tf.stackax = tf.reshape(ax, (-1, 1))ay = tf.reshape(ay, (-1, 1))# stack([ax, ay, ax, ay]) 成这样的格式, 是为了分别加上 base_anchor 的左上角坐标和右下角坐标boxes = tf.stack([ax, ay, ax, ay], axis = -1)# boxes: (x1, y1, x2, y2) = 中心坐标 + base_anchors, 一种尺寸的特征图取 3 个 anchor box        boxes = boxes + base_anchors[i * grid_anchors: i * grid_anchors + grid_anchors]anchor_boxes.append(boxes)# 将三个特征图的 anchor box 放到一个 Tensor 中, 最后 shape == (n, 4)feature_boxes = tf.concat([anchor_boxes[0], anchor_boxes[1], anchor_boxes[2]], axis = 0)feature_boxes = tf.reshape(feature_boxes, (-1, 4))return feature_boxes

测试 create_anchors 函数

# 测试 create_anchors 函数
anchor_boxes = create_anchors((LONG_SIDE, LONG_SIDE), cluster_anchors)
print(anchor_boxes)

打印结果

tf.Tensor(
[[ -4.  -7.  12.  15.][ -9. -25.  17.  33.][-20. -13.  28.  21.]...[277. 333. 522. 467.][322. 286. 478. 514.][245. 268. 555. 531.]], shape=(10647, 4), dtype=float32)

因为打标签时会用到 $IoU$, 所以先定义一个函数计算 $IoU$

# 计算 IoU 函数
# gt_box: 一个标注框
# anchor_boxes: n 个 anchor box, shape = (n, 4)
def get_iou(gt_box, anchor_boxes):x = tf.maximum(gt_box[0], anchor_boxes[:, 0])y = tf.maximum(gt_box[1], anchor_boxes[:, 1])w = tf.maximum(tf.minimum(gt_box[2], anchor_boxes[:, 2]) - x, 0)h = tf.maximum(tf.minimum(gt_box[3], anchor_boxes[:, 3]) - y, 0)intersection = w * hgt_area = (gt_box[2] - gt_box[0]) * (gt_box[3] - gt_box[1])box_area = (anchor_boxes[:, 2] - anchor_boxes[:, 0]) * (anchor_boxes[:, 3] - anchor_boxes[:, 1])union = gt_area + box_area - intersectionious = intersection / unionreturn tf.reshape(ious, (-1, 1))

测试 $IoU$

# 测试 IoU
a = (8, 8, 32, 64)
b = [(3, 3, 32, 65), (6, 3, 35, 70), (20, 15, 40, 70), (80, 100, 128, 160)]
print("iou(a, b) =", get_iou(a, np.array(b)))

测试结果

iou(a, b) = tf.Tensor(
[[0.74749722][0.69171384][0.31681034][0.        ]], shape=(4, 1), dtype=float64)

在打位置标签 $(\Delta x,\Delta y,\Delta w,\Delta h)$ 的时候, 需要作一些计算, 我们把这些计算也放到一个函数中去方便使用

# 位置标签函数
# gt_box: 一个标注框
# anchor_boxes: 一张图中所有 anchor box
def get_delta(gt_box, anchor_boxes):# 返回值, 返回一个 gt_box 与所有 anchor box 之间的修正量# 计算时把所有的 anchor box 当成正样本, 后面会根据 IoU 筛选出真正的正样本deltas = None# gt_box 在原图中的 (x, y, w, h) 形式坐标gt_x = (gt_box[0] + gt_box[2]) * 0.5gt_y = (gt_box[1] + gt_box[3]) * 0.5gt_w = (gt_box[2] - gt_box[0])gt_h = (gt_box[3] - gt_box[1])# anchor box 在原图中的宽和高a_w = anchor_boxes[..., 2] - anchor_boxes[..., 0]a_h = anchor_boxes[..., 3] - anchor_boxes[..., 1]# 每种特征图的 anchor box 数量 (52 × 52 × 3, 26 × 26 × 3, 13 × 13 × 3)anchor_num = [(LONG_SIDE // s) * (LONG_SIDE // s) * 3 for s in STRIDES]# 不同特征图 anchor box 切片索引idx_start = 0idx_end = anchor_num[0]for i in (0, 1, 2):# gt_box 中心点在特征图中距 grid cell 左上角的距离dist_x = tf.constant(gt_x / STRIDES[i] - round(gt_x) // STRIDES[i],shape = (anchor_num[i],), dtype = tf.float32)dist_y = tf.constant(gt_y / STRIDES[i] - round(gt_y) // STRIDES[i],shape = (anchor_num[i],), dtype = tf.float32)# 坐标计算公式为 2 * sigma(x) - 0.5delta_x = tf.math.log((0.5 + dist_x) / (1.5 - dist_x))delta_y = tf.math.log((0.5 + dist_y) / (1.5 - dist_y))# 每个尺寸的特征图的 anchor box 数量不一样, 所以要加以区分delta_w = tf.math.log(gt_w / a_w[idx_start: idx_end])delta_h = tf.math.log(gt_h / a_h[idx_start: idx_end])idx_start = idx_endidx_end = idx_end + (anchor_num[i + 1] if i < 2 else sum(anchor_num))if None == deltas:deltas = tf.stack([delta_x, delta_y, delta_w, delta_h], axis = -1)else:deltas = tf.concat([deltas, tf.stack([delta_x, delta_y, delta_w, delta_h], axis = -1)], axis = 0)return deltas

为了方便计算, get_delta 在函数内部我们假设所有的 anchor box 都是正样本, 这样计算也不影响, 因为损失函数中我们只关心真正的正样本, 至于其他样本是什么值并不影响

因为只有 ground truth 中心所在的 grid cell 中的 $k$ 个 anchor box 才负责预测, 所以我们要把这 $k$ 个 anchor box 的序号找出来, 方便后面函数的操作

# 计算 ground truth 所在 grid cell 的 k 个 anchor box 的序号
# 一共有 10647 个, 返回的是在三个特征图中的位置序号
def get_valid_idx(gt_box):# 每种特征图的 anchor box 数量 (52 × 52 × 3, 26 × 26 × 3, 13 × 13 × 3)anchor_num = [(LONG_SIDE // s) * (LONG_SIDE // s) * 3 for s in STRIDES]# 一个 grid cell 中的 anchor box 数量grid_anchors = (CLUSTER_K // 3)# gt_box 在原图的中心坐标x = (gt_box[0] + gt_box[2]) * 0.5y = (gt_box[1] + gt_box[3]) * 0.5# 后面的特征图中 anchor box 的序号要加上前面的特征图的总的 anchor box 的数量offset = [0, anchor_num[0], anchor_num[0] + anchor_num[1]]# 返回值ret_idx = []for i in (0, 1, 2):grid_x = round(x) // STRIDES[i]grid_y = round(y) // STRIDES[i]# 在各特征图中的起始序号idx_start = grid_y * (LONG_SIDE //  STRIDES[i]) * grid_anchors + grid_x * grid_anchors + offset[i]ret_idx.append(idx_start)# 后面 grid_anchors - 1 个 anchor box 序号顺序增加for j in range(1, grid_anchors):ret_idx.append(ret_idx[-1] + 1)return ret_idx

# 测试 get_valid_idx 函数
valid_boxes = get_valid_idx((0, 0, 8, 8))
print(valid_boxes)

输出结果

[0, 1, 2, 8112, 8113, 8114, 10140, 10141, 10142]

现在定义一个函数, 为一张图像的 anchor box 打标签

# 定义打标签函数
# gts: get_ground_truth 函数的第三个返回值, 前两个在这里用不上, 所以下面的循环中只用了最后一个
# anchor_boxes: create_anchors 函数生成的 anchor box
def get_label(gts, anchor_boxes):# 总的 anchor box 数量anchor_nums = anchor_boxes.shape[0]# 类别数量categories = len(CATEGORIES)# 位置标签(Δx,Δy,Δw,Δh), 全部初始化为 0deltas = tf.zeros((anchor_nums, 4), dtype = tf.float32)# 各 gt_box 与 anchor box 的最大 IoU, 要比较各 gt_box 与所有 anchor box IoU 的大小# 把最大值记录下来, 这样将标签分配给最合适的 anchor box, 还有一个功能是用来判断是否是负样本max_ious = tf.zeros((anchor_nums, 1), dtype = tf.float32)# 类别标签, 全部初始化为 0cls_ids = tf.zeros((anchor_nums, categories), dtype = tf.float32)# 置信度标签, 全部初始化为 -1, 表示忽略样本confidence = tf.fill((anchor_nums, 1), -1.0)for gt_box, cls_id in gts[-1]:# 所有 anchor box 的可用状态, 只有 gt_box 所在 grid cell 的 k 个 anchor box 可用, 先全部初始化为 Falsevalid_mask = tf.fill((anchor_nums, 1), False)# 取出 gt_box 所在 grid cell 的 k 个 anchor box 的序号indices = get_valid_idx(gt_box)indices = tf.reshape(tf.constant(indices), (-1, 1))updates = tf.constant(True, shape = indices.shape)# 将序号位置的 False 变成 Truevalid_mask = tf.tensor_scatter_nd_update(valid_mask, indices, updates)# 正常计算 IoU# ious = get_iou(gt_box, anchor_boxes)# 聚类方式计算 IoU, gt_box 与 所有 anchor box 的 IoU, 左上角都在 (0, 0)ious = cluster_iou((gt_box[2] - gt_box[0], gt_box[3] - gt_box[1]),tf.stack([anchor_boxes[:, 2] - anchor_boxes[:, 0],anchor_boxes[:, 3] - anchor_boxes[:, 1]], axis = -1))# 聚类方式计算 IoU 结果要变换到合适的 shapeious = tf.reshape(ious, (anchor_nums, -1))# 屏蔽掉其他 grid cell 的 IoUious = tf.where(valid_mask, ious, 0.0)# 找出最大值所在的位置grater_mask = ious > max_ious# 记录每次比较的最大值, 这个是在不同的 gt_box 这间比较max_ious = tf.maximum(ious, max_ious)# 获取当前 gt_box 与 anchor box IoU 最大值和对应的索引,# k = 1, 表示我们只关心最大的一个, 这个也许是小于阈值的, 但是我们也要将其变成正样本_, indices = tf.math.top_k(tf.reshape(ious, (anchor_nums, )), k = 1)     # 创建掩码, 只有最大值位置为 True, 其他为 Falsemax_mask = tf.cast(tf.one_hot(indices, depth = anchor_nums), dtype = tf.bool)max_mask = tf.reshape(max_mask, (-1, 1))# 将 IoU >= POS_THRES 的也标记成 True, 这样可以增加正样本数量, 再将 max_mask 加入到 pos_maskpos_mask = ious >= POS_THRESpos_mask = tf.logical_or(max_mask, pos_mask)# 与 grater_mask 做 and 是因为当前 gt_box 匹配的 IoU 要大于之前匹配的# 才能变更这个 anchor box 的标签, 要不然就是之前的标签更合适pos_mask = tf.logical_and(pos_mask, grater_mask)# 将 deltas 正样本位置替换成计算好的标签值deltas = tf.where(pos_mask, get_delta(gt_box, anchor_boxes), deltas)# 当前 gt_box 的整数类别转换成 one-hotone_hot = tf.reshape(tf.one_hot(cls_id, depth = categories), (-1, 20))# 将 cls_ids 对应位置替换成当前 gt_box 的 one-hot 标签cls_ids = tf.where(pos_mask, one_hot, cls_ids)# 将正样本位置置信度替换成 1confidence = tf.where(pos_mask, 1.0, confidence)# 循环完成后, confidence 中只有正样本和忽略样本, 还没有负样本# 找出 confidence 所有正样本的位置pos_mask = confidence > 0# 由 max_ious 定位出所有小于阈值的位置neg_mask = max_ious < NEG_THRES# 从 neg_mask 中去除 pos_mask 位置neg_mask = tf.where(pos_mask, False, neg_mask)# 将负样本位置的值替换成 0confidence = tf.where(neg_mask, 0.0, confidence)# 组合成总的标签信息# 现在 label 的格式为 (位置标签, 类别标签, 置信度), shape = (10647 × 25)# 如果 reshape 可变成 75 个通道, 只是这样就要分成三个 tensor 了, 没有必要label = tf.concat([deltas, cls_ids, confidence], axis = -1)# 最后返回 max_ious 是不需要的, 只是为了查看每个 ancor box 与 ground truth 的 IoUreturn label

测试函数

# 测试打标签函数
gts = get_ground_truth(label_data[1], label_data[2], CATEGORIES)
label = get_label(gts, anchor_boxes)
# 找出最后一维值为 1 的行, 也就是正样本
pos_mask = tf.equal(label[:, -1], 1)
pos_targets = tf.boolean_mask(label, pos_mask)
print(pos_targets)

输出结果

tf.Tensor(
[[-0.6466271   0.          0.09909087  0.38566247  1.          0.0.          0.          0.          0.          0.          0.0.          0.          0.          0.          0.          0.0.          0.          0.          0.          0.          0.1.        ][-1.0986123   0.2513144   0.08004274  0.38566247  1.          0.0.          0.          0.          0.          0.          0.0.          0.          0.          0.          0.          0.0.          0.          0.          0.          0.          0.1.        ][-0.3794896   0.7884574   0.01869218 -0.44055638  1.          0.0.          0.          0.          0.          0.          0.0.          0.          0.          0.          0.          0.0.          0.          0.          0.          0.          0.1.        ][-0.6466271   0.12516314  0.01869218 -0.44055638  1.          0.0.          0.          0.          0.          0.          0.0.          0.          0.          0.          0.          0.0.          0.          0.          0.          0.          0.1.        ][-0.8622235  -0.18805222  0.         -0.42285687  1.          0.0.          0.          0.          0.          0.          0.0.          0.          0.          0.          0.          0.0.          0.          0.          0.          0.          0.1.        ][ 0.06252041 -0.2513144   0.03704124 -0.5146644   1.          0.0.          0.          0.          0.          0.          0.0.          0.          0.          0.          0.          0.0.          0.          0.          0.          0.          0.1.        ]], shape=(6, 25), dtype=float32)

找到 $6$ 个正样本, 将它们画到原图上

# 将找出来的正样本 anchor box 显示到原图, gt_box 已经在前面画过了
indices = tf.where(tf.equal(label[:, -1], 1.0))
for t in indices:t = t.numpy()[0]box = anchor_boxes[t].numpy()print(box)cv.rectangle(img_copy, (round(box[0]), round(box[1])), (round(box[2]), round(box[3])),(0, 0, random.randint(128, 256)), 2)plt.figure("label_box", figsize = (8, 4))
plt.imshow(img_copy[..., : : -1])
plt.show()

[ 44. 203.  92. 237.]
[ 60. 275. 108. 309.]
[333.  60. 386. 147.]
[141.  76. 194. 163.]
[ 29.  92.  82. 179.]
[157. 172. 210. 259.]

五. 代码下载

示例代码可下载 [Jupyter Notebook 示例代码] (还未上传)

上一篇: 保姆级 Keras 实现 YOLO v3 二
下一篇: 保姆级 Keras 实现 YOLO v3 四 (待续…)