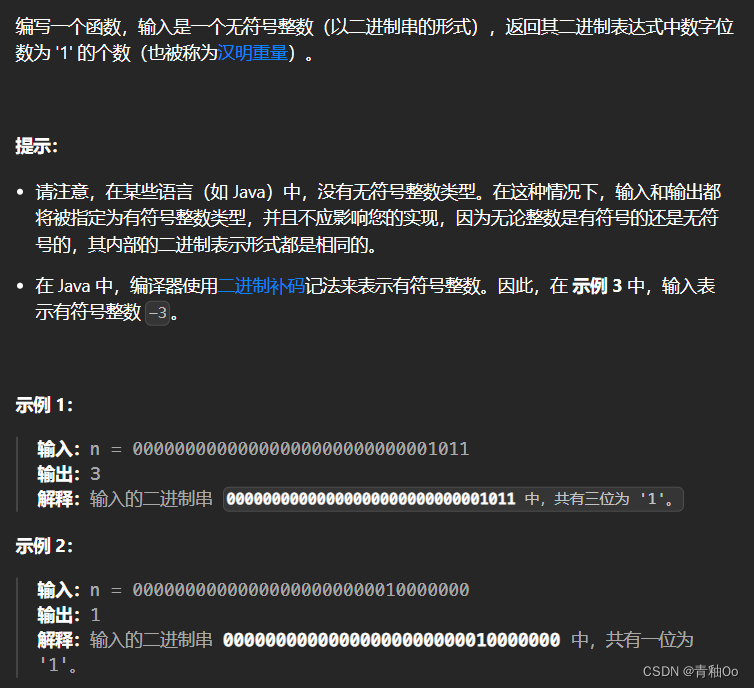
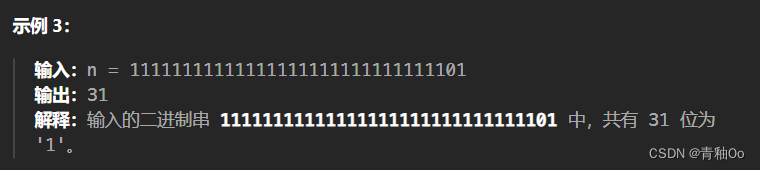
位1的个数
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.mzph.cn/news/219251.shtml
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
项目经理和产品经理该如何选择?
最近很多人咨询“项目经理跟产品经理该怎么选,我更适合哪个?”“项目经理跟产品经理哪个更有钱途 ”“项目经理转产品经理好转吗”等等,今天就一次性说清楚项目经理跟产品经理有什么区别,应该怎么选择。
不想看长篇大论的&#x…
Python+Pytest接口自动化之HTTP协议基础
HTTP协议简介
HTTP 即 HyperText Transfer Protocol(超文本传输协议),是互联网上应用最为广泛的一种网络协议。所有的 WWW 文件都必须遵守这个标准。
设计 HTTP 最初的目的是为了提供一种发布和接收 HTML 页面的方法。HTTP 协议在 OSI 模型…
Kubernetes版本升级到v1.18.0方法
升级k8s版本才能使用kube-prometheus安装监控
1、查看集群状态
[rootk8s-master k8s-script]# kubectl get nodes
NAME STATUS ROLES AGE VERSION
k8s-master Ready master 5d22h v1.18.0
k8s-slave1 Ready <none> 4d10h v1.18.0
k…
ActiveMQ使用指南
介绍
ActiveMQ是Apache开源组织旗下的一个项目,是一个流行的开源消息中间件。它完全支持JMS1.1和J2EE1.4规范的JMS Provider实现,并且是纯Java开发的产品。ActiveMQ支持多种语言编写客户端,包括C,C,C#,Perl,PHP,Ruby,Ajax等,同时…
php5, php7,php8 有什么区别
PHP 5、PHP 7 和 PHP 8 是 PHP 编程语言的不同版本,它们之间有许多改进和变化。以下是它们的一些主要区别:
1. 性能提升: PHP 5: PHP 5.x 版本的性能相对较低,特别是在处理大量并发请求和执行大型应用程序时。 PHP 7…
做数据分析为何要学统计学(6)——什么问题适合使用卡方检验?
卡方检验作为一种非常著名的非参数检验方法(不受总体分布因素的限制),在工程试验、临床试验、社会调查等领域被广泛应用。但是也正是因为使用的便捷性,造成时常被误用。本文参阅相关的文献,对卡方检验的适用性进行粗浅…
【unity】如何用Unity获取Windows桌面
【背景】
默认的Unity可实现的屏幕共享仅仅针对Unity编辑器的编辑窗口中的Camera展现的内容。本篇研究如何实现用Unity实时反映Windows桌面窗口画面。
【准备插件】
下载地址: https://download.csdn.net/download/weixin_41697242/88623496
将解压后的文件夹直…
Feign-自定义配置
目录
一、自定义Feign配置
二、修改日志级别
方式一:application配置文件方式
方式二:java代码方式 三、总结 一、自定义Feign配置 二、修改日志级别 配置Feign日志有两种方式
方式一:application配置文件方式 (1)…
目标检测DOTA数据集提取感兴趣类别数据
DOTA数据集
DOTA数据集包含2806张航空图像,尺寸大约从800x800到4000x4000不等,包含15个类别共计188282个实例。其标注方式为四点确定的任意形状和方向的四边形(区别于传统的对边平行bbox)。类别分别为:plane, ship, s…
交易历史记录20231205 记录
昨日回顾: select top 10000 * from dbo.CODEINFO A left join dbo.全部A股20231205010101 B ON A.CODE B.代码 left join dbo.全部A股20231205CONF D on A.CODED.代码left join dbo.全部A股20231205 G on A.CODEG.代码 left…
LeetCode-合并有序链表问题
1.合并两个有序链表
题目描述:
将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。 思路: 首先建立一个头节点方便后续操作,然后开始循环将两个链表的节点值进行比较,如果list1…
A Piece of Cake
A Piece of Cake
题目链接
题意 输出一个整数表示a[n]的总和 思路 输入数组a[n]在for循环中确定数学式子ans等于它本身加上数学式子 坑点 for循环中i要从0开始,不然a[1] 2 x a[2] 3 x a[3] … a[0] x a[a[0]]的值就会出错,2 x a[2]就会变成 3 x a[…
fastapi实现websocket在线聊天
最近要实现一个在线聊天功能,基于fastapi的websocket实现了这个功能。下面介绍一下遇到的技术问题
1.问题难点
在线上环境部署时,一般是多进程的方式进行部署启动fastapi服务,而每个启动的进程都有自己的独立存储空间。导致存储的连接对象分…
Windows Subsystem for Linux (WSL) 安装与使用笔记
文章目录 Part.I IntroductionPart.II 安装Chap.I 安装流程Chap.II 迁移至其他盘 Part.III 使用Chap.I 一些信息Chap.II 配置下载软件的源Chap.III 安装 pip Reference Part.I Introduction
Windows Subsystem for Linux 简写为 WSL,是 Windows 的一个 Linux 子系统…
常用的建表但范式、反规范化
规范化: 规范化是用于数据库设计的一系列原理和技术,它可以减少表中数据的冗余,增加数据完整性和一致性。通常有很多范式。 第一范式(1NF):
常用的三种范式:
表中的字段都是不可再分割的原子属…
vue/uniapp - 返回上一页并onLoad/onShow刷新数据列表接口
目录 详情页(detail.vue):列表页(list.vue)大佬最后 在uni中,返回页面是不会触发
onLoad方法的; 如果我们只想在特定情况下返回上一页才需要刷新数据,那么用onShow的话,那刷新就太频繁了;
这时候…
蝴蝶Butterfly 数据集VOC+yolo-2000张(labelImg标注)
蝴蝶被誉为“会飞的花朵”,是一类非常美丽的昆虫。蝴蝶大多数体型属于中型至大型,翅展在15~260毫米之间,有2对膜质的翅。体躯长圆柱形,分为头、胸、腹三部分。体及翅膜上覆有鳞片及毛,形成各种色彩斑纹。今天要介绍的是…
C++类模板案例-实现一个通用的数组类
案例中用到的方法
可以对内置数据类型以及自定义数据类型的数据进行存储将数组中的数据类型存储到堆区构造函数中可以传入数组的容量提供对应的拷贝构造函数以及operator防止浅拷贝问题提供尾插法和尾删法对数组中的数据进行增加和删除可以通过下标的方式访问数组中的元素可以…





——什么问题适合使用卡方检验?)








 安装与使用笔记)


)

)