详情请参考:https://dev.mysql.com/doc/refman/8.0/en/innodb-storage-engine.html
- InnoDB 是一个通用目的的存储引擎,它在高可用性、高性能方面做了平衡。
- MySQL 8.0,InnoDB 是默认的存储引擎。在创建表的时候,如果没有使用ENGINE
子句指明不同的存储引擎,那么mysql会创建一个InnoDB的表。 - 在进行DML操作的时候(例如insert,update,delete),InnoDB
支持事务特性,例如提交、回滚、崩溃恢复能力。 - 行级别的锁定和一致性读,提升了多个用户的并发性和性能。
- InnoDB 在磁盘上存储表,基于主键来优化查询。每一个InnoDB 表有一个主键索引,称为簇(集群)索引,这样组织数据,以便用主键查询的时候最小化I/O。
- InnoDB 支持外键( FOREIGN KEY)约束,来保持数据的完整性。利用外键约束,在 insert、update、和delete 操作的时候会进行检查,以确保不会导致相关的表不一致。
下面这个表来自mysql官网:

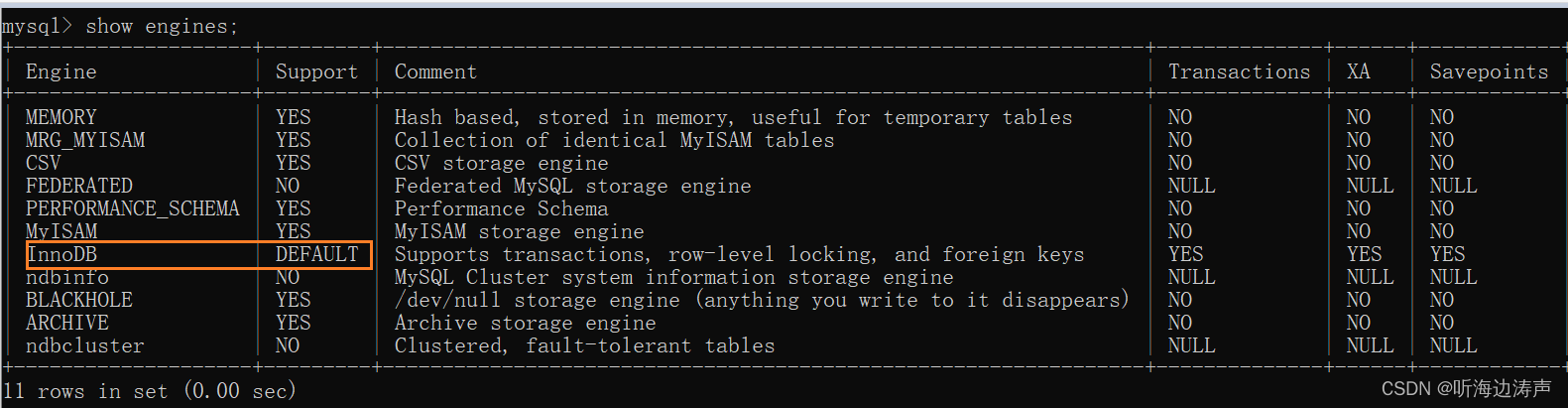
在mysql的cmd窗口,可以使用命令show engines;来查看InnoDB 是不是默认的存储引擎:











】)
Tiki-taka算法(TTA)求解无人机三维路径规划研究(MATLAB))
 WITHIN GROUP () 行转列函数使用)





