问题

今天做2020年的数一真题时发现，这个知识点似乎是在教辅书中没太提到过，有些困惑，特此总结。

思考

设级数收敛半径为R。

1. 正项级数：当|x|<R时，级数收敛，子级数必然收敛（设原级数和函数收敛于S0，则子级数必小于S0，即子级数的数列有上界，且单调递增，因此收敛）当 |x|=R时，单独判断，而级数的收敛性是要小于子级数的。当|x|>R时，级数发散，子级数可能收敛可能发散。
2. 任意项级数：当|x|<R时，级数收敛，子级数必然收敛（因为原级数绝对收敛，子级数必有上界），当 |x|=R时，单独判断，而级数的收敛性和子级数的收敛性关系不确定（因为原级数可能项与项之间相互抵消，导致收敛性小于子级数）。当|x|>R时，级数发散，子级数可能收敛可能发散。

总结

总的来说，对于任意项级数，除了在收敛半径内子级数绝对收敛外，别的地方和原级数无关，对于正项级数，和任意项级数不同的点就在于，在边界上时，收敛性是要高于原级数的。

tip：突然感觉，这个和函数就像是二维数列。如下图：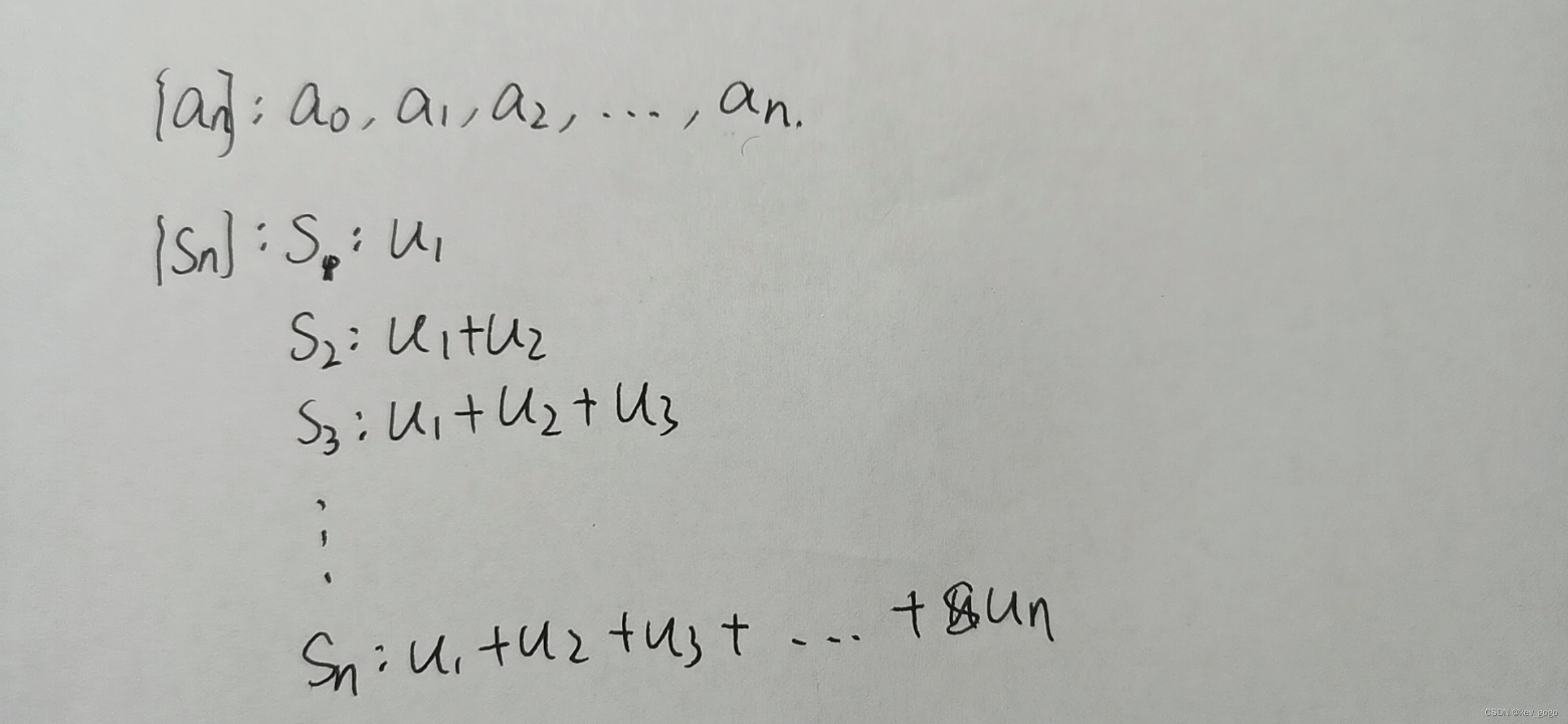
其中，数列收敛和和Sn收敛的含义是一样的，都是单调递增有上界或单调递减有下界收敛。
Sn特殊的地方在于，他的通项每一项都是一个数列的元素的和函数。
但是本质上来说，和函数依旧是一个数列，其通项为Sn。