文档讲解：代码随想录

视频讲解：代码随想录B站账号

状态：看了视频题解和文章解析后做出来了

 309.最佳买卖股票时机含冷冻期

class Solution:def maxProfit(self, prices: List[int]) -> int:n = len(prices)if n < 2:return 0dp = [[0]*3 for _ in range(len(prices))]dp[0][0] = -prices[0]for i in range(1, len(prices)):dp[i][0] = max(dp[i-1][0], dp[i-1][2] - prices[i])dp[i][1] = dp[i-1][0] + prices[i]dp[i][2] = max(dp[i-1][2], dp[i-1][1])return max(dp[-1][1], dp[-1][2])

• 时间复杂度：O(n)
• 空间复杂度：O(n)

1. 确定dp数组以及下标的含义

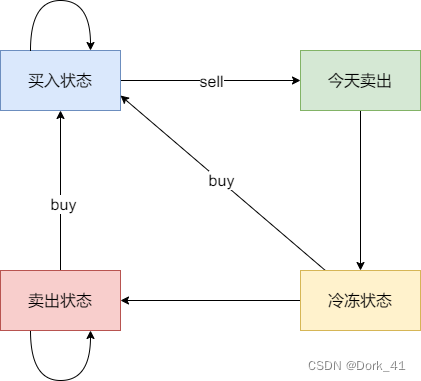
这道题引入了冷冻期的概念，也就是卖出以后有一天不能交易。

这里需要定义三个状态：

（1）状态0：持有股票

（2）状态1：不持有股票且进入冷冻期

（3）状态2：不持有股票且不在冷冻期

2. 确定递推公式

- 状态0的持有股票有两种情况，第一种是延续昨天持有的状态，第二种是今天买了股票：

dp[i][0] = max(dp[i-1][0], dp[i-1][2] - prices[i])，注意买股票沿用的昨天不在冷冻期的状态，如果昨天进入了冷冻期那今天就不能买股票了。

- 状态1只有一种情况，也就是昨天持有股票今天卖了并进入冷冻期

dp[i][1] = dp[i-1][0] + prices[i]

- 状态2有两种情况，延续之前的不持有股票状态和刚从冷冻期解冻且不买股票。

dp[i][2] = max(dp[i-1][1], dp[i-1][2])

3. dp数组的初始化

只有状态0需要初始化为-prices[i]，因为状态0是第一天就持有股票。

4. 遍历顺序

递推公式中有i-1，所以从前往后遍历

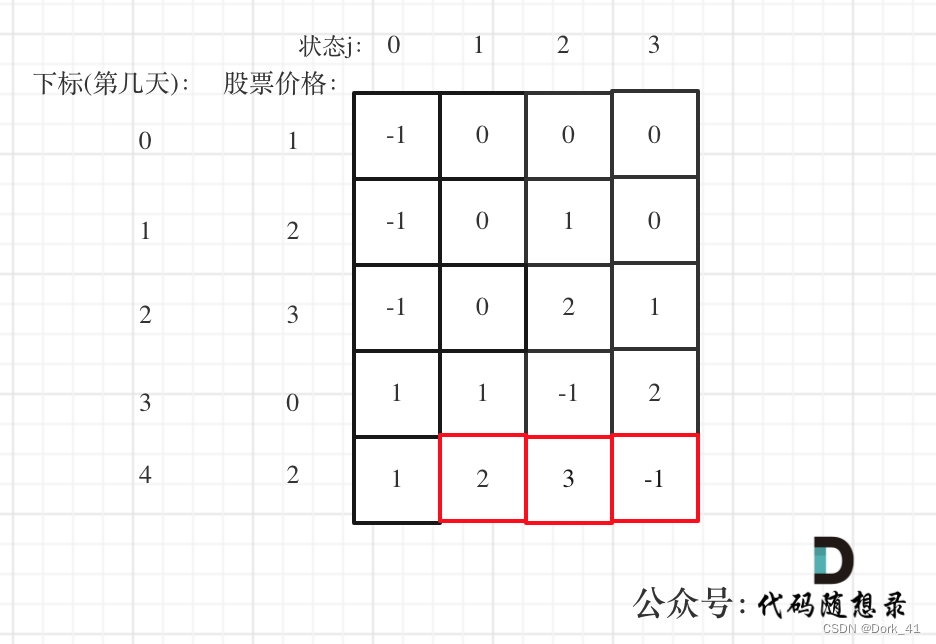
5. dp数组举例

714.买卖股票的最佳时机含手续费

class Solution:def maxProfit(self, prices: List[int], fee: int) -> int:if len(prices) == 0:return 0dp = [[0]*2 for _ in range(len(prices))]dp[0][0] = -prices[0]for i in range(1, len(prices)):dp[i][0] = max(dp[i-1][0], dp[i-1][1] - prices[i])dp[i][1] = max(dp[i-1][1], dp[i-1][0] + prices[i] - fee)return dp[-1][1]

• 时间复杂度：O(n)
• 空间复杂度：O(n)

和最常规的买卖股票题的唯一区别就是加了一个手续费，只有在卖出的时候减去手续费fee即可。

唯一差别在于递推公式部分，所以本篇也就不按照动规五部曲详细讲解了，主要讲解一下递推公式部分。

这里重申一下dp数组的含义：

dp[i][0] 表示第i天持有股票所省最多现金。 dp[i][1] 表示第i天不持有股票所得最多现金

如果第i天持有股票即dp[i][0]， 那么可以由两个状态推出来

• 第i-1天就持有股票，那么就保持现状，所得现金就是昨天持有股票的所得现金 即：dp[i - 1][0]
• 第i天买入股票，所得现金就是昨天不持有股票的所得现金减去 今天的股票价格 即：dp[i - 1][1] - prices[i]

所以：dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);

在来看看如果第i天不持有股票即dp[i][1]的情况， 依然可以由两个状态推出来

• 第i-1天就不持有股票，那么就保持现状，所得现金就是昨天不持有股票的所得现金 即：dp[i - 1][1]
• 第i天卖出股票，所得现金就是按照今天股票价格卖出后所得现金，注意这里需要有手续费了即：dp[i - 1][0] + prices[i] - fee

所以：dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i] - fee);

最后返回的是最后一天不持有股票时候的现金数。